“Una cuestión muy curiosa que ha desafiado la inteligencia de muchas personas, me inspiró para emprender la siguiente investigación que al parecer ha abierto una nueva trayectoria dentro del Análisis y, en particular, en Combinatoria. Esta cuestión concierne a un grupo de treinta y seis oficiales de seis rangos diferentes, tomados de seis regimientos distintos, y distribuidos en un cuadrado de tal forma que en cada fila y cada columna haya seis oficiales, cada uno de diferente rango y regimiento. Pero, después de dedicar muchos esfuerzos a resolver este problema, tenemos que reconocer que tal disposición es absolutamente imposible, aunque no podemos ofrecer una prueba rigurosa.”

Este es el primer párrafo del texto del matemático suizo Leonhard Euler (1707-1783) Recherches sur une nouvelle espece de quarres magiques (Investigaciones sobre un nuevo tipo de cuadrados mágicos), enviado a la Academia de San Petersburgo en 1779, y publicado por primera vez en la revista de la Sociedad Zeelandesa de Ciencias en Vlissingen, ciudad de la región de Zelanda en los Países Bajos, Verhandelingen uitgegeven door het zeeuwsch Genootschap der Wetenschappen te Vlissingen n. 9, 1782.

Primera página de la publicación de Leonhard Euler Recherches sur une nouvelle espece de quarres magiques, de 1782, y portada de la revista en la que aparece

Este es el conocido como problema de los treinta y seis oficiales de Euler, y que está relacionado con los cuadrados latinos que vimos en mi anterior entrega de la sección Matemoción del Cuaderno de Cultura Científica Cuadrados latinos, matemáticas y arte moderno, y más concretamente, con los llamados cuadrados greco-latinos que veremos en esta entrada.

Pero empecemos por el principio. Un cuadrado greco-latino de orden n es una matriz cuadrada de tamaño n x n en la cual cada entrada es un par ordenado de los números 1, 2, …, n, de forma que los dos cuadrados formados uno solo por las primeras entradas, y el otro solo por las segundas, son cuadrados latinos, y cada uno de los n² posibles pares aparece exactamente una vez en toda la matriz.

Los dos cuadrados latinos que forman un cuadrado greco-latino se dice que son cuadrados latinos ortogonales.

En lugar de números podemos utilizar otros símbolos, por ejemplo, considerar letras del alfabeto latino para las primeras entradas de los pares de números, que son los que forman el primer cuadrado latino, y letras del alfabeto griego para las segundas entradas, aquellos del segundo cuadrado latino. Así, la condición de que el retículo de pares de latinas y griegas sea un cuadrado greco-latino es que cada retículo parcial de letras latinas, y de letras griegas, sean cuadrados latinos, y que cada par de letras latina y griega aparezca una sola vez en toda la matriz. Como por ejemplo, el cuadrado greco-latino que aparece a continuación.

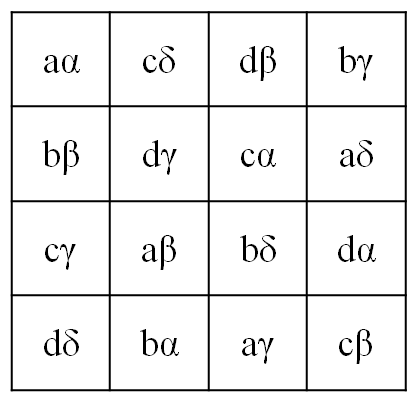
El nombre de cuadrados greco-latinos viene del hecho de que Leonhard Euler, quien introdujo y estudió estos objetos matemáticos, utilizó la notación de los alfabetos latino y griego para definirlos.

Aunque el matemático más prolífico de todos los tiempos, introdujo en 1776 los cuadrados greco-latinos, como un nuevo método para construir cuadrados mágicos, algunos ejemplos de estos ya habían aparecido con anterioridad. En 1725, el matemático francés Jacques Ozanam (1640-1718) incluye en su libro Récréations mathématiques et physiques el siguiente rompecabezas con cartas:

Colocar los reyes, reinas, jotas y ases de una baraja de cartas, formando un cuadrado 4 x 4, tal que cada fila y cada columna contenga una vez y solo una vez, cada una de las figuras y cada uno de los palos.

Y aquí convendría pararnos un momento. Si tenéis unas cartas a mano, este es un bonito problema para pasar un rato divertido intentando resolverlo. Lo podéis intentar en este mismo momento, o esperar a terminar de leer esta entrada sobre cuadrados latinos ortogonales.

Existen un total de 1152 soluciones a este problema con casi 300 años de antigüedad, que se resumen en las dos siguientes.

Las dos soluciones básicas al rompecabezas de las cartas

Para cada una de las dos soluciones, se pueden permutar las cuatro figuras (reyes, reinas, jotas y ases), y hay 4!=24 formas de hacerlo, y los cuatro palos (picas, corazones, diamantes o tréboles en las barajas francesa o inglesa, u oros, copas, espadas y bastos en la española), con otras 24 formas diferentes, luego cada una de las dos soluciones nos dará 24 x 24 = 576 soluciones.

Euler publicó dos trabajos sobre cuadrados greco-latinos, también llamados posteriormente cuadrados de Euler. En el primero De Quadratis Magicis (1776) utiliza cuadrados greco-latinos de órdenes 3, 4 y 5 para construir cuadrados mágicos (puede verse la entrada Habibi y los cuadrados mágicos I, y las dos siguientes, para más información sobre cuadrados mágicos), aunque para el orden 6 utiliza otro método que no tiene nada que ver con los cuadrados greco-latinos, y no es ninguna casualidad. La construcción es la siguiente. Se considera un cuadrado de Euler de orden n, y se reemplaza cada par de números ab por el número (a-1) n + b.

El segundo trabajo es el que ya hemos citado al principio de esta entrada, Recherches sur une nouvelle espece de quarres magiques (1782), que es el primer análisis matemático sobre cuadrados latinos ortogonales. El trabajo empieza, como ya hemos citado, con el conocido problema de los 36 oficiales: ¿Es posible colocar 36 oficiales de 6 rangos distintos y de 6 regimientos diferentes en una formación cuadrada (es decir, formando un cuadrado 6×6) de forma que en cada fila y cada columna haya seis oficiales, cada uno de un rango y un regimiento diferentes?. Evidentemente, la solución al problema de los 36 oficiales, de existir, es un cuadrado de Euler de orden 6, donde los símbolos serían los rangos y los regimientos.

El matemático de Basilea estudió en este trabajo métodos para construir cuadrados greco-latinos completando un cuadrado latino inicial. Empieza considerando “cuadrados latinos de un paso” (que son aquellos cuadrados latinos que se construyen de la siguiente manera, en la primera fila se colocan los números en su orden creciente natural 1, 2, 3, …, n, y en cada una de las demás filas se va rotando una posición, así en la segunda fila las entradas son 2, 3,…, n, 1, en la tercer fila, 3, 4, …, n, 1, 2, así hasta la última fila, n, 1, 2, …, n-1), los completa para los órdenes 3, 5, 7 y 9, pero demuestra que no se pueden completar para los órdenes pares.

A continuación, veamos la demostración original, del matemático que con 19 años publicó su primera memoria científica (enviada a la Academia de París) sobre la distribución óptima de mástiles y velas en los barcos, a pesar de que nunca había visto un barco de vela, sobre el hecho de que no se pueden completar cuadrados latinos de un paso para los órdenes pares.

Demostración. Considérese el cuadrado latino de un paso de orden n, que va a intentar completarse para formar un cuadrado greco-latino. Sin pérdida de generalidad, puede suponerse que la primera casilla del cuadrado greco-latino es 11. Si se ha completado el cuadrado latino, existirá lo que Euler llamaba una “fórmula guía” para el número 1 (1, a, b, c, d, e,…) que enumera las columnas en las que se encuentran los 1s de las segundas entradas según se van considerando las diferentes filas. Así, la fórmula guía del segundo cuadrado de Euler de orden 5 de la imagen anterior es (1, 3, 5, 2, 4). Y considérense ahora las primeras entradas que acompañan a esos 1s que están en la segunda entrada, (1, , , , ,…), que en el ejemplo anterior sería (1, 4, 2, 5, 3).

La situación se describe gráficamente en la siguiente imagen.

Como el número 1, siendo segunda entrada, recorre todas las columnas, y las primeras entradas que lo acompañan recorren todos los números de 1 a n, entonces

Pero partimos de un cuadrado latino de un paso. Como la primera entrada de la casilla de la segunda fila y columna a es , y en cada fila se rota cíclicamente, con paso uno, la disposición de la fila anterior, entonces será igual a (a+1), módulo n (esto se debe a que la rotación es cíclica y al llegar a la columna n se sigue por la primera columna, esto es, . Por lo tanto,

Lo mismo ocurre para el resto de primeras entradas con segunda entrada 1, así

Introduciendo esta información en la igualdad anterior, se obtiene que

Y haciendo uso de la fórmula de la suma de los primeros números naturales,

,

se observa que esta cantidad tiene que ser múltiplo de n, lo cual solamente puede ocurrir si n es impar. QED

Trivialmente, no existen cuadrados latinos ortogonales de orden 2, puesto que los únicos cuadrados latinos de orden 2,

no son ortogonales. Los pares 12 y 21 se repetirían en el cuadrado. Sí existen cuadrados latinos ortogonales de orden 4 como se ha visto anteriormente en esta entrada.

Además, el matemático responsable de la fórmula más hermosa de las matemáticas, obtiene otras evidencias de que no existen tampoco cuadrados greco-latinos de orden 6. Tras su estudio sobre el completado de cuadrados latinos de paso uno, estudia el caso de los “cuadrados latinos de múltiples pasos”. Para un divisor m de n (el orden del cuadrado latino), se define el cuadrado latino de paso m como aquel en el que se hace una partición del cuadrado n x n en bloques m x m, cada uno de los cuales es un cuadrado latino de paso uno, y además los bloques se van rotando cíclicamente con paso 1.

El autor del texto Recherches sur une nouvelle espece de quarres magiques demostró en él que los cuadrados latinos de orden 6 de múltiples pasos (que son los que están relacionados con el problema de los 36 oficiales) no se pueden completar.

En general, demostró la existencia de cuadrados greco-latinos para todos los órdenes distintos de 4k+2. Y las evidencias que tenía sobre el orden 6 le llevaron a conjeturar que de hecho no existen cuadrados latinos ortogonales para los órdenes 6, 10, 14,… es decir, de la forma 4k+2.

En 1901, el matemático amateur francés Gaston Tarry demostró (en su artículo Le problème des 36 officiers, Comptes Rendus Assoc. France Av. Sci. 29, n. 2, 1900) que la conjetura de Euler era cierta para el orden 6, mediante el laborioso trabajo de listar todos los cuadrados latinos de orden 6 (y recordemos que hay 812.851.200) y ver que no hay dos de ellos que sean ortogonales, aunque redujo su estudio a 9.408 casos.

En el artículo Graeco-Latin Squares and a Mistaken Conjecture of Euler, Dominic Klyve y Lee Stemkoski comentan que la primera demostración de la no existencia de cuadrados latinos ortogonales, y por lo tanto, de que el problema de los 36 oficiales de Euler no tiene solución, podría deberse al matemático y astrónomo danés Thomas Clausen (1801-1885). Este trabajó como asistente del astrónomo Heinrich Ch. Schumacher (1780-1850) en el Observatorio de Altona (Alemania), quien en una carta al matemático Carl Friedrich Gauss (1777-1855), entonces en el Observatorio de Gotinga, le comenta que Clausen ha demostrado la no existencia de cuadrados latinos ortogonales de orden 6. Por desgracia la mayoría de los trabajos científicos de Clausen (alrededor de 150) se han perdido, y no hay ningún registro de su demostración.

Hoy en día existen demostraciones más cortas y elegantes que la de Tarry, cada una de ellas utilizando técnicas de áreas muy distintas, como geometría proyectiva, teoría de códigos algebraica, o teoría de grafos. Algunos ejemplos:

H. Bruck, H. J. Ryser, The non-existence of certain finite projective planes, Canad. J. Mathematics 1, p. 88-93, 1949.

Z. Lie, A short disproof of Euler’s conjecture concerning orthogonal Latin squares, Ars Combinatoria 14, p. 47–55, 1982.

D. R. Stinson, A short proof of the nonexistence of a pair of orthogonal Latin squares of order six, Journal Combinatorial Theory Ser. A 36, p. 373–376, 1984.

Steven T. Dougherty, A coding theoretic solution to the 36 officer problem, Designs, Codes and Cryptography 4, p. 123-128, 1994.

Tras la demostración de G. Tarry de la conjetura de Euler para orden 6, aún quedaba abierta la conjetura para los órdenes superiores, 10, 14, 18, 22, etc. Sin embargo, en 1959, R. C. Bose y S. S. Shrikhande construyeron un cuadrado greco-latino de orden 22, el primer contraejemplo a la conjetura de Euler, y E. T. Parker un contraejemplo de orden 10, el más pequeño posible.

De hecho, la conjetura de Euler es falsa para todos los órdenes 4k+2 ≥ 10, como demostraron los tres matemáticos en el artículo conjunto Further results on the construction of mutually orthogonal Latin squares and the falsity of Euler’s conjecture (Canadian Journal of Mathematics 12, 1960).

Este trabajo se enmarca dentro del estudio de los cuadrados latinos mutuamente ortogonales. Un conjunto de m cuadrados latinos L₁, L₂, …, L_m de orden n se dice que son mutuamente ortogonales si son ortogonales dos a dos.

Para terminar, la existencia de cuadrados greco-latinos de orden 10 que refutaban la conjetura Euler llegó también al mundo de la literatura. El escritor oulipiano George Perec hizo uso de un cuadrado de Euler de orden 10 en la estructura de su novela La vida instrucciones de uso (Anagrama, 1992), escrita durante los años 1976 y 1978. En el excelente artículo La vida instrucciones de uso, de George Perec de mi colega y amiga Marta Macho para la sección de Literatura y Matemáticas del portal divulgamat, podéis encontrar la explicación del uso del cuadrado greco-latino de orden 10, así como de otras estructuras matemáticas.

Bibliografía

1.- Leonhard Euler, Recherches sur une nouvelle espece de quarres magiques (Investigaciones sobre un nuevo tipo de cuadrados mágicos), 1779.

2.- VVAA., El rostro humano de las matemáticas, Nivola, 2008.

3.- L. D. Andersen, Chapter on The history of latin squares, Department of Mathematical Sciences, Aalborg University. (Research Report Series; No. R-2007-32), 2007.

4.- Leonhard Euler, De Quadratis magicis (Sobre cuadrados mágicos), 1776.

5.- Dominic Klyve, Lee Stemkoski, Graeco-Latin Squares and a Mistaken Conjecture of Euler, College Mathematical Journal 37, 2006.

6.- Peter J. Cameron, Notes on Combinatorics

7.- Gaston Tarry, Le problème des 36 officiers, Comptes Rendus Assoc. France Av. Sci. 29, n. 2, 1900.

8.- H. Bruck, H. J. Ryser, The non-existence of certain finite projective planes, Canad. J. Mathematics 1, p. 88-93, 1949.

9.- Z. Lie, A short disproof of Euler’s conjecture concerning orthogonal Latin squares, Ars Combinatoria 14, p. 47–55, 1982.

10.- D. R. Stinson, A short proof of the nonexistence of a pair of orthogonal Latin squares of order six, Journal Combinatorial Theory Ser. A 36, p. 373–376, 1984.

11.- Steven T. Dougherty, A coding theoretic solution to the 36 officer problem, Designs, Codes and Cryptography 4, p. 123-128, 1994.

12.- R. C. Bose, S. S. Shrikhande, E. T. Parker, Further results on the construction of mutually orthogonal Latin squares and the falsity of Euler’s conjecture, Canadian Journal of Mathematics 12, p. 189-203, 1960.

13.- Marta Macho, La vida instrucciones de uso, de George Perec

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica