Mis primeras entradas en el Cuaderno de Cultura Científica estuvieron dedicadas a unos objetos matemáticos muy interesantes, que se utilizaron en la antigüedad como amuletos y talismanes, los cuadrados mágicos:
1.- Habibi y los cuadrados mágicos I
2.- Habibi y los cuadrados mágicos II
3.- Habibi y los cuadrados mágicos III
La entrada de hoy la vamos a dedicar a otros objetos matemáticos similares, que también fueron utilizados en la antigüedad como amuletos, los cuadrados latinos.

Un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n (aunque bien podrían considerarse n símbolos cualesquiera, por ejemplo, las letras del alfabeto latino que utilizó el matemático suizo Leonhard Euler o los colores utilizados por Lohse), de tal forma que cada número de {1,…, n} aparece una vez, y sólo una vez, en cada fila y cada columna.

El origen de los cuadrados latinos se remonta por lo menos a los alrededores del año 1.000 en los que las comunidades árabe e india los utilizaban, junto a los cuadrados mágicos, como amuletos o talismanes. Aunque eran los cuadrados mágicos los diseños numéricos cuadrados que eran más habituales y desde mucho tiempo antes (véase Habibi y los cuadrados mágicos), también se utilizaron cuadrados latinos, y con un uso similar, “se les relacionaba con los planetas y con la alquimia, con la magia y la astrología, con la numerología, y también se utilizaban para sanar o como amuletos”, para combatir a los demonios o reverenciar a los dioses.
Los primeros cuadrados latinos que aparecen en una publicación son, que sepamos, los contenidos en el libro del sufí, escritor esotérico y matemático árabe Ahmad al-Buni (murió en el 1225), “Shams al-Ma’arif al-Kubra”(El sol del gran conocimiento), quien se interesó por sus poderes mágicos como talismanes, por su valor místico, construyó cuadrados latinos 4 x 4 con las letras de uno de los 99 nombres de Alá, y, desde un punto de vista matemático, como herramientas para construir cuadrados mágicos.
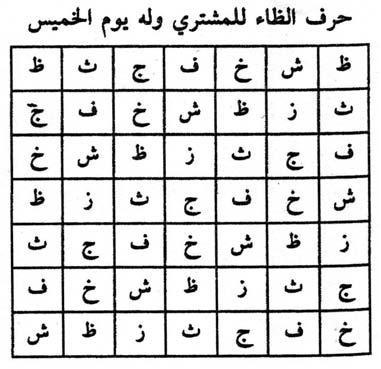
Por otra parte, en el siglo XIII, el filósofo y escritor mallorquín Ramón Llull (1232-1315) construye en su texto Ars Demostrativa (1283) cuatro cuadrados latinos de orden 4, cuyos símbolos eran fuego, aire, agua y tierra, en sus esfuerzos por explicar el mundo mediante métodos combinatorios.

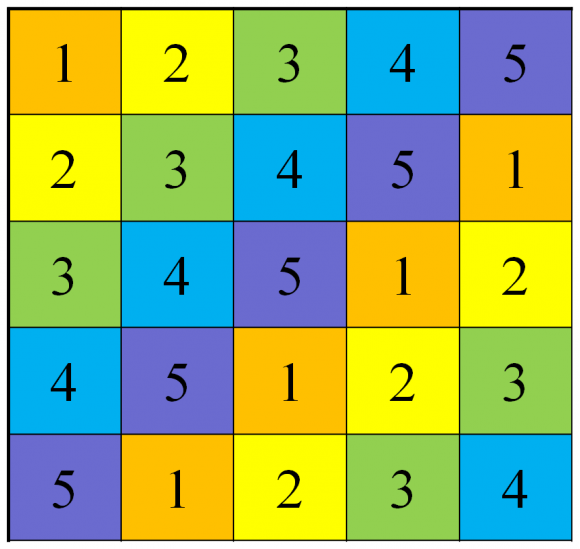
Pero volviendo a los cuadrados latinos, se observa fácilmente que existe al menos un cuadrado latino para cada orden n, sin más que poner los números 1, 2,…, n en la primera fila y luego ir rotando cíclicamente en las siguientes.
Ejemplos de cuadrados latinos aparecen en álgebra, puesto que las “tablas de Cayley” asociadas a los grupos finitos son cuadrados latinos de orden igual al número de elementos del grupo, y cuyos símbolos son los elementos del grupo.
Como todos sabéis los grupos son estructuras algebraicas muy importantes en matemáticas, y con importantes aplicaciones en física, química, astrofísica, criptografía, cristalografía e incluso en la creación y análisis de juegos, como el cubo de Rubik.
Recordemos su definición. Un grupo es un conjunto, llamémosle G, con una operación *, de modo que a partir de dos elementos a y b del conjunto G, nos da un nuevo elemento, a*b, del conjunto G, y tal que dicha operación verifica una serie de axiomas:
i) propiedad asociativa, a*(b*c) = (a*b)*c, para todos los elementos a, b y c de G;
ii) elemento identidad, existe un elemento e de G tal que a*e = a = e*a;
iii) elemento inverso, para cada elemento a de G, existe un elemento b (llamado inverso, y que suele denotarse como a-1) tal que a*b = e = b*a. Los grupos son abelianos si se cumple la propiedad conmutativa, es decir, si para cualesquiera elementos a y b de G, a*b = b*a, pero no todos los grupos son abelianos.
El matemático inglés Arthur Cayley (1821-1895) describía la estructura de los grupos finitos (es decir, con un número finito de elementos) mediante la tabla de los productos de los elementos del grupo, la llamada tabla de Cayley, en la que se colocan a la izquierda y arriba de la tabla los elementos del grupo y en las casillas correspondientes (como en el juego de los barcos) se sitúa el producto de los mismos.

Las propiedades del grupo hacen que la tabla de Cayley de los grupos finitos sean cuadrados latinos de orden igual al número de elementos del grupo. Si G = {g1,g2,…,gn} y si en una fila, por ejemplo, la del producto del elemento gk apareciese un mismo elemento en dos entradas (que es lo que ocurriría si no fuese un cuadrado latino), entonces existirían dos elementos distintos del grupo, gi y gj, tal que gk*gi = gk*gj (los valores de las dos entradas), y multiplicando por la izquierda por el inverso de gk, tendríamos que gi = gj, lo cual no es posible ya que los elementos gi y gj son distintos. Y lo mismo para las columnas.
![Ejemplos de cuadrados latinos de ordenes 2, 3 y 4 asociados a los grupos finitos siguientes: el grupo cíclico binario 2, el grupo cíclico de orden 3, 3, y el grupo de Cayley 2 x 2. Recordemos que el grupo cíclico de orden n, n, es el grupo formado por los números enteros módulo n, es decir, al llegar a n-1, volvemos a empezar por 0, [n] = [0], [n+1]=[1], etc. n = {g1 = [0], g2 = [1], …, gn = [n-1]}, con la operación aditiva +, por ejemplo, en 5, [2] + [2] = [4], [1] + [4] = [0], [4] + [3] = [2], etc. Además, la base del grupo de Cayley es {g1 = ([0],[0]), g2 = ([0],[1]), g3 = ([1],[0]), g4 = ([1],[1])}](https://culturacientifica.com/app/uploads/2015/01/imagen-7-580x238.png)
De hecho, los cuadrados latinos generalizan el concepto de grupo, y un conjunto finito G con una operación * se dice que es un cuasi grupo si su tabla de Cayley es un cuadrado latino. Para un conjunto G, no necesariamente finito, la propiedad definitoria es que para cada par de elementos a y b de G existen dos elementos únicos x e y tales que a * x = b, y * a = b (que es la condición que generaliza la condición de cuadrado latino).
Una cuestión interesante es conocer cual el número de cuadrados latinos que existen para cada orden n, L(n). Se puede demostrar que una cota inferior a ese número L(n) es la siguiente.
Teorema: El número de cuadrados latinos de orden n, L(n), es al menos n! (n-1)!… 3! 2! 1!.
Para este resultado necesitamos recordar qué es el factorial de un número y cuál es su significado. Dado un número k se define como k! = k.(k-1)…3.2.1. Esta operación matemática nos expresa las formas distintas en las que se pueden ordenar un conjunto de n elementos, es decir, las posibles permutaciones de k números, o de k elementos, es decir las formas de ordenarlos. Veamos un ejemplo.
La novela “Tangram” del bilbaíno Juan Carlos Márquez (Premio Euskadi de Literatura 2012) está compuesta por 7 relatos (tantos como piezas del Tangram, como ya comentamos en la entrada del Cuaderno de Cultura Científica, “Tangram”), que están conectados entre sí, pero que se pueden leer de forma independiente y en cualquier orden. Por lo tanto, ¿de cuantas formas podemos leer los 7 relatos que componen la novela “Tangram”? El problema matemático es de cuántas formas podemos ordenar 7 elementos.
Para empezar tenemos que fijar el primer relato en ser leído, y tenemos 7 posibilidades, cada uno de los siete relatos escritos por Márquez. Una vez fijado el primer relato en ser leído, como segunda lectura tenemos solamente 6 posibles relatos, los 7 que había menos el que va a ser leído en primer lugar. Por lo que, por ahora, tenemos 7 x 6 = 42 posibilidades distintas de lectura de los dos primeros relatos. Sigamos. Para tercera lectura tenemos 5 posibles relatos (los que aún no hemos leído), entonces, tenemos 7 x 6 x 5 = 210 posibilidades distintas de lectura de los tres primeros relatos. Y así podemos seguir hasta el final, tendremos 4 posibles relatos como cuarta lectura, 3 para la quinta, 2 para la sexta y finalmente, solo nos quedará una opción como último relato. En consecuencia, el número de posibles lecturas de los 7 relatos de la novela “Tangram”, si los podemos leer en cualquier orden, son el factorial de 7, 7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5.040.

Ahora, la demostración del teorema anterior, aunque sin todo el rigor matemático necesario, consiste en la siguiente idea. Para construir un cuadrado latino de orden n podríamos empezar con una primera fila con los n símbolos, los números 1, 2,…, n, y hay n! formas de colocar los n números en esa primera fila, es decir, todas las posibles permutaciones de esos n números.

Fijada una de esas permutaciones para la primera fila, podríamos pasar a rellenar la segunda fila. La idea es la misma que para la primera fila, pero manteniendo además que columna a columna tampoco se pueden repetir los números. Es decir, a la hora de elegir el número de cada casilla, no puede coincidir con los que ya hemos puesto en esa fila, como en el razonamiento anterior de los relatos de Márquez, pero tampoco con los números fijados en la columna en la que está. Por ejemplo, en el ejemplo de la imagen, en la primera casilla solo tenemos 3 opciones (1, 2 o 4), y no 4 como en la primera fila. En consecuencia, hay (n-1)! posibles distribuciones de los números para la segunda fila. De igual forma, (n-2)! para la tercera, y así hasta la última. En total, n! (n-1)!… 3! 2! 1!.
Otra forma de acercarnos al cálculo del número de cuadrados latinos es limitar su búsqueda a los cuadrados latinos reducidos, que son aquellos para los que la primera fila y la primera columna son 1, 2, 3, …, n, como por ejemplo el cuadrado latino de orden 5 anterior.
Si cogemos todos los cuadrados latinos reducidos, podemos obtener el resto de cuadrados latinos de la siguiente forma. Permutamos las n columnas de cada cuadrado latino reducido, lo cual nos genera nuevos cuadrados latinos todos ellos distintos, exactamente n! que es el número de permutaciones posibles, y si ahora a todos estos nuevos cuadrados latinos les permutamos todas las filas menos la primera, n-1 filas, obtendríamos más cuadrados latinos distintos (si permutásemos también la primera se generarían cuadrados latinos que ya han aparecido; pensemos en el caso de los cuadrados latinos de orden 2, hay uno reducido y el otro no reducido, si tomamos el reducido y permutamos la filas se obtiene el no reducido, pero si ahora le permutamos a este las columnas volvemos a obtener el cuadrado latino reducido). Por lo tanto, si denotamos por l(n) el número de cuadrados latinos reducidos de orden, entonces
L(n) = n! (n-1)! l(n).
No es difícil de calcular que hay cuatro cuadrados latinos reducidos de orden 4 (os lo dejo como divertimento), por lo que hay 4! x 3! X 4 = 576 cuadrados latinos de orden 4.
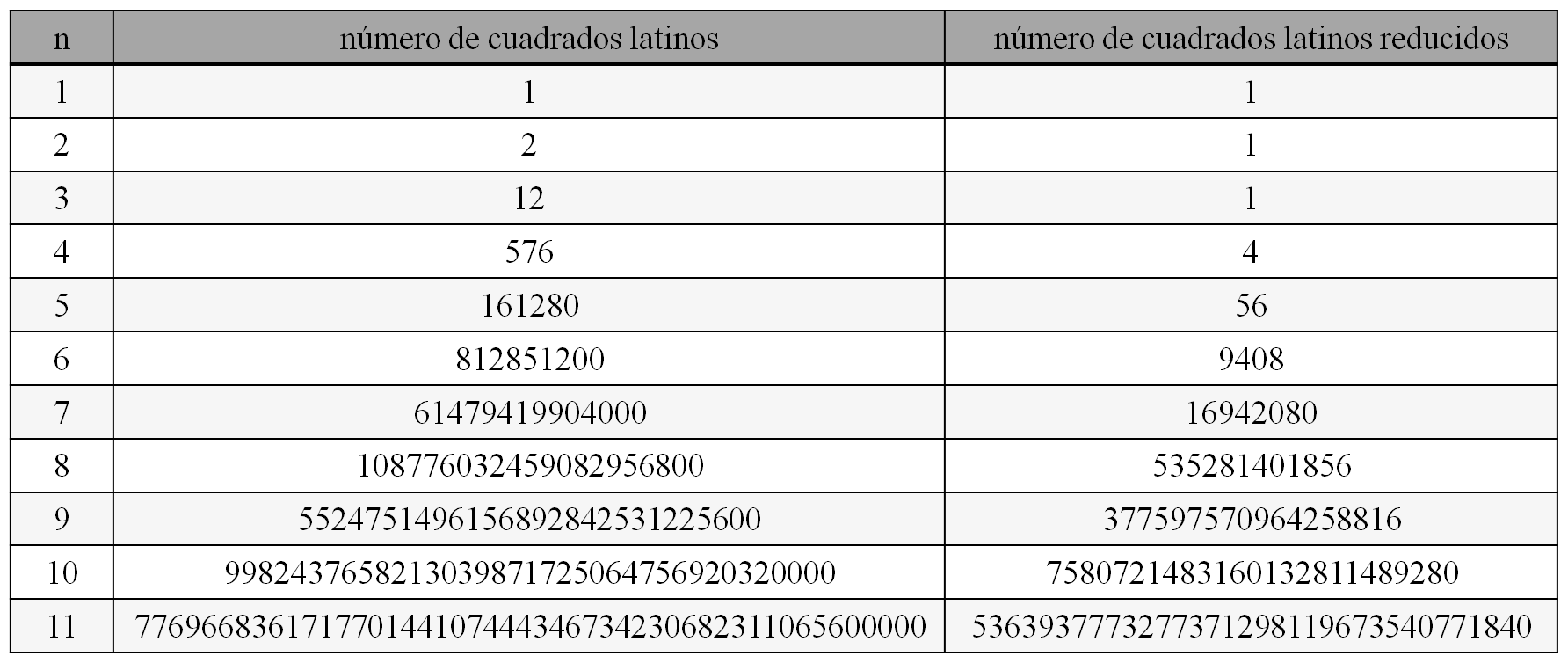
El cálculo de L(n) y l(n) es realmente complejo. En el artículo de el artículo de McKay, Meynert y Myrvold se han calculado hasta el orden 11.

Los cuadrados latinos, y sus familiares, los cuadrados greco-latinos (de los que hablaremos en otra entrada), tienen interesantes aplicaciones en estadística (en el diseño de experimentos), en álgebra, en teoría de la información (en códigos correctores de errores), en criptografía, en geometría proyectiva, o en juegos matemáticos. Veamos un sencillo ejemplo de su utilización en el diseño de experimentos estadísticos.

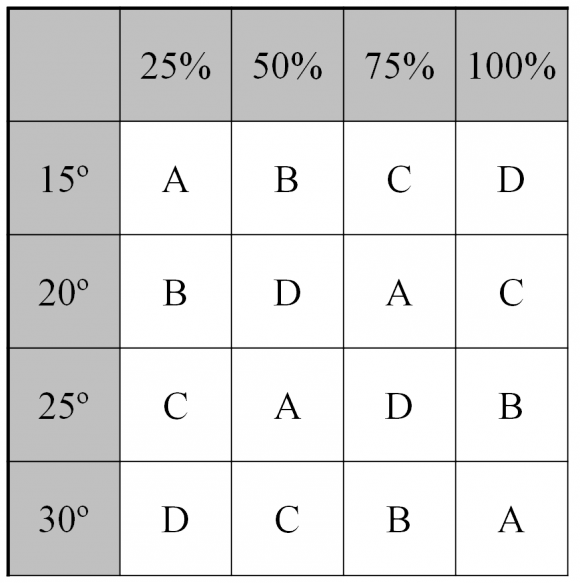
Imaginemos que queremos estudiar el comportamiento de cuatro fertilizantes, llamémosles A, B, C y D, sobre el cultivo de una cierta planta en un invernadero, en diferentes condiciones de luz y temperatura, por ejemplo, con un 25%, 50%, 75% y 100% de exposición a la luz del sol, y a 15º, 20º, 25º y 30º de temperatura. Entonces montamos una estructura reticular cuadrada en el invernadero, en la que cada fila se corresponde con una exposición diferente a la luz del sol y cada columna con una temperatura distinta. Para el diseño del experimento estadístico se disponen los fertilizantes siguiendo un diseño de cuadrado latino (por ejemplo el que aparece en la siguiente imagen) para que en cada temperatura, y también para cada exposición al sol, se utilice uno y solo uno de los fertilizantes.
Como hemos visto al inicio de la entrada, los cuadrados latinos también aparecen en el arte moderno, en concreto son una fuente de inspiración para uno de los artistas cuyo arte se enmarca dentro del constructivismo y el arte concreto, el pintor y artista gráfico suizo Richard Paul Lohse (1902-1988).
Lohse pinta series de estructuras reticulares de cuadrados y rectángulos en las cuales el estudio del color es una parte fundamental. En algunas de sus obras utiliza el concepto de cuadrado latino, como en las siguientes obras, similares a la primera mostrada en esta entrada.
El primer cuadro “Composición para Bossin” comparte el cuadrado latino de la primera imagen de la entrada, pero no así el segundo cuadro, “Seis rangos de color sistemáticos” (1950 y 1972).
En otra serie de cuadros juega a modificar la estructura perfectamente cuadrada de las celdillas convirtiéndolas en rectángulos de diferentes dimensiones, y además considerando cuadrados latinos, de colores, de órdenes mayores o iguales que 6.
“Seis líneas de color verticales sistemáticas con cuadrado amarillo” (1968), con cuadrado latino de orden 6, y “Nueve secuencias de color sistemáticas verticales incrementando la densidad” (1955 y1969), con cuadrado latino de orden 9.


Pero además, a partir de los cuadrados latinos del artista Richard P. Lohse se ha introducido en matemáticas un nuevo concepto de estructura algebraica, los grupos con la propiedad de Lohse. En el artículo “On groups with the Lohse property” se introducen y estudian los grupos con la propiedad de Lohse, que son grupos finitos para los cuales la correspondiente tabla de Cayley está inspirada en las citadas obras del artista co-fundador del grupo Allianz que reunía a artistas “concretistas” suizos, en las cuales la celdilla de cada color está aislada de celdillas del mismo color en todas las direcciones (véanse los anteriores cuadros). Por lo tanto, un grupo finito se dice que tiene la propiedad de Lohse si su tabla de Cayley, que además es un cuadrado latino, satisface la propiedad de que cada entrada es diferente de las entradas diagonalmente adyacentes.

Bibliografía
1.- Cuaderno de Cultura Científica: Habibi y los cuadrados mágicos I; Habibi y los cuadrados mágicos II; Habibi y los cuadrados mágicos III.
2.- L. D. Andersen, Chapter on The history of latin squares, Department of Mathematical Sciences, Aalborg University. (Research Report Series; No. R-2007-32), 2007.
3.- ¿Quién es Ramón Llull? Centre de Documentació Ramón Llull
4.- Cuaderno de Cultura Científica: Tangram
5.- Peter J. Cameron, Notes on Combinatorics
6.- Charles F. Laywine, Gary L. Mullen, Discrete mathematics using latin squares, John Wiley and sons, 1998.
7.- Juan Carlos Márquez, Tangram, Salto de Página, 2012.
8.- B. D. McKay, A. Meynert and W. Myrvold, Small Latin squares, quasigroups and loops, J. Combinatorial Designs, 15 (2007) 98-119.
10.- David Meier, On groups with the Lohse property, European Journal of Combinatorics 27, p. 1042-1053, 2006.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Esta entrada participa en la XII Edición delCarnaval de Humanidades, cuyo blog anfitrión es::ZTFNews.




Cuadrados latinos, matemáticas y arte ab…
[…] Mis primeras entradas en el Cuaderno de Cultura Científica estuvieron dedicadas a unos objetos matemáticos muy interesantes, que se utilizaron en la antigüedad como amuletos y talismanes, los cuadrados mágicos: 1.- Habibi y los… […]
Participaciones en la XII Edición del Carnaval de Humanidades | :: ZTFNews.org
[…] Cuadrados latinos, matemáticas y arte abstracto por Raúl Ibáñez participa desde el blog Cuaderno de Cultura […]
Pastranec
Esto me ha recordado a cómo se hacen los torneos de rondas en ajedrez, para asegurarse de que todos juegan contra todos, y además unas veces con blancas y otras con negras.
http://enciclopedia.us.es/index.php/Sistema_de_rondas_%28Ajedrez%29
RLl
Interesante artículo.
Una precisión: Ramón Llull era mallorquín, no catalán.
Raúl Ibáñez
Muchas gracias,
Y gracias por la corrección.
Un abrazo, Raúl.
Hitos en la red #51 – Naukas
[…] tipo de cosas hace que disfrutar de Cuadrados latinos, matemáticas y arte abstracto por Raúl Ibáñez, considerar cómo podríamos educar mejor a nuestros hijos en Los nórdicos no […]
Los cuadrados greco-latinos de Leonhard Euler | Matemoción | Cuaderno de Cultura Científica
[…] que vimos en mi anterior entrega de la sección Matemoción del Cuaderno de Cultura Científica Cuadrados latinos, matemáticas y arte moderno, y más concretamente, con los llamados cuadrados greco-latinos que veremos en esta […]
Resumen de la XII Edición del Carnaval de Humanidades | :: ZTFNews.org
[…] Cuadrados latinos, matemáticas y arte abstracto por Raúl Ibáñez participa desde el blog Cuaderno de Cultura […]
La ratonera, el juego de Cayley – Cuaderno de Cultura Científica
[…] n, n! = n ∙ (n – 1) ∙ (n – 2) ∙∙∙ 2 ∙ 1, como se vio, por ejemplo, en el artículo Cuadrados latinos, matemáticas y arte abstracto) se dan las siguientes […]
angel Pimentel
Muy bueno, lo de la foto del ensayo de arboles.
Una vez buscando para preparar mi clase la encontré. Ahora la puse como icono en un grupo de biometria en wassap.
En relación al ejemplo q ilustran sobre ka temperatura y luz, supongo q estos no son factores de interés, sino gradientes a controlar; ya q debe haber independencia entre fila, columna y tratamiento. Si lo hubiera, habría q considerar la integración entre factores, y el diseño sería otro…
El puzle Stomachion y el palimpsesto de Arquímedes (2) — Cuaderno de Cultura Científica
[…] de la combinatoria el contar cuántos cuadrados latinos existen de un orden dado (véase la entrada Cuadrados latinos, arte y matemáticas), cuántas soluciones tiene una ecuación lineal (véase Aprendiendo técnicas de contar: lotería […]
Arte Moebius (I) — Cuaderno de Cultura Científica
[…] – Cuadrados latinos, matemáticas y arte abstracto […]
Rompecabezas matemáticos con números — Cuaderno de Cultura Científica
[…] fila, columna o región. El sudoku está relacionado con los cuadrados latinos (véase la entrada Cuadrados latinos, matemáticas y arte abstracto o el libro Del ajedrez a los grafos, la seriedad matemática de los juegos) estudiados por el […]
Sudokus, matemáticas y arte contemporáneo — Cuaderno de Cultura Científica
[…] Recordemos que un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n, aunque bien podrían considerarse n símbolos cualesquiera, por ejemplo, las letras del alfabeto latino que utilizó el matemático suizo Leonhard Euler (1707-1783) o los colores utilizados por el artista suizo Richard Paul Lohse (1902-1988), de tal forma que cada número de {1,…, n} aparece una vez, y solo una vez, en cada fila y cada columna (parta más información véase la entrada Cuadrados latinos, matemáticas y arte abstracto). […]