En la segunda parte de esta anotación dedicada a los cuadrados mágicos, dejaremos por un momento de lado los aspectos mágico-misteriosos y la magistral novela de Craig Thompson y nos adentraremos un poco en las matemáticas de los cuadrados mágicos.
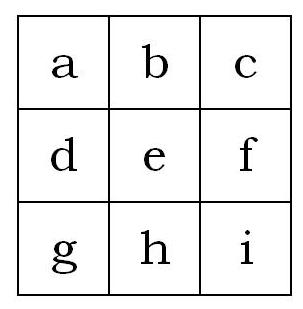
Ya sabemos que hay cuadrados mágicos de orden 3×3, pero es interesante plantearse además ¿cuántos hay? Esta cuestión se puede abordar desde un punto de vista puramente algebraico. Es decir, asignamos una incógnita a cada una de las entradas del cuadrado 3×3, como se muestra en la imagen
y consideramos las ecuaciones que surgen al considerar las condiciones de que la suma de los elementos de cada fila, de cada columna y cada diagonal da siempre 15. Las ecuaciones que quedan son
a + b + c = 15, d + e + f = 15, g +h + i = 15,
a + d + g = 15, b + e + h = 15, c + f + i = 15,
a + e + i = 15, g + e + c = 15.
Manipulando algebraicamente estas ecuaciones se llega fácilmente a que el número del centro “e” vale siempre 5, que curiosamente es el número que está en el medio de los nueve primeros números 1, 2, 3, 4, 5, 6, 7, 8, 9. Esta es una propiedad que van a compartir todos los cuadrados mágicos de orden impar, es decir, que en el centro está siempre “el número del medio”. Así, en un cuadrado mágico de orden 5, en el que se introducen los 25 primeros números, el número del centro será el número 13.
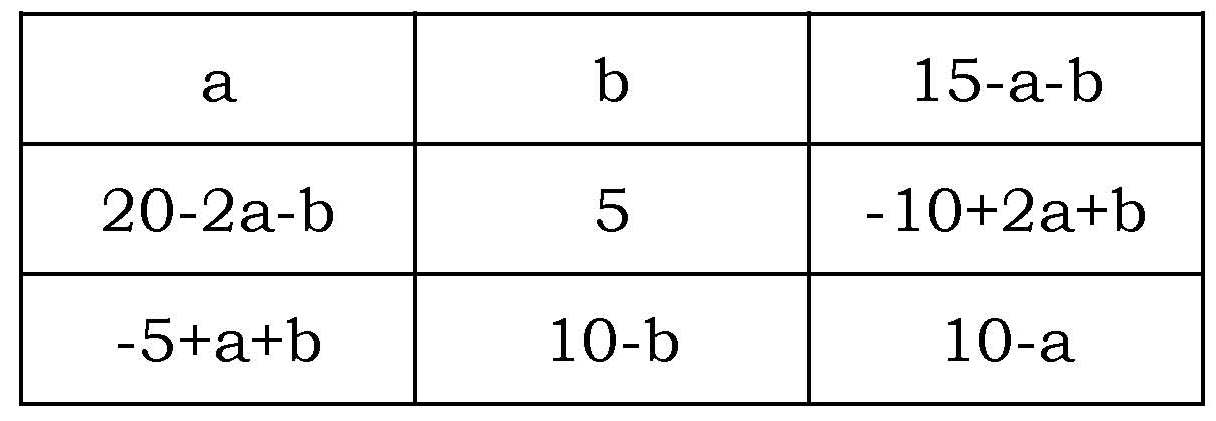
La segunda conclusión de las ecuaciones anteriores es que el cuadrado mágico es de la forma
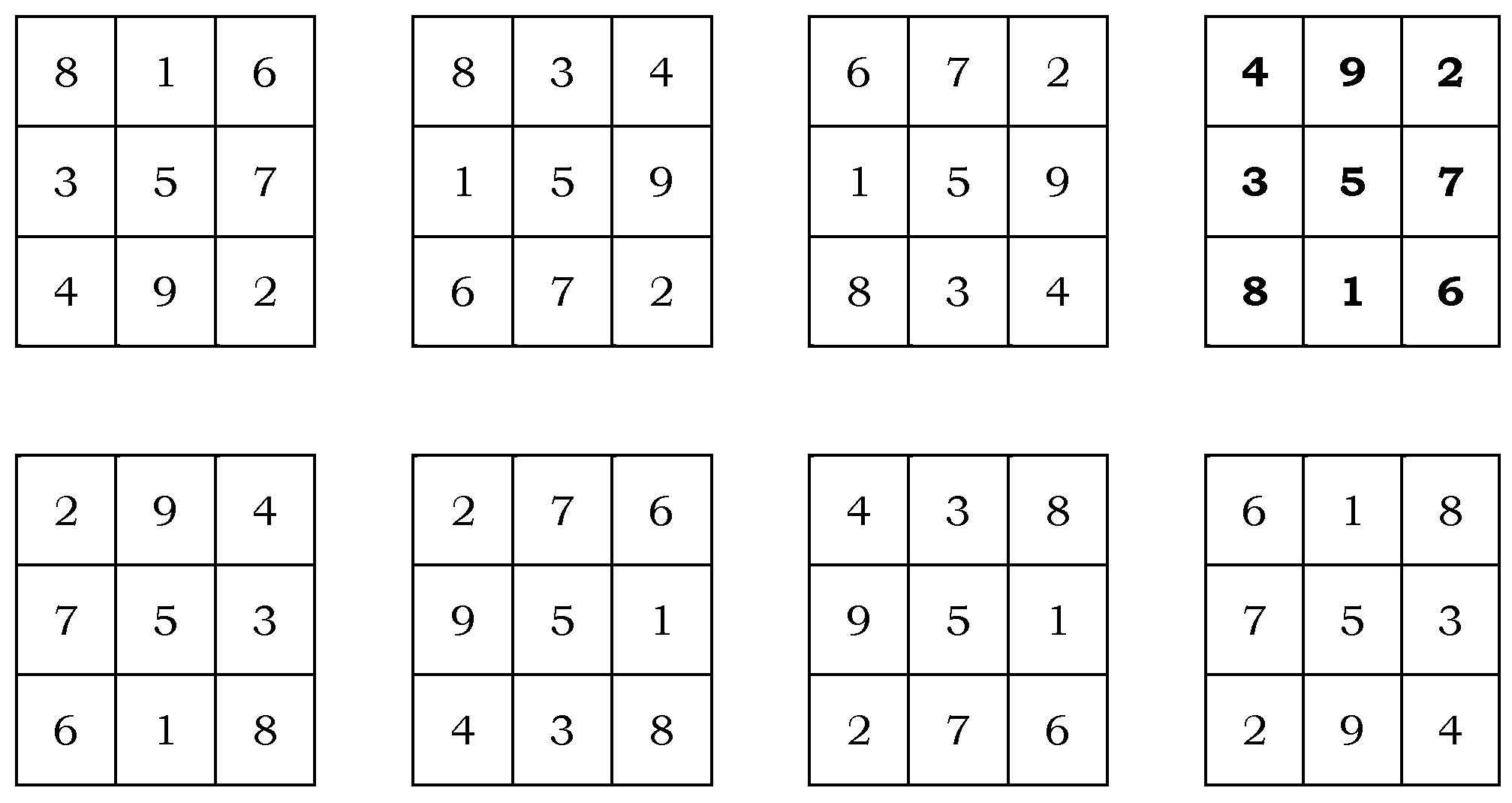
Dando a “a” y “b” valores entre 1 y 9, y viendo en qué casos se obtienen siempre números entre 1 y 9 para todas las entradas del cuadrado (por ejemplo, a = 1 no es posible ya que entonces 20 – 2a – b = 18 – b, que es mayor que 9), se llega finalmente a todas las posibles soluciones, que resulta que son ocho. A saber,
Si nos fijamos un poco en las soluciones, todas pueden ser obtenidas a partir del cuadrado mágico “buduh” a través de simetrías y rotaciones. Por ejemplo, la primera que se muestra es el cuadrado “buduh” con una simetría respecto a la fila del medio y la última se obtiene mediante un giro de 180º. Por lo tanto, existe únicamente una solución “básica”, es decir, salvo simetrías y rotaciones.
Si se consideran cuadrados mágicos de orden 4, es decir, cuadrados 4×4 en los que se introducen los números del 1 al 16, la cosa cambia, puesto que hay 880 distribuciones básicas posibles (de nuevo salvo rotaciones y simetrías), como demostró el matemático aficionado francés Bernard Frenicle de Bessy (1605-1675), que se extienden hasta 7.040 si consideramos además los que se obtienen de los anteriores mediante simetrías y giros. La constante de un cuadrado mágico de orden 4 es 34.
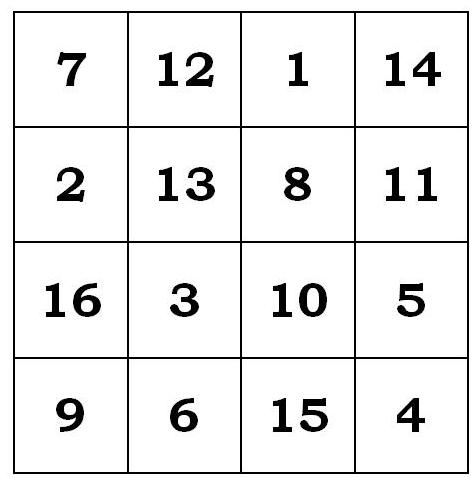
La primera representación gráfica de la que se tiene constancia en la que aparece un cuadrado mágico de orden 4 es una inscripción en un pilar de un templo de Khajurado (India).
Este es un cuadrado mágico especial. Su constante es 34; es decir,34 es lo que suma cada fila, columna y diagonal, aunque en este caso también es lo que suman las diagonales desplazadas, que son aquellas que aparecen si continuamos la última fila de la derecha con la primera de la izquierda, luego la segunda y la tercera, como se muestra en la imagen.
Pero aún hay más, también suman 34 otros grupos de cuatro elementos, casi los mismos que un cuadrado supermágico (véase más adelante).
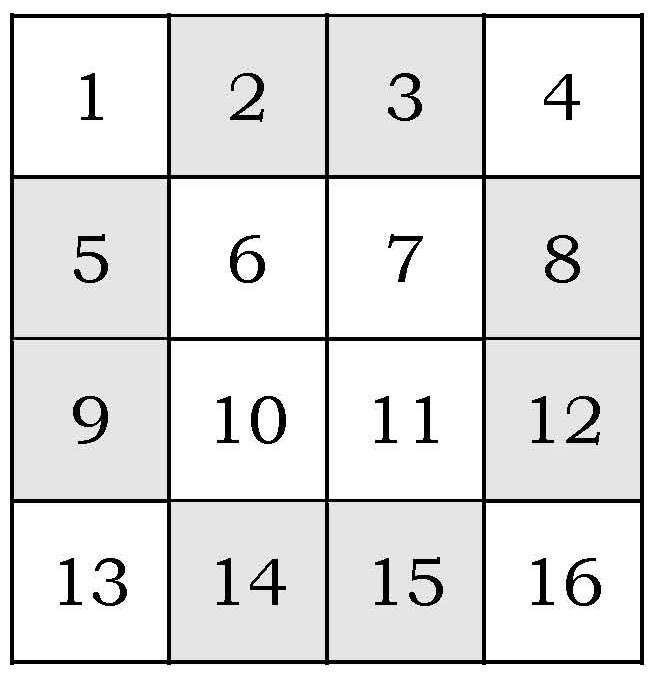
Existen diferentes métodos para generar cuadrados mágicos. Un método para generar cuadrados mágicos de grado múltiplo de 4 es mediante giros de 180º. Veámoslo para el cuadrado mágico de grado 4. En primer lugar se considera el cuadrado 4×4 en el que se han colocado los números del 1 al 16 en orden creciente (como se muestra en la imagen), y entonces se gira el cuadrado 180º, pero moviendo únicamente los números que están en el centro de los lados (los que están en casillas oscuras en el dibujo) y se obtiene así un cuadrado mágico 4×4.
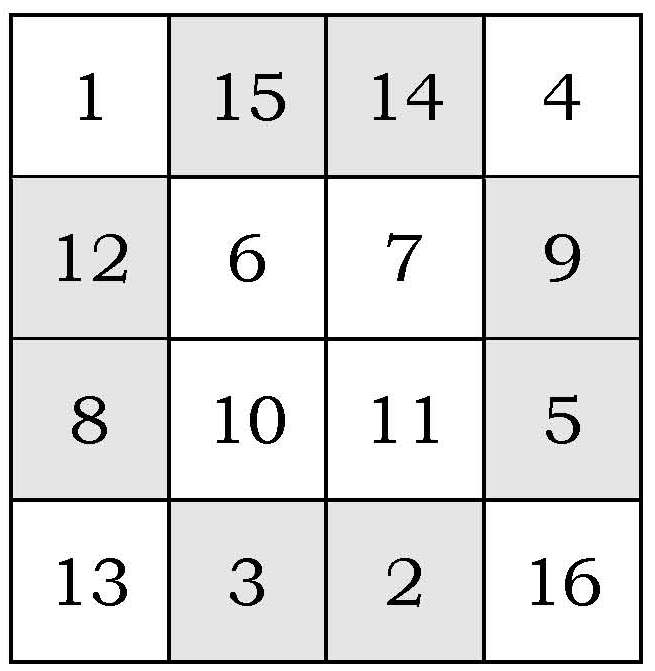
Si se invierte el orden de las filas (por ejemplo, la fila 1, 12, 8 y 13, pasa a ser 13, 8, 12, 1) y se cambia la primera fila por la cuarta, tal y como se muestra aquí…
…se obtiene el cuadrado mágico que aparece en el cuadro Melancolía (1514) de Durero.
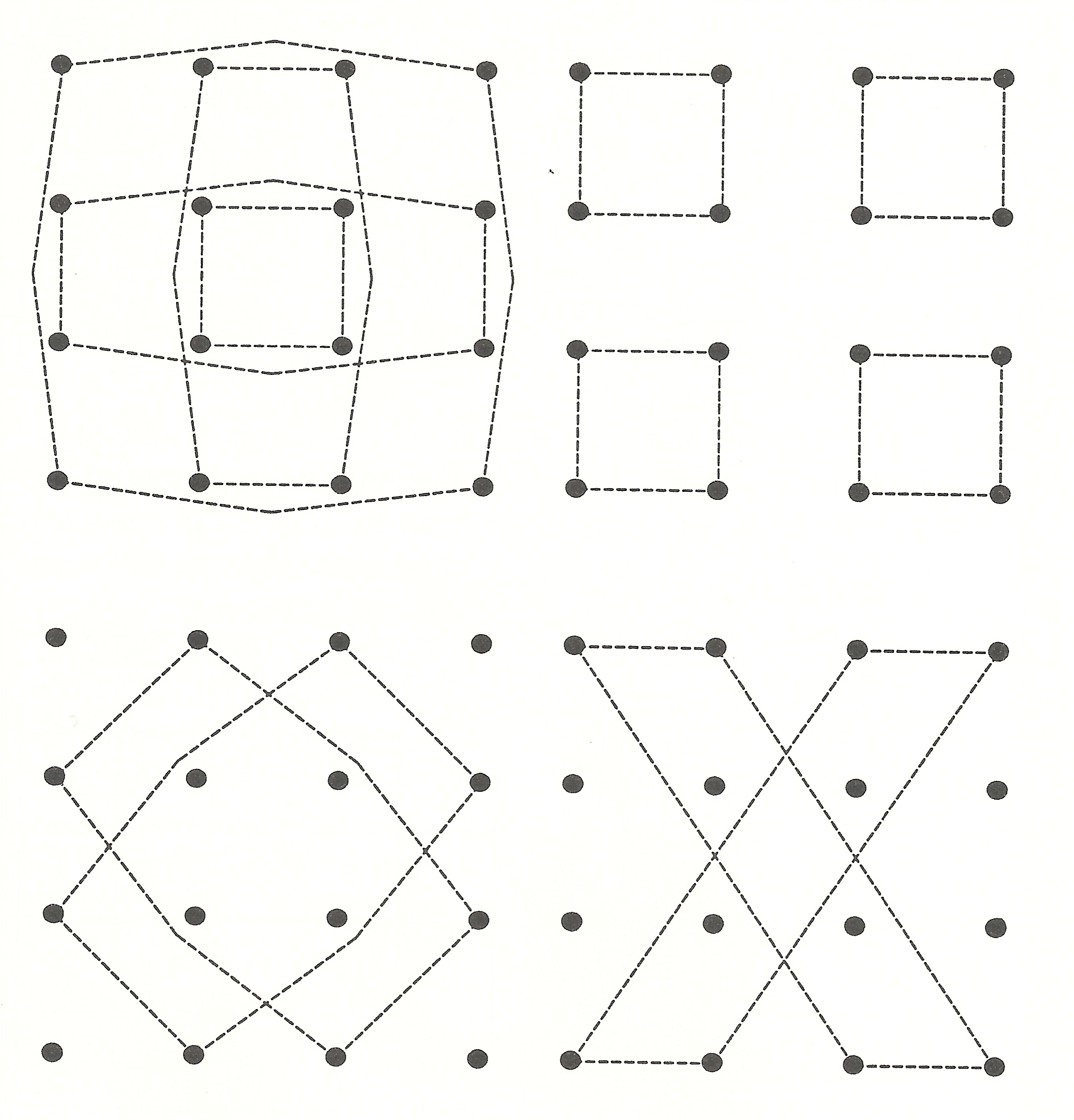
Este es un cuadrado muy particular. Durero pintó este cuadro en 1514, lo cual quedó reflejado en el cuadro a través del cuadrado mágico, puesto que los números del centro del lado inferior son precisamente 15 y 14. Además, es un cuadrado supermágico, la constante 34 se obtiene de 22 formas distintas, la suma de los elementos de las cuatro filas, las cuatro columnas y las dos diagonales, que son las 10 habituales, más las 12 reflejadas en los diagramas siguientes, que son las sumas de los cuatro números que están en las esquinas de los cuadriláteros representados.
Pero para el cuadrado supermágico de Durero también suman 34 las cuatro esquinas de los siguientes dos cuadriláteros.
Aunque las curiosidades de este cuadrado supermágico no terminan aquí, puesto que además se verifica que: i) la suma de los cuadrados de los números de las dos primeras filas (resp. columnas) es igual a la suma de los cuadrados de los números de las dos últimas filas (resp. columnas); ii) la suma de los cuadrados de los números de las filas (resp. columnas) primera y tercera es igual a la suma de los cuadrados de los números de las filas (resp. columnas) segunda y cuarta; iii) la suma de los números de las diagonales es igual a la suma de los números que no están en las diagonales; iv) la suma de los cuadrados de los números de las diagonales es igual a la suma de los cuadrados de los números que no están en las diagonales; v) la suma de los cubos de los números de las diagonales es igual a la suma de los cubos de los números que no están en las diagonales.
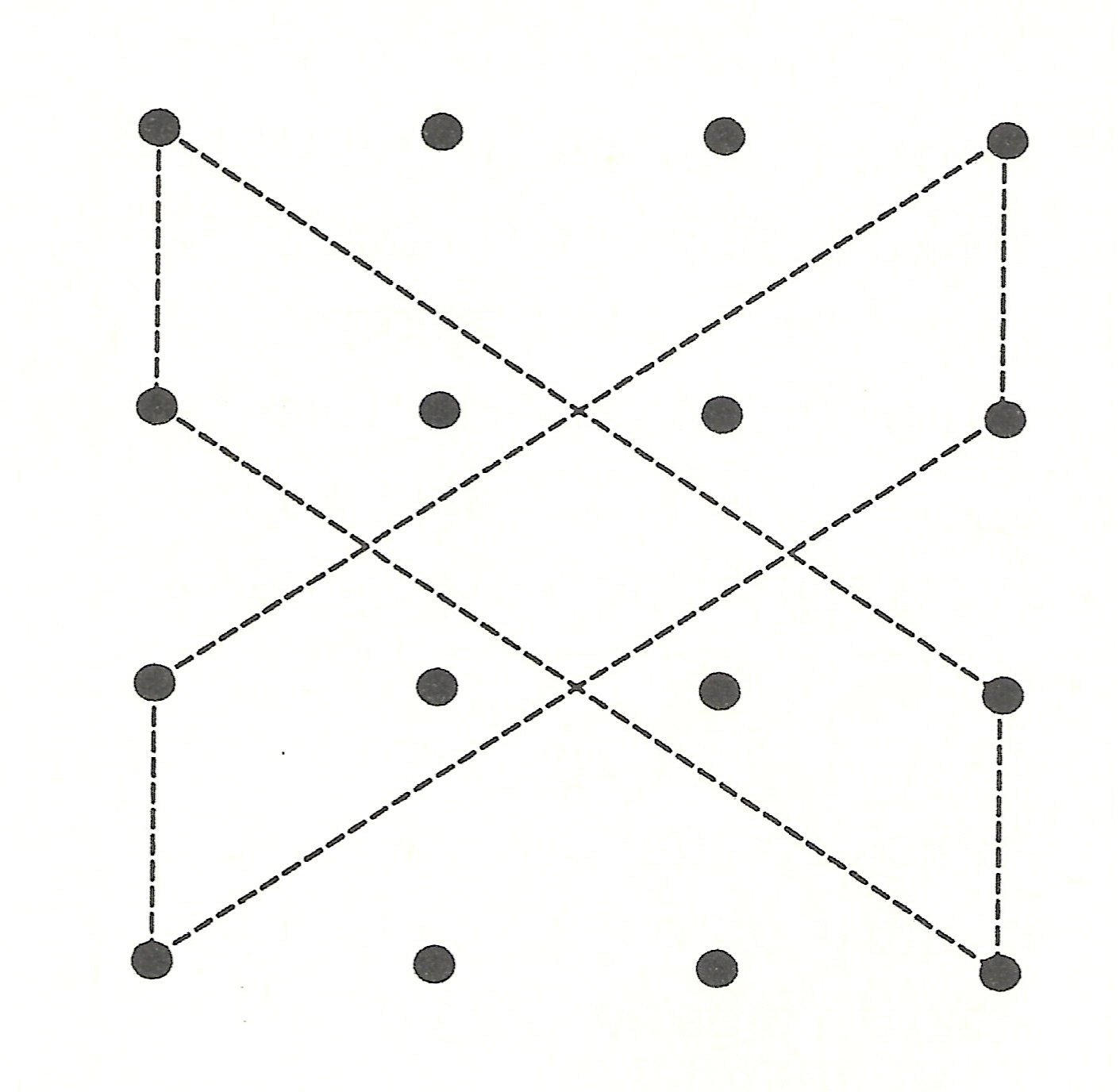
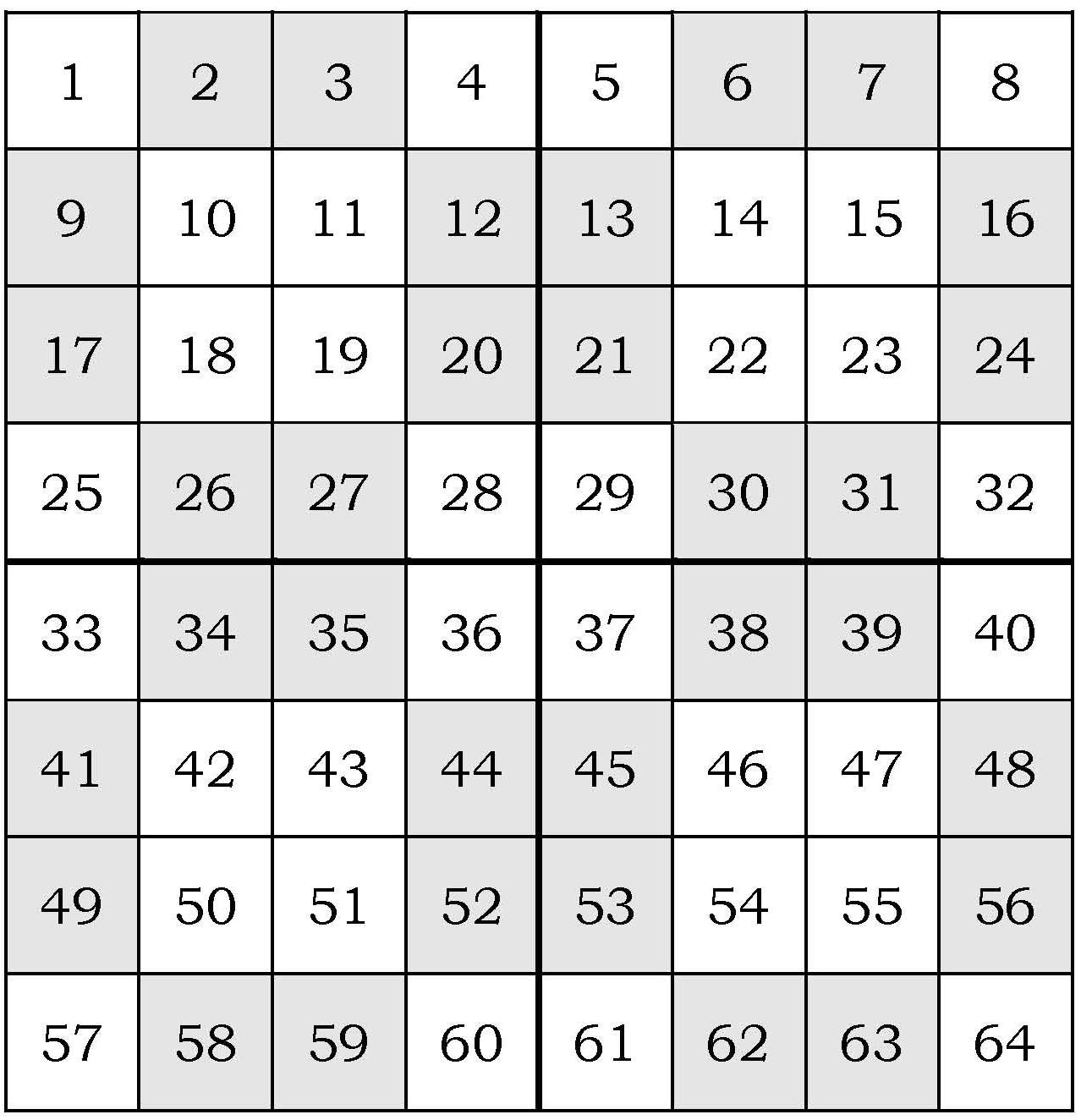
Pero volvamos al método para generar cuadrados mágicos de orden múltiplo de 4. Para el caso de orden 8 el método consiste en lo siguiente. Al igual que en el orden 4 se colocan los números del 1 al 64 de forma consecutiva en un cuadrado 8×8, como se muestra en la imagen.
Pero, ¿qué números se mueven al realizar el giro de 180º en esta construcción? Aquellos que están en el centro de los lados de los cuatro cuadrados 4×4 en los que podemos dividir el cuadrado 8×8 (los que son oscuros en el dibujo). Dejamos al lector, o lectora, de este artículo el placer de construir el cuadrado mágico 8×8 que resultará, y que es el cuadrado mágico que antiguamente se relacionó con Mercurio. La constante de los cuadrados mágicos de orden 8 es 120.
En la literatura pueden verse otros métodos para construir cuadrados mágicos de órdenes 4k (4, 8,…) como los anteriores, y también de órdenes 4k+2 (6, 10,…).
De igual forma, existen métodos para generar cuadrados mágicos de orden impar. Veremos dos ejemplos ilustrativos para orden 5. El primer método es el conocido como método de Loubère, en referencia a Simon de la Loubère, quien aprendió este método cuando estuvo de embajador de Louis XIV en Siam, la actual Tailandia, en 1687-88 (método siamés). Consiste en coger un cuadrado 5×5 y colocar el número 1 en el centro de la fila superior e ir colocando los siguientes números (2, 3, 4,…) en un recorrido diagonal ascendente y hacia la derecha, de forma que cuando se llega a la fila superior del cuadrado se continua por la inferior y cuando se llega a la columna derecha se continua por la de la izquierda, y con una condición más para cuando no es posible seguir ese recorrido, entonces se coloca el siguiente número en la casilla que está debajo del último número situado en el cuadrado, y se continua con el recorrido diagonal ascendente hacia la derecha (aquí podemos observar la descripción que realizó Loubère del método siamés de crear cuadrados mágicos, en su publicación de 1693, Una nueva relación histórica del reino de Siam).
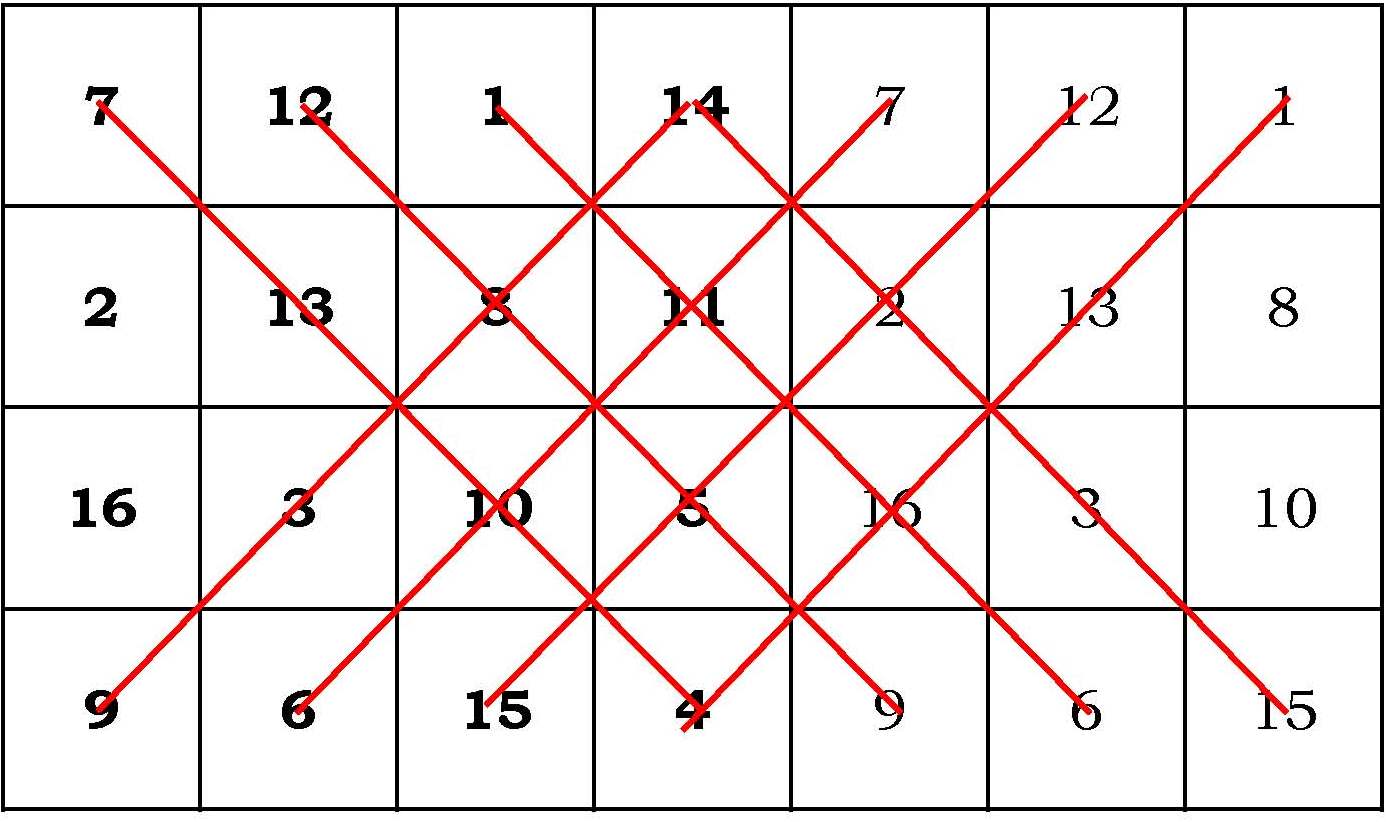
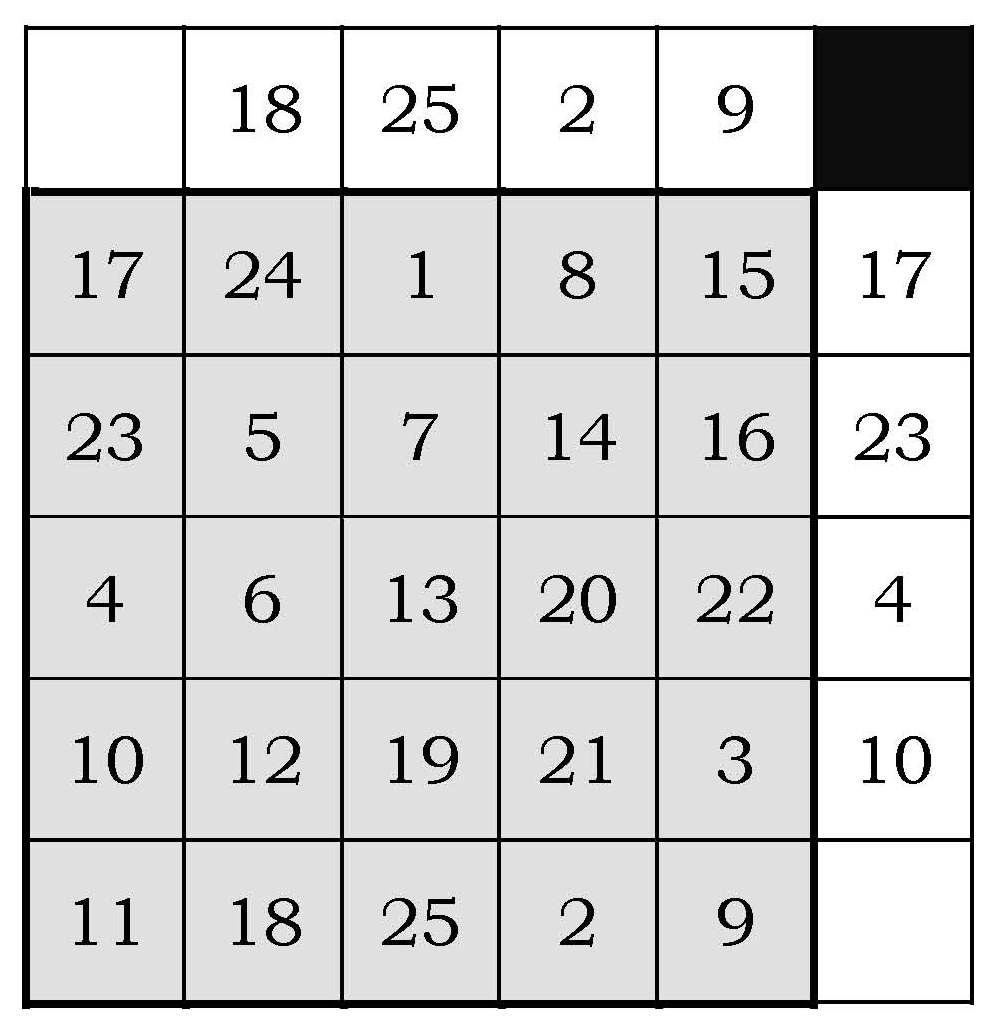
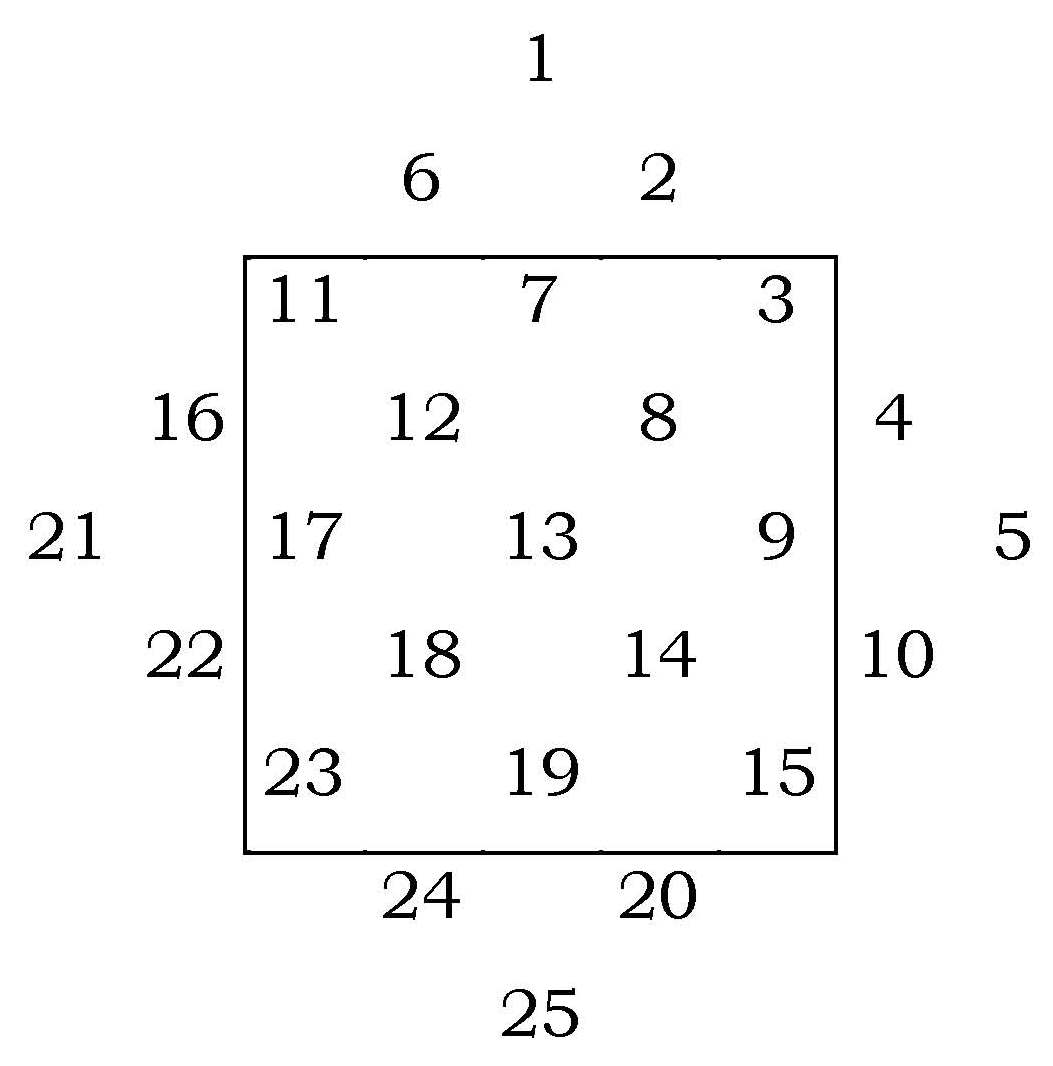
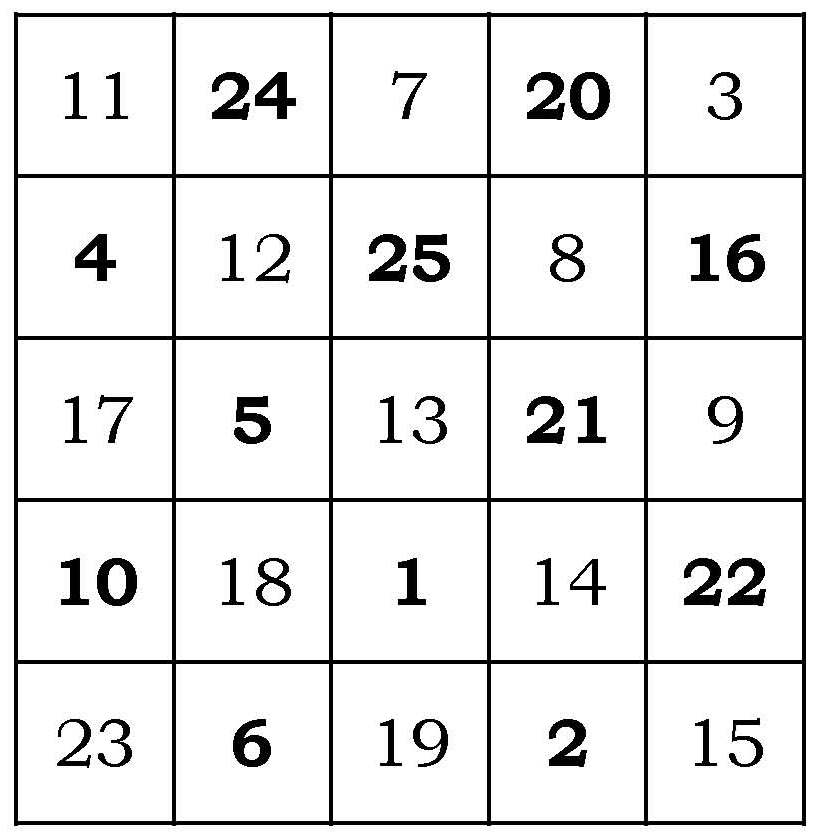
Este es el método que empieza a utilizar Dodola en la novela gráfica cuando quiere construir un cuadrado mágico 7×7 para distraer al Sultán. El segundo método consiste en distribuir los números del 1 al 25 en forma de rombo, como se muestra en la imagen. Se traza una cuadrícula 5×5 centrada en el 13 (que es el número que estará en el centro) y se sitúan dentro de la cuadrícula aquellos números que han quedado fuera, pero colocándolos en la parte contraria, obteniéndose así el deseado cuadrado mágico.
Se sabe que existen 275.305.224 cuadrados mágicos “básicos” de orden 5 (que fueron calculados por R. Schroeppel in 1973), pero se desconoce el número exacto de cuadrados mágicos de orden superior a 5. En orden 6 existe solo una estimación aproximada.
El concepto de cuadrado mágico se extendió más allá de los primeros números consecutivos a un conjunto cualquiera de números, a números primos, a números de Fibonacci, a números iguales, etc., pero de eso hablaremos otro día.
Nota: Esta anotación ha sido realizada por Raúl Ibáñez, profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica




cassandra araceli
todos los cuadros bienen del numero 15
Cuadrados latinos, matemáticas y arte abstracto – Cuaderno de Cultura Científica
[…] 2.- Habibi y los cuadrados mágicos II […]
666, el número de la Bestia (1) – Cuaderno de Cultura Científica
[…] Cultura Científica dedicadas a los cuadrados mágicos son Habibi y los cuadrados mágicos (parte 1; parte 2 y parte […]
La amante cartesiana, una historia matemática | Economía Personal
[…] 2011), de Craig Thompson (véase Habibi y los cuadrados mágicos, parte 1, parte 2 y parte 3), y otra a las matemáticas del cómic Ken Games (Diábolo, 2009-10), […]
Guía matemática para el cómic ‘Promethea’ — Cuaderno de Cultura Científica
[…] Como comentábamos en la tercera parte de la entrada del Cuaderno de Cultura Científica dedicada a la novela gráfica Habibi, los alquimistas europeos relacionaban Mercurio (y el metal del mismo nombre), con el siguiente cuadrado mágico de orden 8 (cuya constante es 260). Este es muy fácil de obtener como se explica en Habibi y los cuadrados mágicos II. […]
Carlos
https://scontent-mad1-1.xx.fbcdn.net/v/t1.0-9/122447532_2013518848788568_5285119708532656051_o.jpg?_nc_cat=101&ccb=2&_nc_sid=8bfeb9&_nc_ohc=aMWjBADamgIAX-528xe&_nc_oc=AQmcIi9l_GPcnAh-yXAZ7MZ0GDWWRh_b7yWXRoKubR5MMjYAml5zs30iyKqQt_pD19Q&_nc_ht=scontent-mad1-1.xx&oh=8d36480db2e022b1bc2b695066cffdfd&oe=5FB86831
TODAS LAS CASILLAS SUMAN 30, (CUADRADO MÁGICO, SAM LOYD CON UN SLIDING BLOCK PUZZLE)
Construyendo cuadrados mágicos — Cuaderno de Cultura Científica
[…] con los cuadrados mágicos de orden impar. En la entrada Habibi y los cuadrados mágicos II ya construimos todos los cuadrados mágicos de orden 3, que son solamente ocho, pero que, salvo […]