El sudoku es sin lugar a dudas uno de los rompecabezas más populares de los últimos tiempos, que ha tenido además un desarrollo vertiginoso. Todo el mundo lo relaciona con las matemáticas porque hay que colocar números en sus casillas, aunque su relación con esta ciencia es más profunda.
Desde que se diera a conocer internacionalmente el verano de 2005, el sudoku se ha convertido en todo un fenómeno de masas. Tenemos sudokus en los periódicos, revistas de sudokus, libros de sudokus, sudokus en todos los dispositivos electrónicos existentes (móviles, tabletas, ordenadores, etc), juegos de sudokus en las tiendas de juguetes, programas de ordenador para crear sudokus, colecciones por entregas relacionadas con el sudoku en los estancos, sudokus infantiles y una enorme cantidad de variantes del original.

Aunque seguramente las personas que estén leyendo esta entrada del Cuaderno de Cultura Científica ya conocerán perfectamente qué es un sudoku, empezaremos recordando las reglas de este pasatiempo matemático. El sudoku normal consiste en una cuadrícula de 9 x 9 celdas, dividida en 9 regiones de 3 x 3 celdas, y hay que rellenar las 81 celdas con las cifras del 1 al 9 (partiendo de una situación inicial en la que algunos números ya están colocados en algunas de las celdas), de manera que no se puede repetir ninguna cifra en una misma fila, columna o región. El sudoku está relacionado con los cuadrados latinos (véase la entrada Cuadrados latinos, matemáticas y arte abstracto o el libro Del ajedrez a los grafos, la seriedad matemática de los juegos) estudiados por el matemático Leonard Euler (1707-1783), aunque el juego moderno fue creado en la década de 1970 por el arquitecto jubilado y diseñador de pasatiempos Howard Garns (1905-1989) y publicado bajo en nombre number place en la revista Dell Pencil Puzzles & Word Games.
Maki Kaji, presidente de la editorial Nikoli, especializada en juegos y pasatiempos, en particular, rompecabezas lógicos, lo exportó a Japón y empezó a publicarlo en 1984 en su revista Monthly Nikolist bajo el nombre Suji wa dokushin ni kagiru (los números deben estar solos), que se abrevió a Su Doku. Su expansión por el resto del mundo vino de la mano del juez retirado neozelandés, residente en Hong Kong, Wayne Gould, quien desarrolló un programa de ordenador para crear rápidamente sudokus. En 2004 empezaron a publicarse sudokus en periódicos británicos, como The Times y The Guardian, y acabó convirtiéndose, desde 2005, en un rompecabezas muy popular que aparecía en la mayoría de los periódicos del mundo.
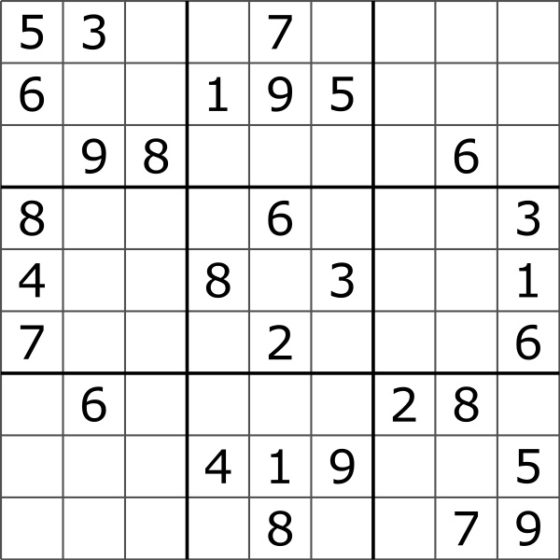

La relación del sudoku con las matemáticas no es que se utilicen números, ya que se podrían utilizar letras, colores o cualesquiera otros símbolos, sino que es de tipo combinatorio, está basada en la relación entre las diferentes posiciones de los símbolos (números) en las filas, columnas y regiones. Si observamos la solución de un sudoku, como la anterior imagen, se trata de un tipo particular de cuadrado latino (recordemos que un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n, de tal forma que cada número de {1, …, n} aparece una vez, y sólo una vez, en cada fila y cada columna) de tamaño 9 x 9, en el que se verifica también que los números del 1 al 9 aparecen solo una vez en cada una de las nueve regiones 3 x 3.

Existen diferentes cuestiones matemáticas implicadas en este rompecabezas, como cuántas estructuras de solución, es decir, cuadrados latinos de orden 9 que cumplen la regla de las regiones diferentes, hay (que resultan ser 6.670.903.752.021.072.936.960, aunque si tenemos en cuenta las simetrías, estas se reducen a 5.472.730.538 soluciones de sudokus distintas); dado un cuadrado latino de orden 9 que es solución de sudoku, cuántos rompecabezas sudokus distintos se pueden generar a partir del mismo (es decir, eliminando los números de las casillas hasta dejar una pequeña cantidad inicial que es el punto inicial del juego, las pistas) y cuál es la cantidad mínima de números iniciales (pistas) que se necesitan para que el sudoku esté bien definido, esto es, que exista una solución única (que resultan ser 17 pistas), entre otras.
Sin embargo, mi intención en esta entrada de la sección Matemoción del Cuaderno de Cultura Científica no es hablar de las matemáticas de los sudokus (puede verse, por ejemplo, el artículo Sudokus y modelización, de María Merino), sino presentar otros rompecabezas matemáticos similares a este, en el sentido de que se colocan números sobre una estructura reticular.
En el año 2010, Jai Gomer, de Kobayaashi Studios, desarrolló una serie de rompecabezas numéricos, llamados sujiko y suko, herederos de los sudokus, pero que ya implican algo de aritmética –en concreto la suma– en sus reglas. Estos aparecieron primero en los periódicos ingleses como The Times y The Telegraph, y posteriormente en periódicos de todo el mundo, como, por ejemplo, El País.
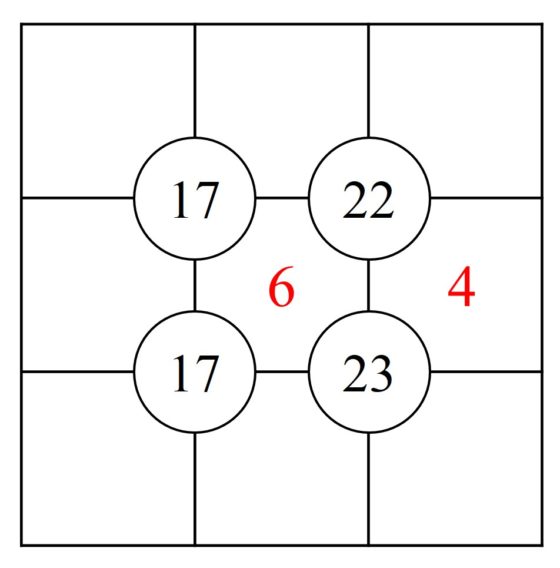
El tablero del sujiko es una cuadrícula 3 x 3, con cuatro espacios circulares colocados en las cuatro intersecciones de las líneas horizontales y verticales de la cuadrícula, en los cuales hay escritos cuatros números (por ejemplo, 17, 22, 17, 23, en la imagen anterior). El objetivo del pasatiempo es colocar los números del 1 al 9 en las celdas –aunque puede haber ya alguno colocado, como pista (en el sujiko anterior 6 y 4)– de forma que la suma de los números que estén en los recuadros alrededor de cada círculo es exactamente el número escrito en el mismo.
Este rompecabezas de resuelve de forma lógica, como el sudoku, pero teniendo en cuenta su regla, que la suma de los números de las celdas alrededor de un círculo es el valor del mismo. Veamos cómo resolver el sujiko anterior, que es de los sencillos.
Los números de las dos casillas de arriba a la derecha deberán sumar 12, ya que 6 y 4 están también alrededor del 22 y su suma es 6 + 4 = 10. Como en esas casillas no pueden estar 6 y 4, que ya están colocados, las dos opciones son 9 y 3, o 7 y 5, sin determinar aún cual va en cada una de las dos casillas. Si realizamos el mismo razonamiento para las dos celdas de abajo a la derecha, que deberán sumar 13, la única posibilidad es 8 y 5. Como aquí estaría el número 5, en las dos celdas de arriba tendrían que ser los números 9 y 3.
Veamos el orden arriba. En la casilla central de la fila de arriba va el 3 o el 9, si fuese el 9 tendríamos que alrededor de la casilla del 17 ya se sumaría 9 + 6 = 15, luego las otras dos casillas deberían sumar 2, lo cual es imposible, puesto que la suma más baja posible sería 1 + 2 = 3. En conclusión, en la primera fila, el número 3 iría en la casilla central y el 9 en la derecha.
Antes de seguir, pensemos en que tres números nos faltan de utilizar para las celdas de la columna de la izquierda. Serían 1, 2 y 7. Entonces, alrededor del 17 de arriba tenemos 3 + 6 = 9, más la suma de los números de las dos celdas, que deberá ser 8, luego los números de esas dos celdas son 1 y 7. Si seguimos este razonamiento un poco más, obtendremos la solución definitiva, que aparece en la imagen de abajo.
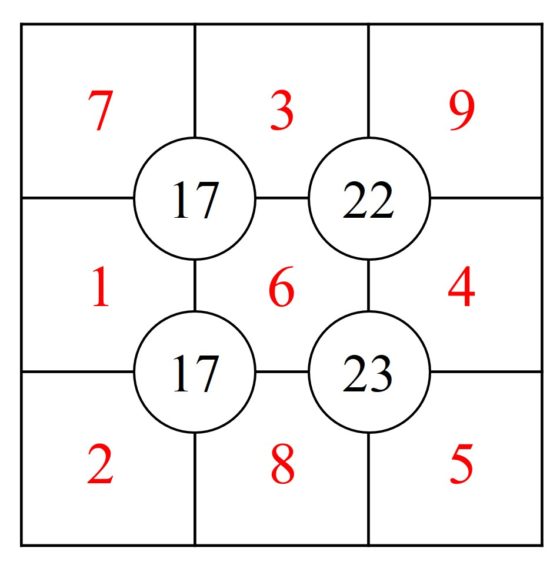
Podemos presentar este problema de la siguiente forma. La información del mismo está dada en el siguiente esquema, donde en las celdas tenemos las variables del juego y en los círculos los datos del mismo.
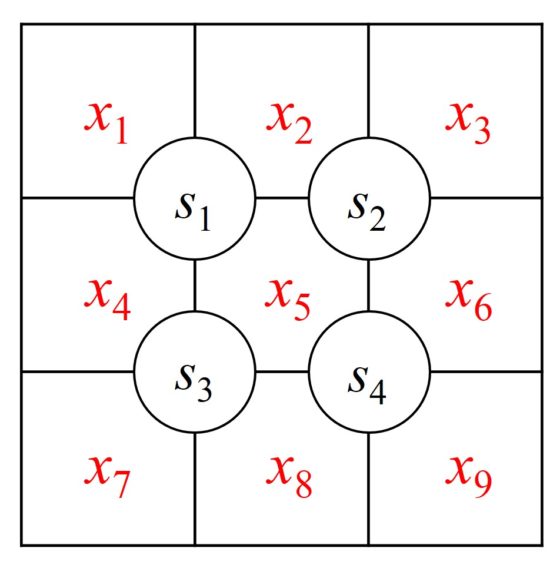
Luego la solución del sujiko es la solución de un sistema de cuatro ecuaciones y nueve incógnitas, aunque con las siguientes restricciones, las variables solo toman valores entre los números 1, 2, 3, 4, 5, 6, 7, 8, 9 y cada variable toma un valor distinto a las otras.
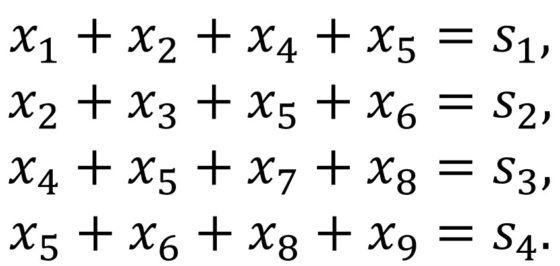
Aunque la diversión del sujiko está en obtener la solución de forma lógica, se puede utilizar también el planteamiento algebraico como ejemplo para estudiantes que estén trabajando el álgebra lineal de la resolución de los sistemas de ecuaciones lineales.
Os dejo con dos sujikos, de niveles medio y alto, que he sacado de la página Sudokasana, donde se denominan Minisum puzzles. Aunque también podéis encontrar sujikos en la página de pasatiempos del periódico The Times.
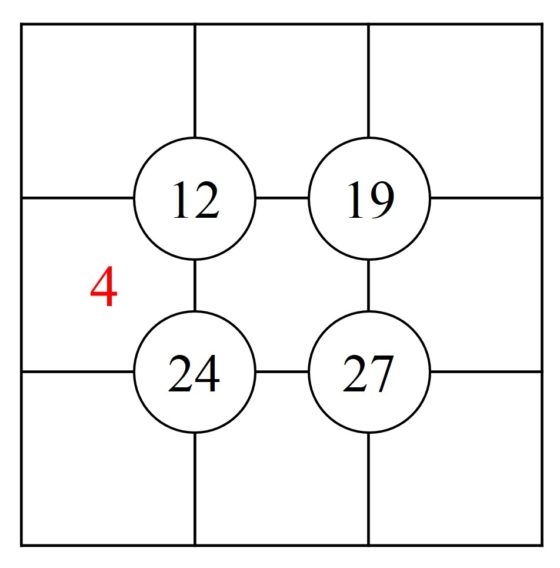
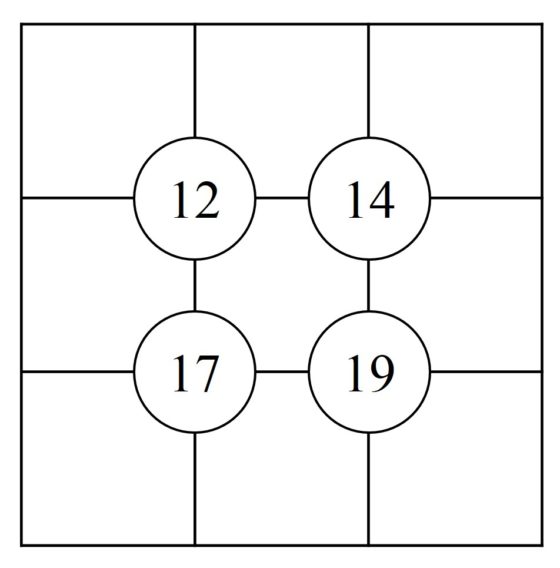
Por otra parte, el rompecabezas suko es como el sujiko, pero al que se le añade una nueva condición relacionada con regiones del retículo 3 x 3. La condición es que la suma de los números de las casillas de un mismo color suman la cantidad indicada en el pasatiempo, como aparece en la siguiente imagen (suko que hemos tomado de la página de pasatiempos de The Times).
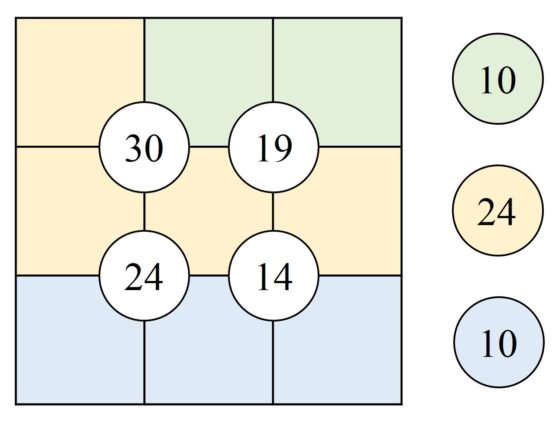
Desde el punto de vista algebraico, en el suko añadimos tres ecuaciones lineales más, luego tenemos un sistema de siete ecuaciones lineales con nueve incógnitas, y la solución del rompecabezas es la solución del sistema de ecuaciones.
Otro rompecabezas relacionado con el sudoku, o más bien con los cuadrados latinos, pero que añade aritmética –aunque ahora las cuatro operaciones aritméticas, no solo la suma– a sus reglas es el KenKen.
El rompecabezas KenKen, también conocido con los nombres KenDoku, MathDoku o CalcuDoku, fue inventado por el profesor de matemáticas japonés Tetsuya Miyamoto como una herramienta para ejercitar el cerebro. Su nombre se deriva del vocablo japonés Ken que significa inteligencia o ingenio.
En 2007 el inventor de juguetes Robert Fuhrer, propietario de la empresa de juguetes Nextoy, descubrió en Japón varios libros con este pasatiempo y su interés por el mismo haría que el rompecabezas lógico acabara en las páginas del periódico británico The Times y después en muchos otros periódicos de todo el mundo.
Las reglas del KenKen son las siguientes. Se parte de una cuadrícula n x n sobre la que hay que colocar los números de 1 a n de forma que en cada fila y cada columna estén todos los n números y no se repita ninguno (luego será un cuadrado latino de orden n), pero además la retícula está dividida en una serie de regiones, en cada una de las cuales aparecen una operación aritmética (suma, resta, multiplicación o división) y un número, que será el resultado de aplicar la operación aritmética indicada a los números de las celdas de esa región.
En el siguiente ejemplo de rompecabezas KenKen tenemos una cuadrícula 4 x 4, luego hay que escribir los números 1, 2, 3 y 4 en las celdas de la misma, de forma que se constituya un cuadrado latino –en cada fila y cada columna aparece cada uno de los cuatro números una y solo una vez– y se cumplan las condiciones aritméticas de las regiones –por ejemplo, en la región de arriba a la izquierda la división de los dos números es 2, o en la región de la derecha la resta de los dos números es también 2–.
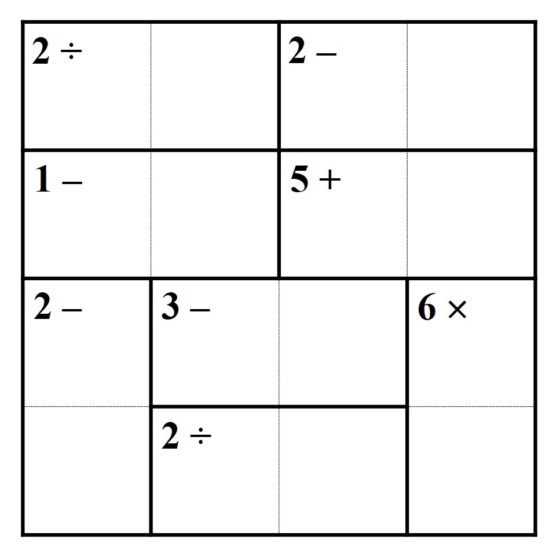
La solución de este KenKen viene dada en la siguiente imagen.
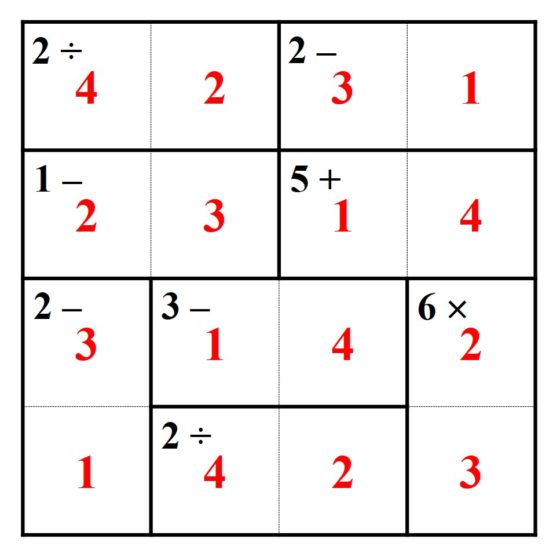
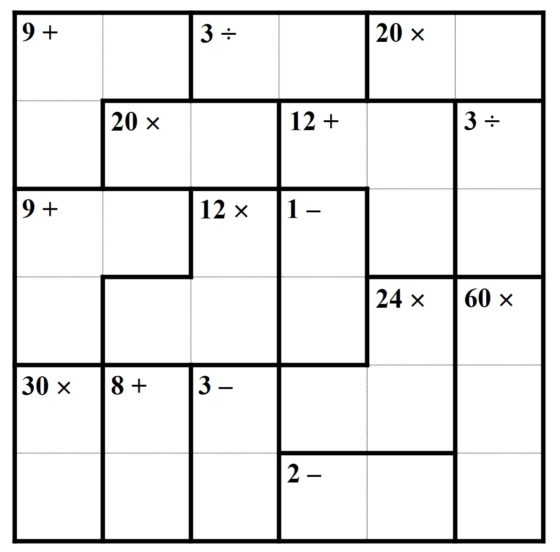
En la página KenKen, puzzles that make you smarter se pueden encontrar rompecabezas con cuadrículas desde 3 x 3 hasta 9 x 9, de diferentes niveles de dificultad. Os dejamos con uno para que os divirtáis de tamaño 6 x 6 y dificultad media.
Otro de los juegos de la editorial Nikoli, famosa internacionalmente por el Sudoku, es el Hitori, término que en japonés significa “solitario”. Este pasatiempo consiste en una retícula con números en todas sus celdas y la acción del mismo consiste en eliminar una serie de números, o pintar de negro las celdas correspondientes, de forma que se cumplan las siguientes reglas:
i) en cada fila y cada columna no se repite ningún número;
ii) las celdas tachadas o negras no pueden ser adyacentes (pueden tocarse esquina con esquina, pero no lado con lado);
iii) el resto de las celdas con números tienen que estar conectadas, vertical u horizontalmente, entre sí, es decir, no pueden quedar celdas aisladas.
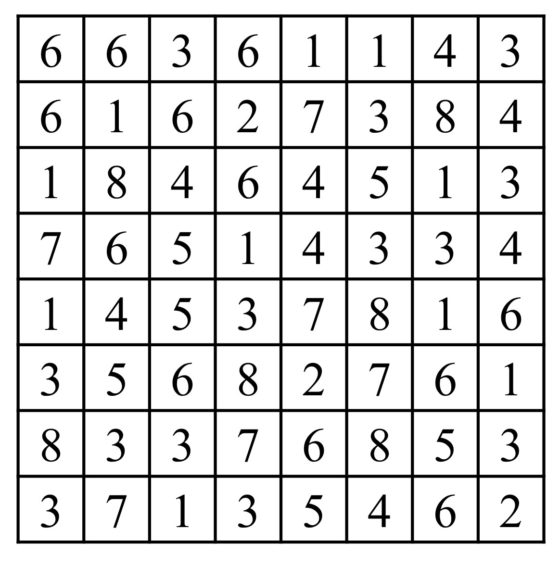
Veamos en qué consiste el juego mediante un ejemplo concreto de tamaño 5 x 5.
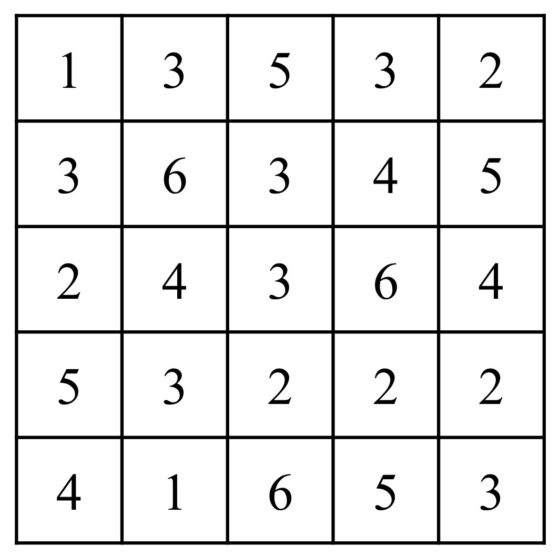
La solución aparece en la siguiente imagen. Como podemos observar, se cumplen las tres condiciones de este rompecabezas lógico. En cada fila y cada columna de la solución no se repite ningún número, por ejemplo, en la primera fila había dos celdas con el número 3, luego se ha tenido que tachar una. Las celdas tachadas solo se tocan por los vértices o no se tocan. Y no hay celdas aisladas de las demás.

En la página Hitori Conquest [www.hitoriconquest.com/] pueden encontrarse más rompecabezas Hitori de tamaños 5 x 5, 8 x 8 y 12 x 12, como el que dejamos a continuación para aquellas personas que queráis pasar un buen rato resolviéndolo.
Vamos a concluir esta entrada del Cuaderno de Cultura Científica con otro de los rompecabezas lógicos popularizado por la editorial japonesa Nikoli, el conocido como Numberlink (que podríamos traducir como “conecta los números”). Este juego tiene su origen en la matemática recreativa clásica, ya que una versión del mismo fue propuesta por el matemático recreativo estadounidense Sam Loyd (1841-1911) en 1897 y también por el matemático recreativo inglés Henry Dudeney (1857-1930), en su libro Amusements in Mathematics (1917), el problema 252, que vemos en la siguiente imagen.

El rompecabezas consiste en una retícula en la que aparecen parejas de números (aunque también podrían ser letras, colores u otros símbolos), dos unos, dos doses, dos tres, etcétera. El jugador tiene que conectar cada número con su igual mediante una línea que pasa de una celda a otra, horizontal o verticalmente, de tal forma que las líneas no se pueden cruzar entre sí, ni volver hacia atrás a celdas ya recorridas y no debe de quedar ninguna celda sin ser recorrida por alguna línea (aunque hay algunos diseñadores de juegos que se saltan esta regla).
Veamos un sencillo ejemplo y su solución.
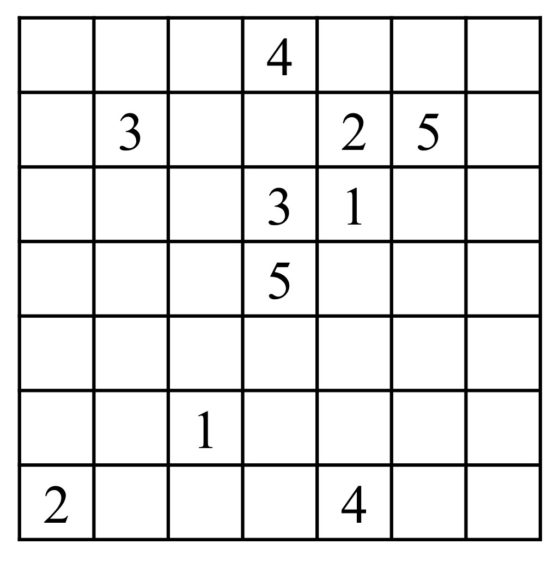
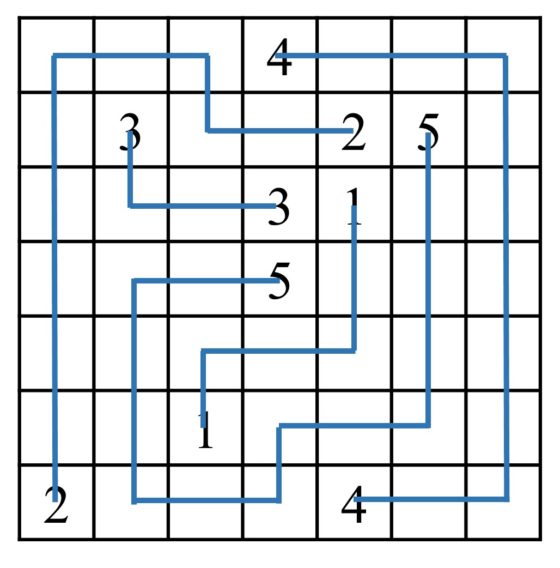
Os dejamos propuesto un rompecabezas lógico conecta los números, sacado de la página Puzzle’s Baron Numberlinks, para vuestro disfrute.
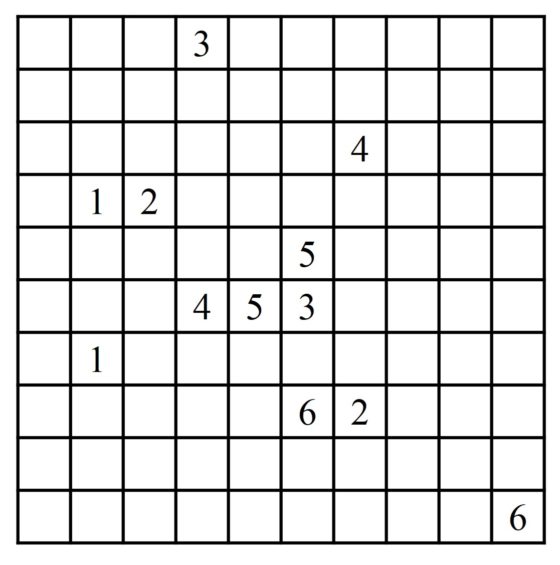
Para todos los rompecabezas lógicos presentados en esta entrada existen aplicaciones para móviles que os podéis bajar y jugar en cualquier momento. Yo mientras escribía esta entrada me he bajado algunas a mi móvil para poder jugar tranquilamente.

Bibliografía
1.- Raúl Ibáñez, Sudoku, Las matemáticas en la publicidad, DivulgaMAT, 2011.
2.- María Merino, Sudokus y modelización, Un paseo por la Geometría 2009/2010, UPV/EHU, 2010.
3.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, RBA, 2015.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Carlos Gaceo
TODAS LAS CASILLAS SUMAN 30
(CUADRADO MÁGICO, SAM LOYD CON UN SLIDING BLOCK PUZZLE)
30 30 30 30 30
⋰
3 8 4 15 30
13 6 10 1 30
14 5 9 2 30
X 11 7 12 30
\
30
Anónimo
Cuadrados Mágicos que suman 30 (demostrado), composición en un puzzle de Sam Loyd.
Una recopilación de rompecabezas matemáticos con números – Tec Ofertas España
[…] Cuaderno de Cultura Científica han publicado esta interesante recopilación de Rompecabezas matemáticos con números, derivados del Su Doku (1984) fashioned de la editorial […]
Una recopilación de rompecabezas matemáticos con números – Celulares, smartphones y tablets
[…] Cuaderno de Cultura Científica han publicado esta interesante recopilación de Rompecabezas matemáticos con números, derivados del Su Doku (1984) original de la editorial […]
RECOPILACIÓN ROMPECABEZAS MATEMÁTICOS | JALCA Blog
[…] de Cultura Científica han publicado esta interesante recopilación de Rompecabezas matemáticos con números, derivados del Su Doku (1984) original de la editorial […]
Más rompecabezas matemáticos con números — Cuaderno de Cultura Científica
[…] mi anterior entrada del Cuaderno de Cultura Científica Rompecabezas matemáticos con números presentamos una serie de pasatiempos matemáticos con números relacionados con el sudoku, algunos […]
Resumen de lecturas compartidas durante octubre de 2020 | Vestigium
[…] Rompecabezas matemáticos con números. ~ Raúl Ibáñez. #Matemáticas […]
Shikaku y otros puzles con números
[…] del sudoku. Los rompecabezas sujiko, suko, KenKen, hitori y numberlink se incluyeron en la entrada Rompecabezas matemáticos con números, mientras que la entrada Más rompecabezas matemáticos con números se dedicó a los rompecabezas […]