Cuando hace un año escribí la entrada ¿Pueden los números enamorarse de su propia imagen? decidí dejar para más adelante el hablar de los números conocidos como “errores de impresión”. Ahora, mientras reflexionaba frente a mi ordenador sobre cuál podría ser mi siguiente entrada para el Cuaderno de Cultura Científica, me he acordado de esta familia tan singular de números y me ha parecido que era un buen momento, en mitad de esta larga cuarentena por el coronavirus, para hablar de ellos.

El origen de este tipo de números está en un rompecabezas del gran matemático recreativo inglés Henry E. Dudeney (1857-1930), perteneciente al libro Amusements in Mathematics (1917), que dice lo siguiente.

Problema 115, El error de impresión: Para cierto artículo un impresor tenía que escribir 5⁴2³, es decir, la multiplicación de la potencia cuarta de 5 (625) por el cubo de 2 (8), cuyo resultado es 5000. Sin embargo, el impresor cometió un error y escribió la expresión 5423, en lugar de la deseada 5⁴ 2³, lo cual no era correcto. ¿Podrías buscar un número de cuatro dígitos para el cual el error del impresor no hubiese tenido importancia, es decir, las dos expresiones tendrían el mismo valor?

La solución, que es única, a este problema de ingenio es el número 2592, puesto que

Sin embargo, en el libro de Henry Dudeney no encontramos ninguna explicación, tan solo la respuesta al rompecabezas. Este problema fue propuesto de nuevo unos años más tarde, en 1933, por el matemático norteamericano Raphael M. Robinson (1911-1995), como problema E69, en la revista American Mathematical Monthly. La solución, con su correspondiente demostración (es un análisis de los posibles valores de a, b, c y d, en la expresión a^bc^d= abcd, eliminando todos menos la solución conocida), fue publicada un año después en la misma revista por el matemático Charles W. Trigg (1898-1989).

El aficionado a la matemática recreativa, Donald L. Vanderpool (1930-2010), de Towanda (Pensilvania), no solo se interesó por este problema, sino por encontrar otros ejemplos que también fuesen “errores de impresión”. Del mismo estilo al planteado por Henry Dudeney, aunque el segundo número no era una potencia sino un número natural, encontró los siguientes ejemplos que mostramos a continuación.

Si se les añaden ceros a los números 425 y 325, se obtiene toda una familia infinita de ejemplos, aunque podemos considerar que son esencialmente el mismo.

Donald Vanderpool también obtuvo ejemplos de “errores de impresión” de otro tipo, en concreto, relacionados con las llamadas fracciones mixtas. Primero recordemos qué son estas. Una fracción mixta es una fracción impropia, es decir, el numerador es mayor que el denominador (ambos positivos), luego su valor es mayor que 1, que se representa como un número entero y una fracción propia. Por ejemplo, 3/2 es una fracción impropia, que se representa como 3/2 = 1 1/2, queriendo indicar que es la suma de 1 y 1/2 (esto es, 3/2 = 1 + 1/2, pero en la representación de la fracción mixta se omite el +). Este tipo de representaciones, las fracciones mixtas, se suele utilizar con las medidas (peso, volumen, tiempo, etc), por ejemplo, en las recetas de cocina. Así podemos leer expresiones del tipo “1 1/2 cucharaditas de comino” o “1 3/4 kilogramos de carne picada de ternera” en cualquier libro de recetas de cocina que tengamos en casa, por mencionar alguno, el clásico 1080 recetas de cocina, de Simone Ortega.

Los ejemplos de fracciones mixtas errores de impresión que obtuvo Vanderpool fueron los siguientes.

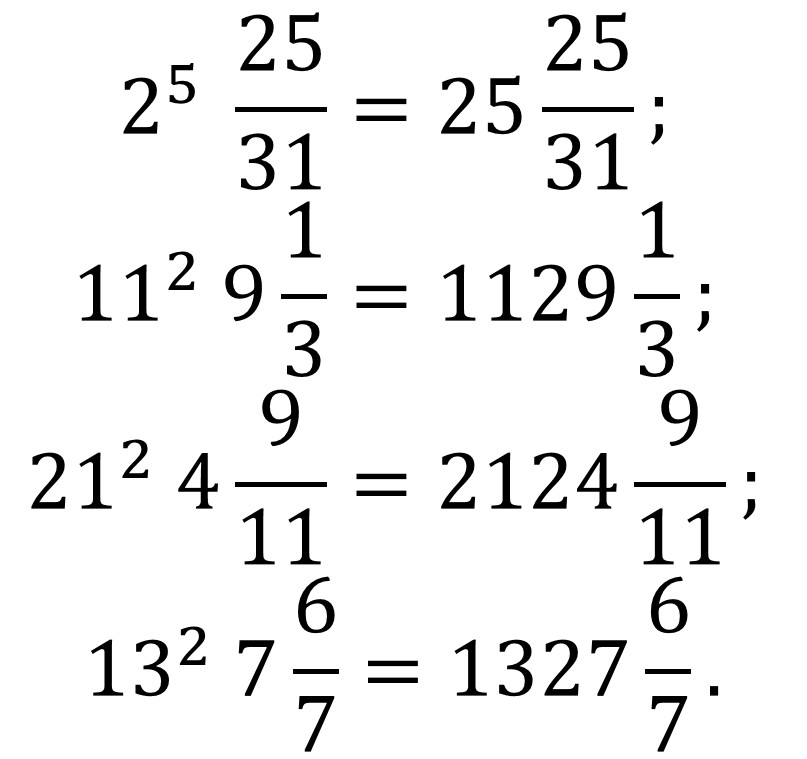
Estas fracciones son errores de impresión por lo siguiente.

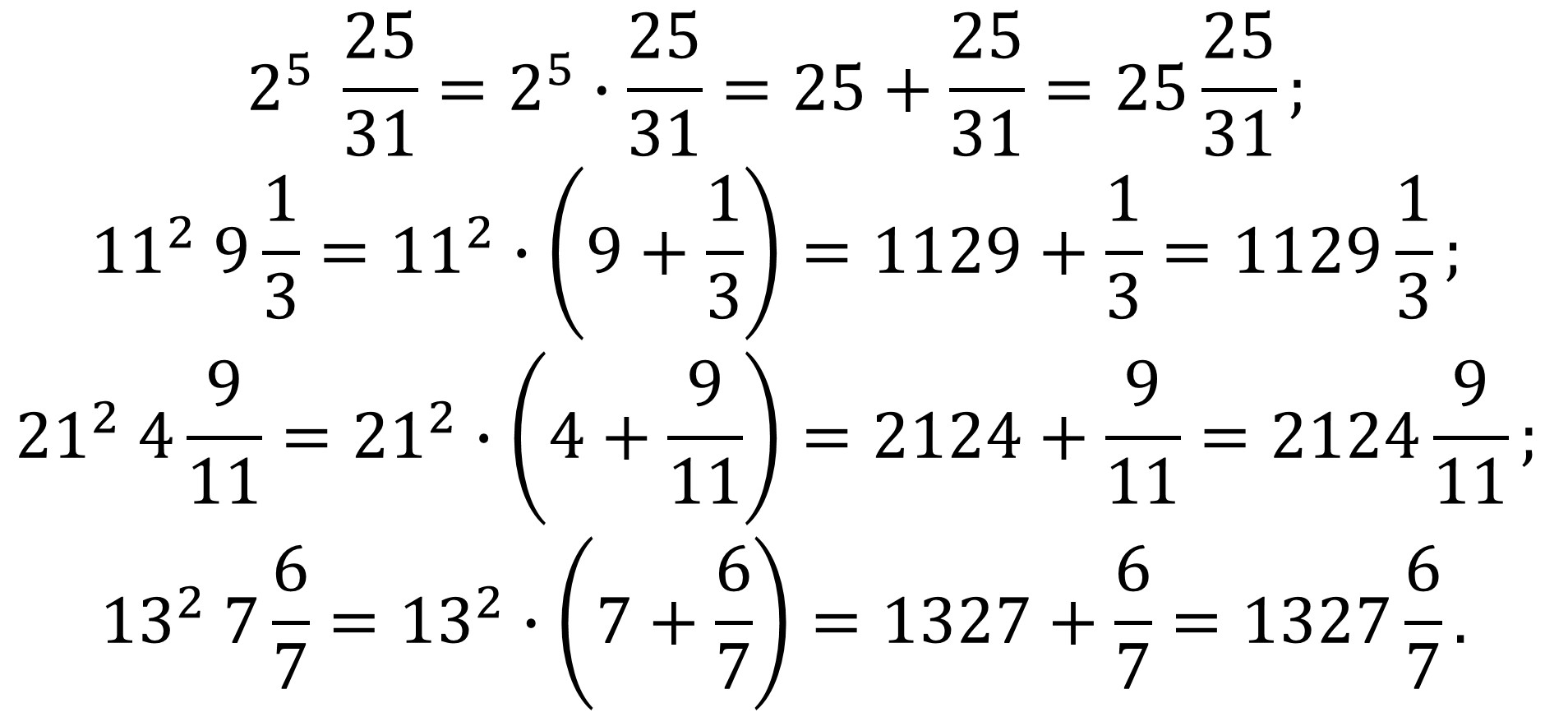
Pero volviendo a los números errores de impresión de tipo Dudeney, es decir, aquellos que son producto de diferentes potencias, es decir, de la forma n = a^b c^d e^f… = abcdef…, aunque tales que, como en los ejemplos de Vanderpool, pueden terminar en un número natural, estos se recogen en la Enciclopedia on-line de sucesiones de números enteros-OEIS como la sucesión A096298. Ahí podemos ver otros números errores de impresión de este tipo.

Si además estas expresiones también pueden empezar por el producto por un número, los llamados números errores de imprenta de segundo tipo (A116890 en la OEIS), tenemos más ejemplos. Algunos de ellos los mostramos aquí.

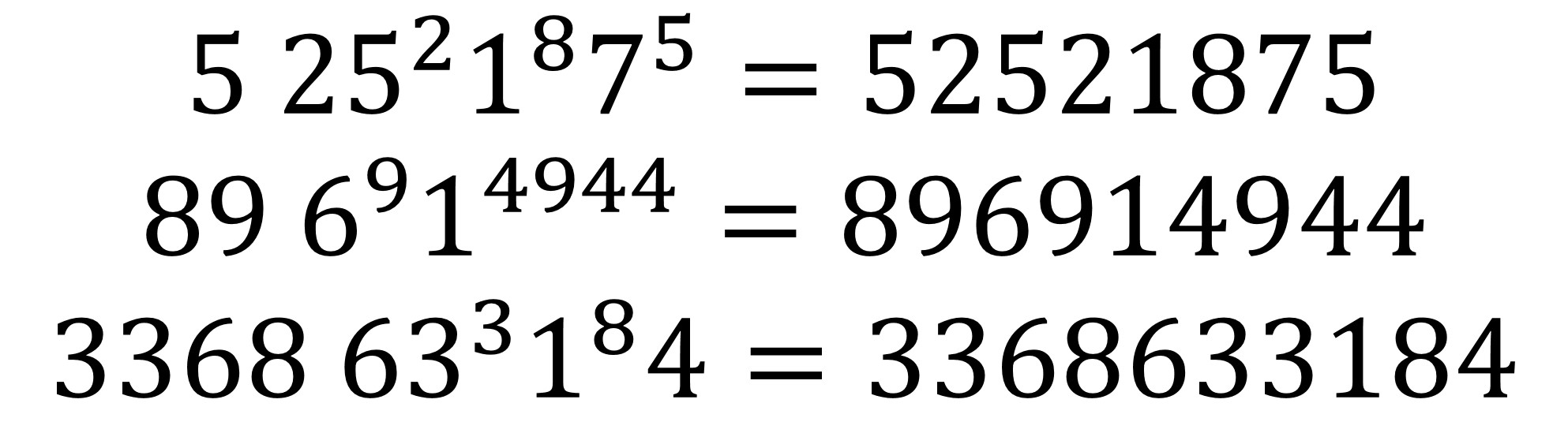
O si admitimos tanto potencias como multiplicaciones (espacios en blanco en la expresión matemática) tenemos más errores de imprenta (A156322 en la OEIS), como los siguientes.

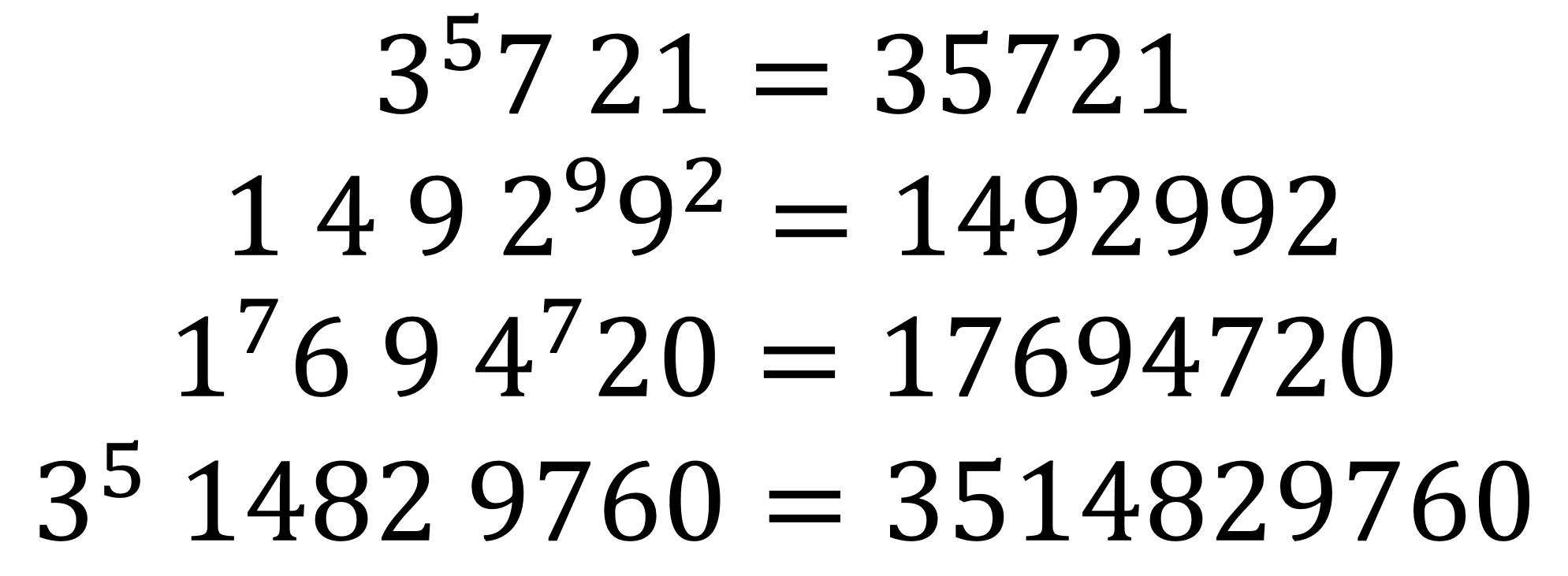
Observemos que el último ejemplo mostrado es pandigital, es decir, tiene las diez cifras básicas, del 0 al 9.

El químico y matemático recreativo estadounidense Joseph S. Madachy (1927-2014) cuando habla de los errores de impresión en su libro Mathematics on vacation, incluye el que caso en que pueda no haber potencias, solo espacios entre números que se entienden como multiplicaciones. El ejemplo que incluye Madachy para explicar esta posibilidad es el siguiente.

Pero volviendo al problema original, al rompecabezas de Henry E. Dudeney, podemos plantearnos si existirá un ejemplo de error de impresión que sea similar al de Dudeney en el siguiente sentido, que sea producto de potencias con un único dígito en la base y en el exponente, es decir, de la forma a^bc^de^f…y^z = abcdef…yz. El matemático británico-estadounidense Neil J. A. Sloane, creador de la Enciclopedia on-line de sucesiones de números enteros, demostró que existe sólo otro número como el de Dudeney, al menos para números menores que 10¹⁰⁰, teniendo en cuenta que matemáticamente 0⁰ = 1:

Y como en otras ocasiones vamos a concluir esta entrada del Cuaderno de Cultura Científica con una obra plástica relacionada con los números, en concreto, con el número error de impresión de Dudeney, el número 2592, aunque su autor no se haya inspirado en esta propiedad.

Bibliografía

1.- Henry Dudeney, Amusements in Mathematics, Thomas Nelson and sons,1917 (el original puede verse en la librería Internet Archive).

2.- Donald L. Vanderpool, Printer’s errors, Recreational Mathematics Magazine 10, p. 38, 1962.

3.- Joseph S. Madachy, Mathematics on vacation, Charles Scribner’s Sons, 1966.

4.- Wolfram MathWorld: Printers Errors

5.- Wolfram MathWorld: Mixed Fraction

6.- The On-line Encyclopedia of Integer Sequences

7.- Erich Friedman web page: Math Magic, Problem of the month (June 2001)

8.- Neil J. A. Sloane, Eight Hateful Sequences, Barrycades and Septoku: Papers in Honor of Martin Gardner and Tom Rodgers, American Mathematical Society, 2020.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica