No hace mucho tiempo escribí una entrada para esta sección del Cuaderno de Cultura Científica titulada Números errores de impresión en la cual estuvimos hablando de ciertos números que, aunque se produzca un cierto error tipográfico, siguen manteniendo su valor. Recordemos un ejemplo. Supongamos que queremos escribir en un artículo o una entrada de un blog el número “2 elevado a 5 multiplicado por 9 elevado a 2”, es decir, 25 92, pero se produce un error tipográfico y no quedan reflejadas las potencias, es decir, se queda escrito 2592. En general, esto produciría un error, ya que el valor de la expresión matemática no coincidiría con el valor del número, sin embargo, en este caso el resultado de 25 92 es, si realizamos las operaciones, 2592, luego sorprendentemente se mantiene inalterado. A estos números se les llama números errores de impresión.
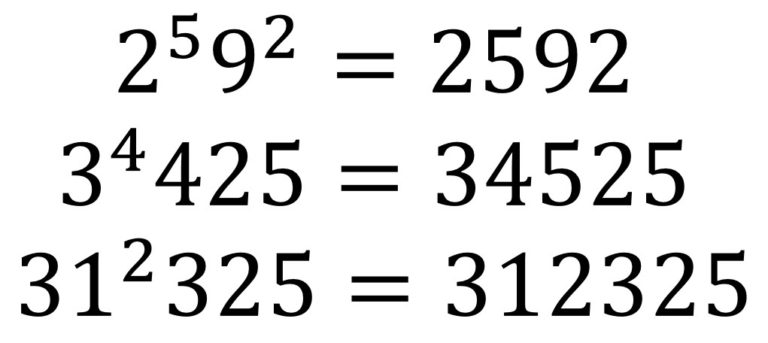
En esta entrada vamos a centrar nuestra atención en una serie de fracciones tales que, a pesar de producirse un error que podríamos calificar de matemático, en concreto, una cancelación anómala, el valor de la fracción se mantiene correcto. Veamos en qué consisten exactamente.
Empecemos con una sencilla fracción como es 12/15 (cuyo valor es 0,8). Como nos han enseñado cuando estudiábamos fracciones en la escuela, las fracciones como esta se pueden simplificar si tenemos en cuenta que 12 = 3 x 4 y 15 = 3 x 5, dividiendo el numerador y el denominador por un divisor común, en este caso, el 3. Es decir, “cancelamos” arriba y abajo el divisor común, luego 12/15 se transforma en 4 / 5 (cuyo valor sigue siendo 0,8).
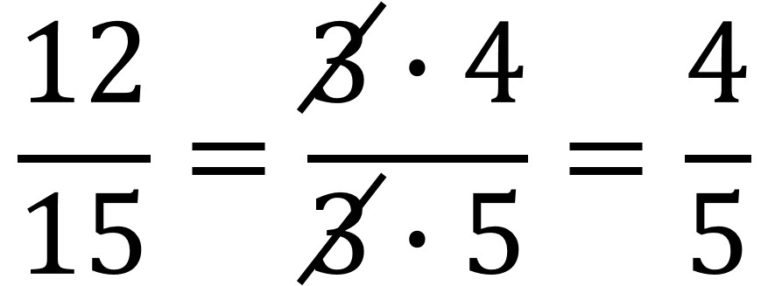
En las llamadas cancelaciones anómalas lo que ocurre es que se cancelan dígitos del numerador y del denominador como si fuesen divisores de los mismos. Esa cancelación que a priori daría lugar a un resultado completamente diferente, sin embargo, en el caso de las llamadas cancelaciones anómalas, lo que ocurre es que el resultado sorprendentemente no varía. Vamos a mostrar dos casos en los que se cancela un dígito del numerador y del denominador, viendo que en el primero el resultado es distinto, mientras que en el segundo el resultado es el mismo, obteniendo así un ejemplo de cancelación anómala.
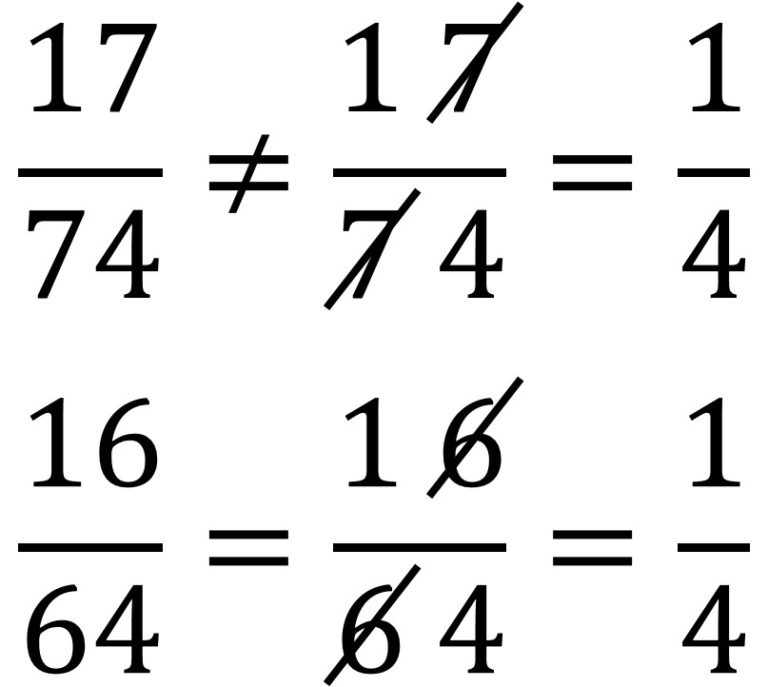
Una vez que hemos entendido cuando una fracción (consideraremos las fracciones propias, es decir, aquellas cuyo valor es menor que 1, lo cual se produce si el numerador es menor que el denominador) es una cancelación anómala, podemos buscar más ejemplos de las mismas. Así, nos planteamos el siguiente problema: encontrar las cancelaciones anómalas en las que numerador y denominador tengan solo dos dígitos.
Veamos cómo se puede resolver este problema. Buscamos una fracción cuyo numerador tenga dos dígitos, luego sea de la forma ac, por lo que su valor es (a.10 + c), y cuyo denominador, con dos dígitos, tiene que ser de la forma cb, luego su calor es (c.10 + d), para que se produzca la cancelación, por tanto, ac / cb = a / b (como es una fracción propia a es menor que b). Es decir,
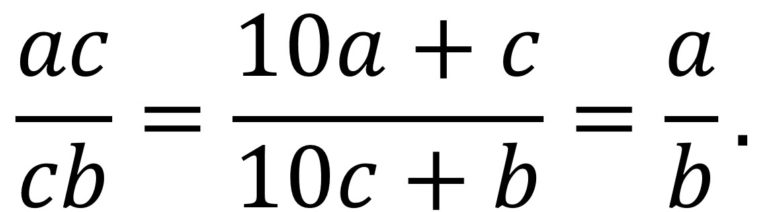
La solución del problema consiste, por lo tanto, en averiguar para qué valores de a, b y c, entre 0 y 9, se satisface la anterior igualdad.
Para empezar, de la igualdad (la segunda) de la expresión matemática anterior, se puede expresar el número que se cancela c en función de los otros dos, a y b.
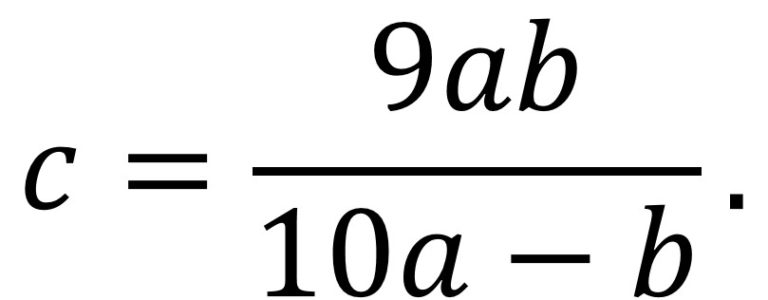
En consecuencia, dados a y b, esa expresión 9 a b / 10 a – b, es un número natural. Más aún, a partir de esa expresión, teniendo en cuenta que c es menor o igual que 9, se puede derivar la siguiente desigualdad.
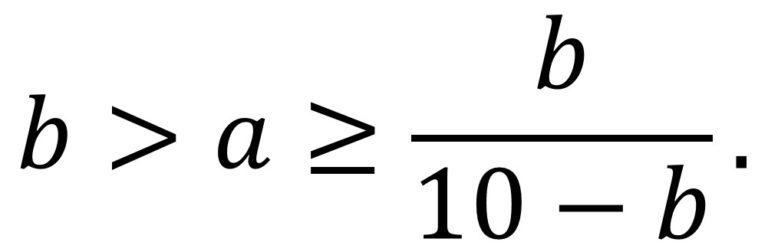
Por lo tanto, se trata de ver para qué números a y b (el primero más pequeño, a < b), tales que verifican la desigualdad anterior, se satisface que el valor calculado anteriormente para c, es decir, 9 a b / 10 a – b, es un número natural. Puede verse fácilmente que las únicas soluciones posibles para el par de número (a, b) son (1, 4), (1, 5), (2,5) y (4,8), que se corresponden con las únicas cancelaciones anómalas con números de dos dígitos.
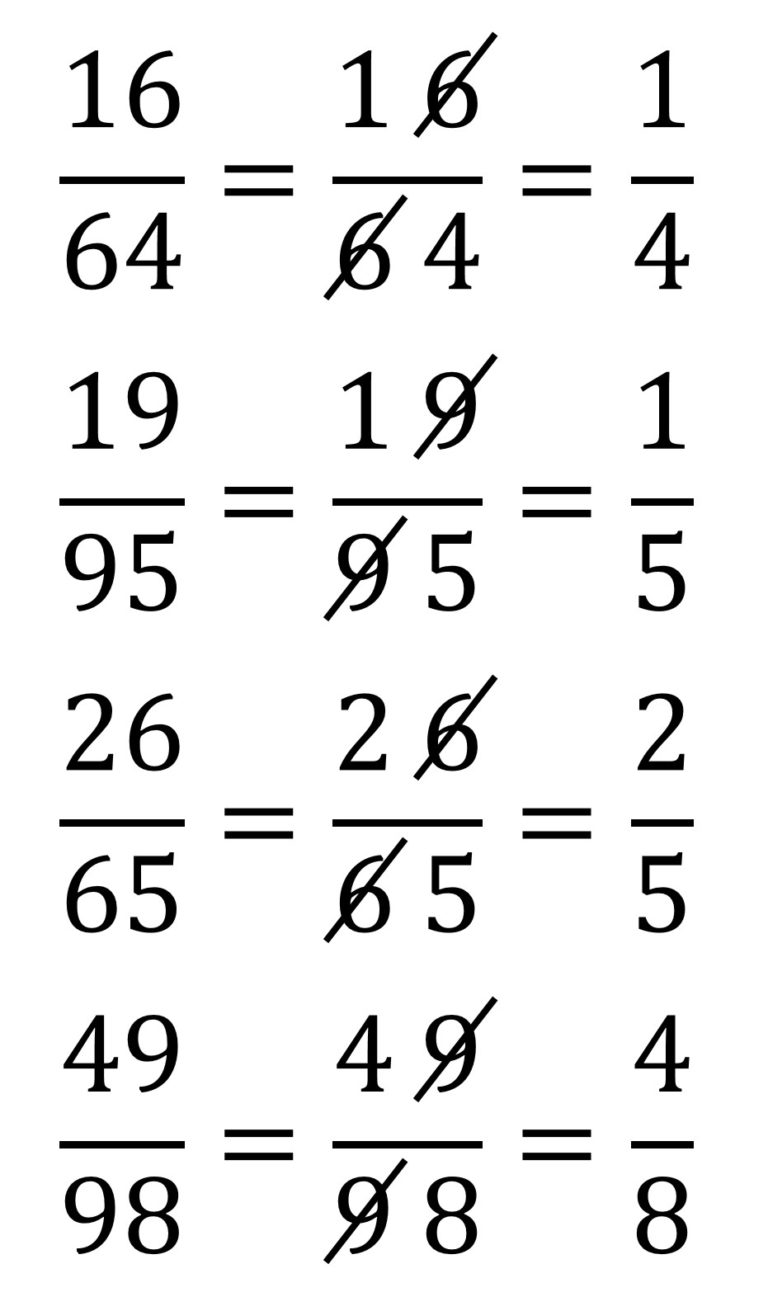
Más aún, a partir de esos cuatro ejemplos sencillos se derivan fácilmente cuatro cadenas de cancelaciones anómalas.

Las primeras menciones, según la literatura matemática, a las cancelaciones anómalas son dos artículos del matemático Alfred Moessner publicados en la revista de la Universidad Yeshiva (Nueva York) Scripta Mathematica, alrededor del año 1950. La siguiente referencia es el artículo Anomalous Cancellation del matemático estadounidense R. P. Boas, publicado en el libro Mathematical Plums (Ross Honsberger (editor). MAA, 1979), en el que se abordaba el problema para números con dos dígitos, pero en una base de numeración arbitraria b. Expliquemos un segundo esto. Teniendo en cuenta que en las cancelaciones anómalas, se “cancelan” dígitos de los números, entonces esta propiedad no depende de los números en sí mismo, sino de su representación en la base de numeración (normalmente la decimal, como hemos estudiado, pero podrían considerarse otras bases).
Pero existen más ejemplos de fracciones propias que son cancelaciones anómalas, con números con más dígitos. Por ejemplo, en el artículo sobre cancelaciones anómalas de la página Wolfram MathWorld se muestran algunas, con números de tres y cuatro dígitos.
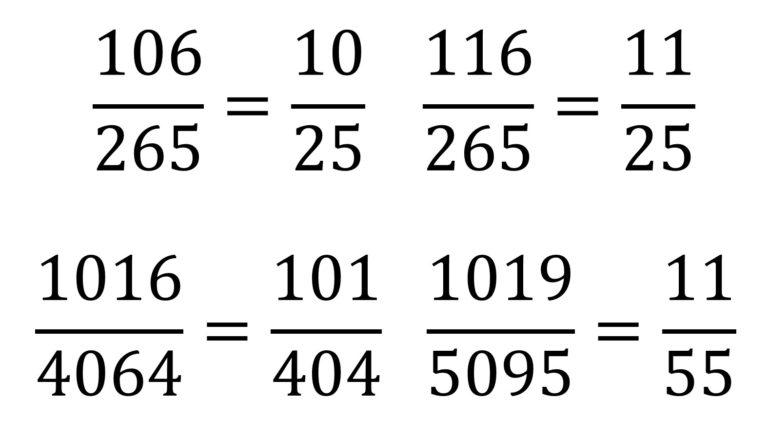
En este último ejemplo se “cancelaban” dos dígitos del numerador y del denominador. Veamos algunos ejemplos más con diferentes características.
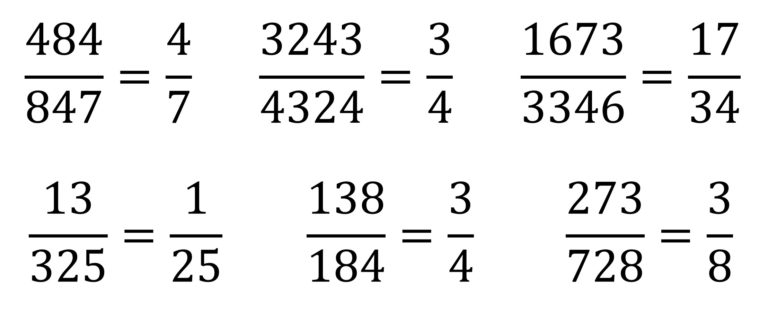
En el libro The Penguin Dictionary of Curious and Interesting Numbers, del matemático y divulgador británico David Wells, se muestra un ejemplo de una cadena con números inicialmente más grandes.

Más aún, en este libro se muestran dos variantes curiosas de cancelaciones, cuando los dígitos que se cancelan son los de las potencias.
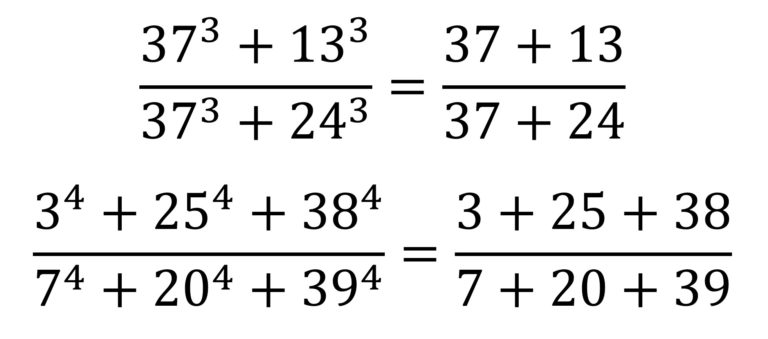
Para terminar, como en otras ocasiones acabaremos con una obra de arte relacionada con los números.

Bibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Press, 1998.
2.- Wolfram MathWorld: Anomalous Cancellation
3.- N. J. A. Sloane, The On-line Encyclopedia of Integer Sequences
4.- Proof Wiki: Anomalous Cancellation on 2-Digit Numbers
5.- Fun with Numbers: Fractions, Anomalous Cancellation
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Francisco Vila
16/64 es 1/4 y no 1/6. El error aparece dos veces distintas en las ilustraciones del artículo.
César Tomé
Yo lo veo correcto. Me permito sugerirle que relea el texto.
jlpg
Lo he releído tres veces y sigo estando de acuerdo con Francisco, 16/64 si cancelas «anómalamente» el 6 tanto en el numerador como en el denominador lo que queda es 1/4 y no 1/6 como pone la ilustración del artículo.
Francisco Vila
Con todo el respeto: usted se equivoca aunque es hasta cierto punto comprensible. Entiendo el artículo y el concepto de cancelación anómala. En general 16/64 no se cancelarían las cifras «6» pero en este caso sí, por eso el resultado es 1/4, ahí está la anomalía. Perfecto.
El problema es que las ilustración dice 16/64 = 1/6 y esto no es una igualdad. Debería decir 16/64 = 1/4 . Le ruego me indique dónde me equivoco o en qué no me he expresado bien.
Gracias
César Tomé
¡Ahora les he entendido! Por favor, refresquen la caché. Estábamos en distintas versiones del artículo. Muchas gracias
jlpg
Gracias a ti.
Francisco Vila
Es muy interesante la manera en que elimina los comentarios ajenos y edita los propios.