El principio del palomar, una potente herramienta matemática (parte 2)

Esta es la segunda parte de una mini serie de dos entradas en la sección Matemoción, del Cuaderno de Cultura Científica, dedicadas al principio del palomar, o de Dirichlet. Como ya comentamos en la entrada anterior, este principio matemático es muy sencillo de formular, no necesita demostrarse, pero al mismo tiempo es una potente herramienta dentro de las matemáticas. Dice lo siguiente: si hay más palomas que palomares, alguno de los palomares deberá contener por lo menos dos palomas. En general, podemos hablar de objetos y cajas donde guardar estos objetos.

En la primera parte vimos algunos ejemplos de su aplicación en problemas relacionados con la vida cotidiana (personas en un teatro con la mismas letras inicial y final en su nombre, número de amigos en una fiesta o sumas de las edades de las personas de una reunión), en teoría de números (algunos resultados sobre divisibilidad) o en geometría (distribución de puntos en un triángulo equilátero), e incluso vimos una generalización del mismo (lo que nos permitió mostrar un ejemplo de coincidencia de cumpleaños).

El ejemplo que se utiliza con más frecuencia en la divulgación científica para explicar la aplicación del principio del palomar a cuestiones más o menos cotidianas, o también como una práctica herramienta para resolver problemas de ingenio, tiene que ver con el número de pelos que tenemos en la cabeza. Aunque me resistía a incluirlo en estas dos entradas por ser un resultado muy conocido, veremos que desde una perspectiva histórica tiene sentido volverlo a recordar.

Ejemplo 1: En Bilbao hay al menos dos personas con el mismo número de pelos en la cabeza.

Para resolver esta cuestión lo primero que tenemos que conocer es cuántos pelos podemos tener como máximo en nuestras cabezas. ¿Lo sabéis? ¿No? No importa, tampoco es una información vital para nuestra existencia. Sin embargo, vamos a realizar una estimación por lo alto de dicha cantidad con el objetivo de utilizarla para resolver este problema.

Supongamos que tenemos cabezas completamente redondas que miden 12 cm. de radio, es decir, unos 75 cm. de perímetro, lo que está al nivel del concurso de cabezones de Kortezubi, en Bizkaia. En tal caso, la superficie de nuestras cabezas, $4 \pi r^2$ , es de unos 1.800 cm². Para realizar una estimación por lo alto, supongamos que tenemos pelos por toda nuestra cabeza, por toda la superficie de esa esfera de 12 cm de radio, y que la densidad del pelo es de 100 pelos por cm², entonces el número de pelos de la cabeza de cualquier persona no va a llegar nunca a los 180.000 pelos. Esta es una estimación por lo alto.

Supongamos que no existe nadie que sea completamente calvo, sin un solo pelo (en caso contrario, además estaría resuelto el problema), por lo tanto, el número de pelos que puede tener una persona va entre 1 y 180.000 (estas cantidades van a ser los palomares para aplicar el principio matemático). Las palomas serán los habitantes de Bilbao, que son unos 350.000. Como hay más bilbaínos que posibles números de pelos, el principio del palomar nos dice que existen al menos dos bilbaínos con el mismo número de pelos en la cabeza.

Hermosa imagen de Bilbao por la noche, sacada de la página “conoce Bilbao conmigo” [http://conocebilbaoconmigo.blogspot.com.es/2014/10/edificios-emblematicos-de-bilbao.html] — Hermosa imagen de Bilbao por la noche, sacada de la página “conoce Bilbao conmigo”

Pero si tenemos en cuenta la generalización del principio del palomar que vimos en la primera entrega dedicada a esta herramienta matemática, podemos obtener un resultado más impactante aún. La generalización dice lo siguiente: si hay n palomas y k palomares (n > k), existe al menos un palomar con al menos (no solo dos, sino) n/k palomas, es decir, el valor máximo es al menos mayor que el valor medio.

Si tenemos en cuenta que el número de habitantes de la Península Ibérica es de al menos 57 millones de habitantes, entonces aplicando el principio del palomar generalizado se obtiene lo siguiente.

Ejemplo 2: En la Península Ibérica hay al menos 317 personas con el mismo número de pelos en la cabeza.

En la entrada anterior habíamos comentado que se atribuye al matemático prusiano Gustav L. Dirichlet (1805-1859), el haber sido la primera persona en aplicar explícitamente este principio matemático, allá por el año 1834, para demostrar un resultado de aproximación de números irracionales mediante racionales. Dirichlet lo llamó Schubfachprinzip (principio de los cajones), y nosotros lo conocemos desde entonces como el principio de Dirichlet.

Sin embargo, en el artículo “The pigeonhole principle, two centuries before Dirichlet” (que me envió Samuel Dalva, a quien le agradezco la información), se explica que la primera referencia al principio del palomar es de dos siglos antes de Dirichlet y tiene que ver con el ejemplo de los pelos de la cabeza.

En el libro, escrito en latín en 1622, Selectae Propositiones del jesuita francés Jean Leurechon, que enseñó matemáticas en la Universidad jesuita de Lorraine en Pont-à-Mousson, se menciona de forma indirecta este principio: “Es necesario que dos hombres tengan el mismo número de pelos, oro y otros”. Además, en el libro Récréation mathematique composee de plusieurs problemes plaisants et facetieux (1624), atribuido al propio Jean Leurechon, se explica por qué “es absolutamente necesario que dos personas tengan el mismo número de pelos”, utilizando el argumento que conocemos como el principio del palomar, si hay más personas que cantidades distintas de pelos que puedan tener, entonces habrá dos con el mismo número de pelos.

Pero volvamos a los ejemplos de aplicaciones de este principio. El primero tiene que ver, de nuevo, con una fiesta, pero esta vez relacionado con el lugar en el que se sientan los comensales en una mesa.

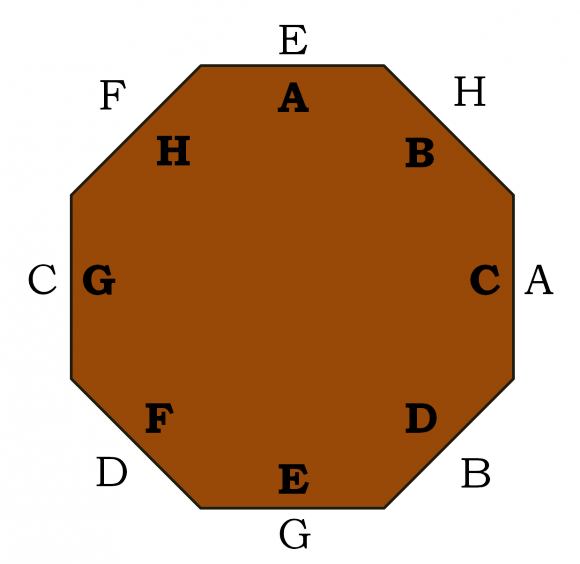
Ejemplo 3: En una fiesta, 8 de los invitados están sentados en una mesa octogonal, con cada uno de los comensales sentado en uno de los lados de la mesa. Cada sitio ha sido asignado a un invitado concreto (marcado con su nombre), sin embargo, los invitados no se han dado cuenta de esta circunstancia y se han sentado al azar. Curiosamente, ninguno de los 8 invitados de esa mesa se ha sentado en el lugar que le correspondía. Vamos a demostrar que hay una forma de rotar la mesa de forma que haya dos personas que quedan sentadas en el sitio correcto.

En la siguiente imagen vemos una posible distribución de las ocho personas sentadas en la mesa octagonal, en la que ninguna de ellos se ha sentado en el sitio que había sido designado para ella.

Para probar la afirmación de que se puede realizar un giro de la mesa en el que al menos dos de los comensales estén sentados en su sitio, vamos a considerar la distancia (en el sentido de las agujas del reloj) de cada una de las personas al sitio que le había sido asignado. Como cada persona está sentada en un lugar incorrecto, entonces las posibles distancias de cada persona a su lugar correcto son {1, 2, 3, 4, 5, 6, 7}.

Pero hay 8 personas que se sientan a la mesa, y 7 posibles distancias de ellas a su sitio correcto (en el sentido de las agujas del reloj), luego por el principio de los cajones, habrá dos personas que estén a la misma distancia (en el sentido de las agujas del reloj) del lugar que tiene escrito su nombre. Por lo tanto, rotando la mesa (en el sentido contrario a las agujas del reloj) tantas posiciones como la distancia que comparten esas dos personas, situará la mesa de tal forma que esas dos personas estén colocadas en el lugar correcto.

Distribución de las ocho personas sentadas en la mesa octagonal, en la que ninguna de ellos se ha sentado en el sitio que había sido designado para ella. Si se giran cuatro posiciones los comensales C y E quedarán sentados en su sitio

El siguiente es un ejemplo interesante, con un argumento sencillo, pero curioso.

Ejemplo 4: Una joven que quiere participar en la Olimpiada Matemática decide entrenarse en la resolución de problemas matemáticos. Durante un periodo de 61 días (dos meses) va a estar haciendo problemas, por lo menos un problema al día, pero no más de 92 problemas (que es la cantidad total que tiene el libro que utiliza). Independientemente de la cantidad de problemas que decida hacer cada día, va a existir una cantidad de días consecutivos durante los cuales realiza exactamente 29 problemas.

Si denotamos por $s_k$ la cantidad de problemas realizados hasta el día $k$ , es decir, la cantidad de problemas acumulados desde el primer día, entonces tenemos que

$0 < s_1 < s_2 < \cdots < s_{61}\leq 92$

Los 61 números $s_k$ son distintos, y están ordenados en orden creciente, puesto que todos los días hace por lo menos un problema.

Con esta notación, lo que tenemos que demostrar es que existen dos días $i$ y $j$ tales que $s_i + 29 = s_j$ (es decir, hay un periodo de $j - i$ días consecutivos en los que ha realizado 29 ejercicios). Por lo tanto, vamos a sumar 29 a todas las sumas acumuladas anteriores, esto es,

$29 < t_1 = s_1 + 29 < t_2 = s_2 + 29 < \cdots < t_61 = s_{61} + 29 \leq 121$

Por la misma razón de antes, estos 61 números $t_k$ son distintos y están ordenados en orden creciente. Las dos desigualdades nos están diciendo que hay 122 números ( $s_1, s_2, \cdots , s_{61}$ y $t_1, t_2, \cdots , t_{61}$ ) que toman valores entre los números 1 y 121. Como tenemos más números (122) que posibles valores (121), eso quiere decir que al menos dos números tienen el mismo valor, es decir, son iguales. Pero, resulta que los 61 primeros números, $0 < s_1 < s_2 < \cdots < s_{61}$ , son diferentes entre sí, al igual que los otros 61, $t_1 < t_2 < \cdots < t_{61}$ , de manera que los dos números que son iguales deberán pertenecer uno al primer grupo y el otro al segundo, es decir, existirá un $j$ , lo que significa un elemento del primer grupo de números $s_j$ , y un $i$ , lo que significa un elemento del segundo grupo de números $t_i = s_i + 29$ , tales que $s_j = s_i + 29$ , como deseábamos.

Logotipo de la Olimpiada Internacional de Matemáticas

Como ya comentamos en la entrada anterior del Cuaderno de Cultura Científica dedicada a este tema, el principio de Dirichlet tiene muchas aplicaciones a la teoría de números. Empecemos con algunos resultados sencillos.

Ejemplo 5: Dado un número natural n cualquiera (da igual que sea el 37, el 158 o el 453), existe un número cuyos dígitos son solamente 5s y 0s, que es divisible por ese número n.

Este es un ejemplo que me gusta porque aunque no es un gran resultado, es bastante sorprendente. Tenemos que encontrar un número que sea divisible por el número n que hemos elegido. Si habéis leído la anterior entrada dedicada al principio de Dirichlet, recordaréis un resultado de divisibilidad por el número elegido, exactamente “dados n+1 números naturales, se pueden encontrar dos cuya diferencia sea divisible por n” (bueno, lo probamos para el caso particular de los números n + 1 = 47 y n = 46). Ahora vamos a apoyarnos en este resultado.

Necesitamos por lo tanto n + 1 números, cuya diferencia de dos de ellos esté compuesta solo por las cifras 5 y 0. Por ejemplo, podemos tomar los n + 1 números siguientes: 5, 55, 555, 5555,… y así hasta el número formado por n+1 dígitos. Por el resultado anterior, existen dos cuya diferencia, que estará formada por 5s y 0s, es divisible por n.

La gran rueda (1920-21), de Laszlo Moholy-Nagi

Ejemplo 6: Consideremos los enteros del 1 al 10 distribuidos al azar (es decir, en cualquier orden) en una circunferencia, entonces existirán tres números vecinos cuya suma sea al menos 17.

Denotemos los números, según aparecen en la circunferencia y en el sentido de las agujas del reloj, $x_1, x_2, \cdots, x_{10}$ , y denotemos las sumas posibles de tres números vecinos como $s_1 = x_1 + x_2 + x_3$ , $s_2 = x_2 + x_3 + x_4$ , \cdots , $s_9 = x_9 + x_{10} + x_1$ , $s_{10} = x_{10} + x_1 + x_2$ .

La suma de los diez números $x_1, x_2, \cdots, x_{10}$ , es 55, puesto que realmente es la suma de los 10 primeros números. En consecuencia, la suma de todas las sumas de tres vecinos es 165, puesto que cada término $x_i$ aparece sumado tres veces, es decir, $s_1 + s_2 +\cdots + s_{10} = 165$ .

El principio de Dirichlet generalizado, donde las sumas parciales $s_1, s_2,\cdots, s_{10}$ son los palomares y las palomas serían las 165 unidades que suman la cantidad 165, nos dice que por lo menos habrá una de esas sumas cuyo valor será al menos 165/10 = 16,5, es decir, habrá una suma $s_i = s_i + s_{i+1} + s_{i+2}$ que suma por lo menos 17.

Puede demostrarse que también hay una suma parcial de tres términos vecinos que suman al menos 18. El argumento es similar. Se quita el número 1, y los otros 9 números se separan en tres grupos disjuntos de tres números vecinos. La suma de estos es 54, pero hay tres sumas de tres vecinos, y como 54/3 = 18, entonces alguna de las tres sumas vale al menos 18.

Sin embargo, el resultado ya no es válido para 19, y un ejemplo es la siguiente distribución de los diez primeros números sobre la circunferencia: 1, 10, 6, 2, 9, 5, 4, 8, 3, 7. Se obtiene 18 tres veces 10 + 6 + 2, 9 + 5 + 4 y 8 + 3 + 7, pero no 19.

A continuación, vamos a mostrar un resultado algo más complejo, pero de mayor importancia matemática. Este se debe a los matemáticos húngaros Paul Erdös (1913-1996) y Georges Szekeres (1911-2005), científicos que ya aparecieron en la anterior entrada.

Ejemplo 7: Sea una secuencia de $nm+1$ números reales, entonces o bien existe (leídos de izquierda a derecha) una sucesión creciente de al menos $n+1$ números, o una sucesión decreciente de al menos $m+1$ números.

Para entender un poco mejor este problema e intentar caminar hacia la solución, vamos a analizar un caso concreto. Supongamos que n = m = 3, y sean, por ejemplo, los diez números siguientes: 37, 59, 91, 24, 16, 84, 5, 63, 45, 77.

Relacionado con nuestro objetivo, nos interesa conocer como son las sucesiones decrecientes de números del listado anterior (leído de izquierda a derecha), así como las crecientes: Por este motivo, vamos a contar que sucesiones decrecientes, y crecientes, hay, pero que terminen en cada uno de los números del listado inicial.

Tabla con las sucesiones decrecientes más largas que terminan en los diferentes números x de nuestro listado inicial de 10 números

Como vemos, existen dos sucesiones decrecientes de cuatro elementos, luego satisfacen la condición de tener al menos 4 (= 3 +1) números.

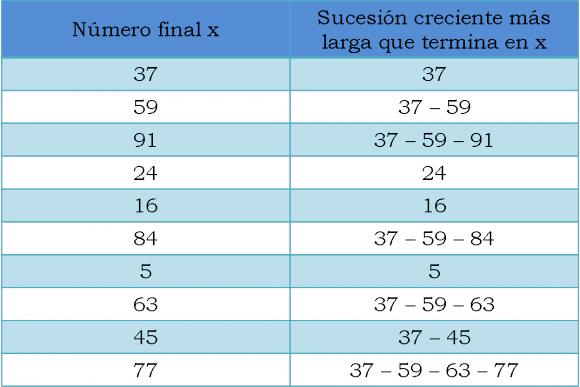
Tabla con las sucesiones crecientes más largas que terminan en los diferentes números x de nuestro listado inicial de 10 números

Existe una sucesión crecientes de cuatro elementos, luego satisface la condición de tener al menos 4 (= 3 +1) números.

A continuación, podemos comparar, para cada número x, las longitudes de las máximas sucesiones decrecientes, y crecientes, que terminan en ese número x.

Hasta aquí la información que hemos obtenido de este ejemplo, y la observación de que se cumple el resultado anunciado en este ejemplo. Pero, una idea para recoger toda esta última información de una forma gráfica es representar la información de las longitudes de las máximas sucesiones decrecientes, y crecientes, que terminan en cada número como pares de coordenadas de puntos del plano. Así, los datos de la anterior tabla se corresponden con los siguientes puntos del plano.

El cuadro anterior nos ofrece una idea para demostrar el resultado. Veámoslo. Sean $x_1, x_2, \cdots, x_{nm+1}$ el listado de $nm+1$ números naturales dados inicialmente. Denotamos por $a_i$ la longitud de la sucesión decreciente más larga que acaba en $x_i$ , por $b_i$ la longitud de la sucesión creciente más larga que acaba en $x_i$ , y consideremos los pares de estos números $(a_i, b_i)$ .

Ahora, si no se cumpliera el resultado, eso querría decir que las longitudes más largas de las sucesiones decrecientes serían menores que m, es decir, $1\leq a_i\leq m$ , y que las longitudes más largas de las sucesiones crecientes serían menores que n, es decir, $1\leq b_i\leq n$ . Entonces, como mucho hay $nm$ pares $(a,b)$ , que son los palomares que necesitamos para aplicar el principio de Dirichlet.

Ahora, como tenemos $nm+1$ números $x_k$ , que son nuestras palomas, entonces por el principio que estamos analizando habrá dos números $x_i$ y $x_j$ ( $i < j$ ) distintos cuyos pares asociados serán iguales, $(a_i,b_i) = (a_j,b_j)$ .

Pero veremos que esto no es posible. Sea $i < j$ . Si $x_j < x_i$ , entonces tomamos la sucesión decreciente más larga que termina en $x_i$ , y le añadimos el número $x_j$ , que tendrá un elemento más, luego $a_j$ será al menos $a_i+1$ , y entonces $a_j > a_i$ , luego los pares asociados $(a_i,b_i)$ y $(a_j,b_j)$ son distintos. Por el contrario, si $x_j > x_i$ , y consideramos la sucesión creciente más larga que termina en $x_i$ , entonces añadiéndole $x_j$ , se obtendrá un elemento más y $b_j > b_i$ , luego también en este caso los pares asociados $(a_i,b_i)$ y $(a_j,b_j)$ son distintos.

En consecuencia, como no puede haber dos pares $(a_i,b_i)$ y $(a_j,b_j)$ iguales, hemos hecho una suposición falsa, es decir, o bien existe (leídos de izquierda a derecha) una sucesión creciente de al menos $n+1$ números, o una sucesión decreciente de al menos $m+1$ números.

Recordad que si tenemos más coches rojos de juguete que cajones en los que guardarlos, habrá por lo menos dos coches rojos de juguete que estarán guardados en el mismo cajón

Mi intención inicial al empezar esta segunda entrada dedicada al principio del palomar era terminar con la aplicación del mismo realizada por Dirichlet en 1834, para aproximar números irracionales por medio de números racionales. Sin embargo, como me ocurre en muchas ocasiones, me emociono con el texto y me olvido de que el espacio es limitado. Por lo tanto, dejaremos ese ejemplo para alguna otra ocasión que volvamos a interesarnos por el principio del palomar, así como alguno de los ejemplos geométricos que también se me han quedado en el tintero. Espero que hayáis disfrutado de la entrada.

Bibliografía

1.- Dimitri Fomin, Sergey Genkin, Ilia Itenberg, Círculos matemáticos, Biblioteca de Estímulos Matemáticos, SM-RSME, 2012.

2.- R. B. J. T. Allenby, Alan Slomson, How to count, an introduction to combinatorics, CRC Press, 2011.

3.- Benôit Rittaud, Albrecht Heeffer, The pigeonhole principle, two centuries before Dirichlet, The mathematical intelligencer 36, 2014.

4.- Mark Flanagan, The pigeonhole principle, School of Electrical, Electronic and Communications Engineering, University College Dublin.

5.- Harm Derksen, Mathematical problem solving

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Esta entrada participa en la Edición 6.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.

Próximos eventos

La exposición Surf y Ciencia en Bilbao

¿Alguna vez te has preguntado cómo consiguen los y las surfistas deslizarse sobre las olas? ¿Sabes cómo se forman las olas? El surf es un deporte tras el que, como queda en evidencia en esta exposición, hay mucha ciencia. En la muestra Surf y Ciencia se explica la relación entre…

6 de noviembre, 2024–12 de diciembre, 2024

Bizkaia Aretoa UPV/EHU

Avenida Abandoibarra, 3, Bilbao

El conocimiento científico y los bertsos se unen en la Semana del Euskera

Con motivo de la Semana del Euskera la Dirección de Promoción del Euskara de la UPV/EHU, la Cátedra de Cultura Científica de la UPV/EHU y la Bilbioteca Bidebarrieta han organizado una nueva edición de Bertsozientzia. En el programa conducido por Idoia Torregarai el bertsolarismo y el conocimiento científico se unirán…

4 de diciembre, 2024

Biblioteca Bidebarrieta

Calle Bidebarrieta, 4, Bilbao

5 comentarios

El principio del palomar, una potente herramien… 25 de febrero, 2015

[…] Esta es la segunda parte de una mini serie de dos entradas en la sección Matemoción, del Cuaderno de Cultura Científica, dedicadas al principio del palomar, o de Dirichlet. Como ya comentamos en la entrada anterior, este principio […]
El principio del palomar, una potente herramien… 25 de febrero, 2015

[…] Esta es la segunda parte de una mini serie de dos entradas en la sección Matemoción, del Cuaderno de Cultura Científica, dedicadas al principio del palomar, o de Dirichlet. […]
Javier Novoa 25 de febrero, 2015

«este principio matemático es muy sencillo de formular, no necesita demostrarse» <- más de un matemático estricto habrá levantado la ceja al leer esto…. XD

Responder
Una de mates: El principio del palomar | Una de mates | Cuaderno de Cultura Científica 11 de octubre, 2015

[…] El principio del palomar, una potente herramienta matemática (parte 1 y 2) […]
El juego del Sim – Cuaderno de Cultura Científica 1 de mayo, 2017

[…] b) El principio del palomar, una potente herramienta matemática (parte 2) […]