
MI HIJO Y YO LE LLAMÁBAMOS PROFESOR. Y el profesor llamaba a mi hijo “Root”, porque su coronilla era tan plana como el signo de la raíz cuadrada.
– Vaya, vaya. Parece que aquí debajo hay un corazón bastante inteligente –había dicho el profesor mientras le acariciaba la cabeza sin preocuparse de que se le despeinara.
Mi hijo, que llevaba siempre una gorra para que sus amigos no se burlasen de él, metió la cabeza entre los hombros, a la defensiva.
– Utilizándolo, se puede dar una verdadera identidad a los números infinitos, así como a los imaginarios.
Y dibujó el signo de la raíz cuadrada con el dedo índice en el borde de su escritorio, sobre el polvo acumulado: (signo de la raíz cuadrada).
Entre las innumerables cosas que el profesor nos enseñó a mi hijo y a mí, el significado de la raíz cuadrada ocupa un lugar importante.
Este es el inicio de un excelente libro, al que vamos a dedicar la entrada de esta semana de la sección Matemoción del Cuaderno de Cultura Científica. Una de las novelas más interesantes que he leído en los últimos años y que suelo recomendar a todas aquellas personas interesadas en literatura relacionada con las matemáticas, y al resto, también. Se trata de la novela “La fórmula preferida del profesor” (funambulista, 2008), de la escritora japonesa Yoko Ogawa.

La fórmula preferida del profesor (博士の愛した数式, hakase no ai shita suushiki) fue publicada originalmente en Japón en 2003 (por la editorial Shichosha), con un gran éxito entre el público, más de un millón de copias vendidas en dos meses, hasta alcanzar los dos millones y medio, y reconocida también por la crítica. Recibió el Premio Yomiuri en 2003, el Premio de las Librerías Japonesas en 2004, así como el Premio de la Sociedad Japonesa de Matemáticas, “por haber mostrado la belleza de esta disciplina”. Tras el éxito de la novela se realizaron adaptaciones al cine (The professor’s beloved equation, Takashi Koizumi, 2006), al teatro, a la radio y al cómic.

Esta novela, que ha sido traducida a varios idiomas, entre ellos inglés, francés, español, italiano, griego, alemán, coreano o thai, lanzó a su autora a la fama internacional, para acabar convirtiéndose con el tiempo en uno de los grandes escritores de la literatura contemporánea.

La relación entre los tres personajes principales, el profesor, la asistenta y “root”, el hijo de esta (por cierto, que los personajes creados por Ogawa para esta historia no tienen nombre propio), es el tema central de esta novela. La “asistenta”, que es la narradora, es una joven mujer, madre soltera de un hijo de 10 años, que entra a trabajar como asistenta de un viejo y enfermo profesor de matemáticas. Ella limpia el lugar en el que vive el profesor, cocina para él y en general atiende sus necesidades cotidianas. El “profesor” tiene 64 años, antes era un profesor universitario experto en Teoría de Números y 17 años atrás (en 1975) sufrió un accidente de tráfico, como consecuencia del cual se dañó su cerebro. Su memoria se paró en el momento del accidente y solo tiene recuerdos de su vida anterior. A partir de ese momento, su memoria solo tendrá una autonomía de 80 minutos. Es decir, solo recuerda lo que va sucediendo en los 80 últimos minutos de su vida. Por este motivo, apunta todo lo que cree necesario en pequeños papeles que cuelga con imperdibles de su ropa (o coloca en los lugares donde los necesita), “mi memoria solo dura 80 minutos”, “la nueva asistenta” (acompañado de un dibujo de una cara de mujer) o “Hilbert, decimo tercer problema…”, “fracaso del método analítico…”. “Root”, el hijo de la asistenta, va todas las tardes, después del colegio, a casa del profesor a hacer los deberes y a esperar que su madre termine de trabajar, ya que ella no tiene con quien dejarlo. A lo largo de esta historia, el profesor se irá convirtiendo en padre y abuelo, en maestro y divulgador de las matemáticas, la asistenta en hija, en alumna y simboliza en cierta medida al público, y Root en nieto, alumno y amigo.

Esta novela nos habla de la soledad, y del sufrimiento que causa, de las relaciones humanas, de la amistad, de los extraños compañeros que puede tener y su fuerza liberadora, del amor o del peso del pasado, pero también de lo que pueden aportar ancianos y enfermos a una sociedad que los considera inútiles. Todo ello con gran delicadeza, sentimiento y optimismo.
En esta historia no solo nos encontramos con las matemáticas formando parte de su argumento, sino que nos encontramos ante un excelente ejercicio de divulgación matemática. Existen dos niveles de divulgación de las matemáticas en esta obra, uno interno desarrollado por el profesor, fundamentalmente hacia la asistenta, y otro externo, que tiene como objetivo al lector. Tal fue el éxito de la divulgación matemática contenida en este libro que su autora y el matemático Masahiko Fujiwara escribieron el libro “Una introducción a las matemáticas más elegantes” (en japonés).

-¿Qué número de pie calzas?
Lo primero que me preguntó al decirle que yo era su nueva asistenta no fue mi nombre, sino qué número de pie calzaba. No me saluadó, ni de palabra ni con un gesto. Yo, siguiendo la regla de oro de toda asistenta, según la cual no se puede responder con una pregunta, contesté a su pregunta:
-El 24.
-Vaya, es un número muy resuelto, la verdad. Es el factorial de 4.
El profesor cerró los ojos con los brazos cruzados. El silencio se mantuvo durante un momento.
-¿Qué es el factorial?
No sé por qué se lo pregunté, pero pensé que sería oportuno seguir hablando un poco más de aquello, ya que, al parecer, el número del calzado iba a ser algo importante para mi empleador.
-Si multiplicamos los números naturales, del 1 al 4, nos da 24 -contestó el profesor sin abrir los ojos-. ¿Cuál es tu número de teléfono?
-Es el 567 14 55.
-¿El 5671455? ¡Vaya maravilla! ¡ Es igual a la cantidad de números primos que existen hasta cien millones!
El profesor iba asintiendo con la cabeza, como si estuviera muy contento.
Aunque no entendí cómo ni por qué era maravilloso mi número de teléfono, […]Unos días después de acudir regularmente al pabellón como asistenta, me di cuenta de que el profesor, cuando estaba confuso, sin saber qué decir, tenía la manía de hablar con números en lugar de palabras. Era la manera que había ingeniado para comunicarse con los demás. […]
Hasta que dejé de ser su asistenta, repetimos cada mañana, en la entrada, la conversación de los números.
Analicemos brevemente la relación de cada uno de los tres personajes con las matemáticas. El “profesor” estudió matemáticas en la Universidad de Cambridge, después realizó su tesis doctoral sobre “Teoría de Números Trascendentes”, por la que fue premiado, tras lo cual empezó a trabajar en un “instituto universitario de investigaciones matemáticas” en Japón, llegando a ser “catedrático especialista en Teoría de Números”.
Cuando el profesor habla de su investigación menciona que en Cambridge “me ocupaba de la teoría de Artin sobre las formas cúbicas con coeficientes enteros. Basándome en la idea llamada método del círculo, utilicé la geometría algebraica, la teoría de los números enteros y la aproximación diofántica… Intenté hallar el camino intermedio, una fórmula aún no descubierta por las conjeturas de Artin”. Sin embargo, estas expresiones matemáticas complicadas no se explican en el libro, simplemente tienen el objetivo de intentar transmitir la complejidad de la investigación matemática de alto nivel, en este caso en el área de la Teoría de Números. De hecho, la asistenta tras escuchar un intento de explicación del profesor del tema de su tesis, menciona que “Había cifras, letras y signos misteriosos que formaban una serie continua. No entendí ni una sola de las palabras que pronunció, y sin embargo comprendí que allí había una lógica imparable y que el profesor avanzaba en medio de ella”. Las matemáticas son un lenguaje abstracto, que si no se conoce es complejo. Así mismo, cuando la asistenta cotillea el interior de la tesis del profesor, de la primera página solamente entiende la expresión “chapter 1”.
Entre los libros de matemáticas que tiene el profesor en sus estanterías se mencionan los títulos Teoría del Grupo Matemático Continuo, Teoría de los Enteros Algebraicos, Investigación sobre la Teoría de los Números (sin embargo, en la versión en inglés los títulos son Group Theory, Algebraic Number Theory, Studies in Number Theory), así como los autores Chevalley (Claude Clevalley, 1909-1984,fue un matemático francés, miembro del grupo Bourbaki y especialista en Teoría de Números y Geometría Algebraica), Hamilton (William R. Hamilton, 1805-1865, matemático, físico y astrónomo irlandés, fue uno de los grandes científicos del siglo XIX, que introdujo la mecánica hamiltoniana, una reformulación de la mecánica clásica, así mismo introdujo el concepto matemático de cuaternión), Turing (el matemático inglés Alan Turing, 1912-1954, famoso por descifrar los códigos nazis durante la segunda guerra mundial, en particular la máquina enigma, pero cuyas otras contribuciones fuera de la criptografía también fueron revolucionarias, considerado el padre de las ciencias de la computación, introdujo el concepto de máquina de Turing, trabajó en morfogénesis dentro de la biología matemática, o en cibernética), Hardy (Godfrey H. Hardy, 1877-1947, fue un matemático inglés que trabajó en Teoría de Números y Análisis Matemático, autor del libro Apología de un matemático, su nombre está ligado al del matemático indio Srinivasa Ramanujan) y Baker, todos ellos grandes matemáticos. Seguramente el matemático inglés y medalla Fields Alan Baker, nacido en 1939, sea el menos conocido de los mencionados, aunque por otra parte su investigación es la más cercana a la del profesor de la novela (ecuaciones diofánticas, teoría de números trascendentes, etc).
Debido a su enfermedad, a los tan solo 80 minutos de autonomía de su memoria, el profesor ya no puede realizar una investigación matemática en Teoría de Números, por lo que dedica su tiempo y sus fuerzas a resolver problemas matemáticos que plantean algunas revistas para aficionados a esta ciencia. En cualquier caso, a través de este trabajo realizado por el profesor, el lector, o lectora, puede acercarse un poco a la forma de trabajar de los matemáticos y matemáticas, al menos de los matemáticos puros. Las herramientas que utiliza el profesor, y las personas que investigan en esta ciencia en general, son lápiz y papel (o también, tiza y pizarra), así como libros y revistas matemáticas que son utilizados para consultar lo ya descubierto y demostrado, y por supuesto, la herramienta fundamental, el cerebro del investigador. Aunque hemos de decir que a esa breve relación de herramientas clásicas que se utilizan en la investigación matemática, al menos la pura, le falta un par de herramientas modernas indispensables, como son el ordenador e internet.

Para superar el problema de la autonomía de 80 minutos de su memoria, el profesor apunta en notas y en cuadernos los avances que va realizando en la resolución del problema que intenta resolver, para no olvidarlos. Lo cual es una buena metáfora de la historia de la investigación matemática. Cada matemático investiga apoyándose en los resultados que han investigado otros antes que él, y para poder desarrollar su investigación primero hay que leer y estudiar lo que han hecho otros investigadores antes. Así, cada día y cada vez que se pone a trabajar, el profesor deberá leer las notas que ha ido apuntando en sus cuadernos.
En relación a las matemáticas, la “asistenta” representaría al público general. En la escuela las odiaba “hasta el punto de sentir escalofríos sólo con ver los manuales”. Sin embargo, las sencillas e interesantes explicaciones que le ofrece el profesor de diferentes temas matemáticos, en particular, relacionados con los números, acaban haciendo que se interese cada vez más por ellas, llegando a ser incluso matemáticamente activa. Lo cual se debe a la buena divulgación que realiza el profesor, un ejemplo a seguir.
“Root” representa al alumno, más que al público. El profesor le va inculcando el interés por las matemáticas y dedica mucho de su tiempo a enseñarle la resolución de problemas. El interés de Root va creciendo hasta el punto que de mayor acabará estudiando matemáticas y convirtiéndose en profesor de enseñanza secundaria.

Muchos son los temas matemáticos tratados por el profesor/Yoko Ogawa, algunos de los cuales ya empiezan a ser clásicas referencias en la literatura contemporánea relacionada con las matemáticas. Raíces cuadradas, números imaginarios, números amigos, es decir, dos números tales que la suma de los divisores de cada uno de ellos da el otro, por ejemplo,
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284 y
1 + 2 + 4 + 71 + 142 = 220,
números perfectos, que son amigos de sí mismos (6, 28, 496), matemáticos como Fermat, Descartes o Pitágoras, la fórmula de la suma de los n primeros números,
1 + 2 + … + n = 1/2 n (n+1)
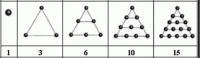
pero no se explica la fórmula sin más, sino que el lector va acompañando a la asistenta en sus diversos intentos de demostrarla hasta que finalmente lo consigue (con ello Ogawa muestra que el trabajo de los matemáticos no es lineal, sino una búsqueda, siendo el error parte de la misma; así mismo anima a las personas a ser matemáticamente activas), números primos (en particular, los primos gemelos y los de Mersenne), números triangulares (obtenidos al colocar piedras en forma triangular, 1, 3, 6, 10, 15),
y mediante los cuales se puede realizar una demostración visual de la fórmula anterior,

la fórmula de Euler, eπi +1 = 0 , considerada la ecuación más bella de la ciencia (sencilla, con gran significado matemático y que implica importantes constantes matemáticas), el último teorema de Fermat y la demostración de Andrew Wiles, los números π, e y 0, etc, todo ello bien explicado, bien integrado en la narración, e interesando al lector a través de la relación de los personajes.
Mientras que en esta entrada nos hemos centrado en aspectos más generales, en una futura entrada del Cuaderno de Cultura Científica desarrollaremos algunos de los temas matemáticos que aparecen en la novela “La fórmula preferida del profesor”.
Al darse cuenta de que el número de su asiento era 7-14 y el de Root era 7-15, empezó a hablar sobre los dos números, olvidándose de sentarse:
—El 714 es el número del récord de home runs que estableció Babe Ruth en 1935. El 8 de abril de 1974, Hank Aaron bateó su 715º home run al lanzador Al Downing de los Dodgers. El producto de 714 por 715 equivale a la multiplicación de los primeros siete números primos.
714 × 715 = 2 × 3 × 5 × 7 × 11 × 13 × 17 = 510510
O bien, la suma de los factores primos de 714 es igual a la suma de los factores primos de 715.
714 = 2 × 3 × 7 × 17
715 = 5 × 11 × 13
2 + 3 + 7 + 17 = 5 + 11 + 13 = 29
Hay muy pocos pares consecutivos de números enteros que tengan esta propiedad. Sólo existen 26 pares por debajo de 20000. Es la pareja Ruth-Aaron. Igual que con los números primos, cuanto más altos son los números, menos hay. Por cierto, el más pequeño es el 5 y el 6, sabes…
Demostrar si existen infinitamente o no es bastante complicado. Pero lo más importante es que yo me siento en el asiento 7-14 y tú te sientas el 7-15. Jamás podrá ser al revés. Son los nuevos quienes baten el récord antiguo. Es razonable que sea así. ¿No te parece?
Esta no es la única novela de la escritora japonesa Yoko Ogawa relacionada con las matemáticas. Uno de los protagonistas de la novela Perfume de hielo (funambulista, 2009) es un joven que en su niñez demostró ser un genio de las matemáticas, y que ganaba numerosos concursos matemáticos.
Y en el relato largo La residencia de estudiantes (funambulista, 2011), hay un personaje secundario que es estudiante de matemáticas.
Bibliografía
1.- Yoko Ogawa, La fórmula preferida del profesor, editorial funambulista, 2008.
2.- Jose María Sorando, La ecuación preferida del profesor, Matemáticas y Cine
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica


ununcuadio
Me has recordado lo que disfruté leyendo este libro 🙂
Raúl Ibáñez
Me alegro mucho… para mí también fue una gozada leerlo… 🙂
Begoña Suarez
¡Una maravilla de libro! Muy recomendable
Raúl Ibáñez
😉
Esti
Raúl, muchas gracias por este post.
Me maravilló el libro, y me han entrado ganas de releerlo. Además, en tu artículo he descubierto que hay película. Más no se puede pedir;)
Cinema & Matemàtiques | Departament de Matemàtiques de l'Escola Sadako
[…] Aquesta pel·lícula està basada en el llibre del mateix títol que va rebre molt bones crítiques per exemple en el Cuaderno de cultura científica. […]