Hace un par de semanas me llegó a través de twitter el nombre un artista menorquín, Carles Gomila, y como soy una persona curiosa me metí en su página web para descubrir un arte hermoso y muy interesante, cuadros de una gran belleza centrados fundamentalmente en la figura de la mujer (a modo de ejemplo, os dejo el nombre de algunas de sus series de pinturas, Miss Medusa, Venus Reload, Retrodivas, Like a Virgin o Japanese odyssey), con una estética que puede enmarcarse dentro del surrealismo mágico. Entre sus cuadros descubrí este que llamó mi atención…

… ya que Lady Komiki sostenía en su mano un poliedro muy interesante, el rombododecaedro estrellado. Pero el color elegido por Carles Gomila para este objeto me hizo pensar en un puzzle geométrico tridimensional que se encuentra entre mis favoritos, es un puzzle basado en la descomposición en seis piezas iguales del rombododecaedro estrellado. Y entonces lo vi claro, mi siguiente entrada del Cuaderno de Cultura Científica tenía que ser sobre este poliedro estrellado y el puzzle que se basa en el mismo.

Vamos a empezar por el poliedro convexo sobre el que se construye nuestro “objeto de deseo”, el rombododecaedro. Primero, recordemos que un poliedro es convexo si dados dos puntos cualesquiera del mismo, el segmento que los une está completamente en su interior (incluida la superficie), o dicho de otra forma, no hay espacio exterior entre puntos del poliedro. En consecuencia, estos poliedros no tienen zonas que sobresalgan en exceso, como sería el caso de un poliedro estrellado, ni zonas exteriores que entran en el poliedro. Una forma equivalente de saber si un poliedro es convexo es ver si todas sus caras pueden apoyarse completamente sobre un plano, por ejemplo, posándolo sobre una mesa.

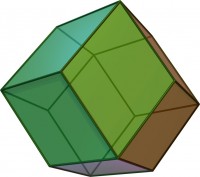
El rombododecaedro es un poliedro convexo con 12 caras iguales con forma de rombo, 24 aristas y 14 vértices, los cuales son de dos tipos (dependiendo de si en ellos se juntan 3 rombos –por la parte de los vértices de ángulos obtusos- o 4 rombos –por la parte de los ángulos agudos-), 6 de un tipo y 8 del otro. Los ángulos de los vértices del rombo son 70º 32’ y 109º 28’. Además, el ángulo entre los planos de dos rombos adyacentes, que se denomina ángulo diédrico, es de 120º.

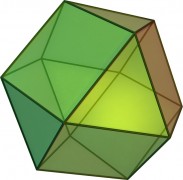
El rombododecaedro es el poliedro dual del cuboctaedro. Este, como vemos en la imagen, es un poliedro convexo formado por 6 cuadrados y 8 triángulos equiláteros, y en cada vértice se juntan 2 cuadrados y 2 triángulos (por este motivo, el cuboctaedro es un sólido arquimediano, es decir, sus caras son polígonos regulares de dos o más tipos y sus vértices son uniformes, en todos ellos se juntan las mismas caras y de igual manera; pero de los sólidos arquimedianos ya hablaremos en otra ocasión).

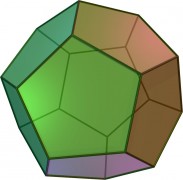
Recordemos ahora que dos poliedros son duales si los vértices de uno se corresponden con las caras del otro, es decir, si consideramos los puntos medios de las caras de uno de los poliedros, y los unimos con aristas, se obtiene el poliedro dual en su interior (en la siguiente imagen puede verse la dualidad de los sólidos platónicos).

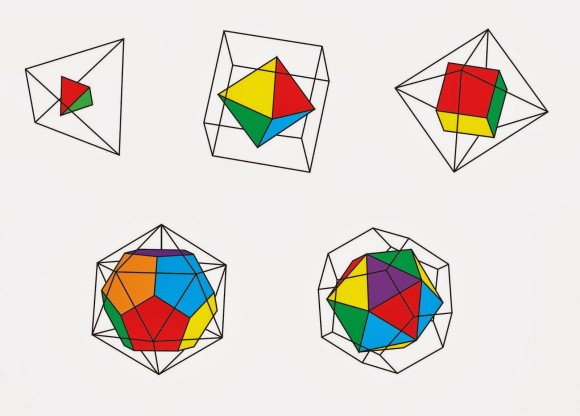
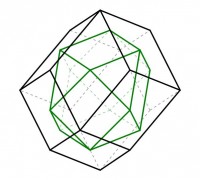
A la familia de poliedros duales de los arquimedianos, como es el caso del rombododecaedro, se les llama sólidos de Catalan (el nombre se debe al matemático belga Eugène Catalan, 1814-1894).

Pero el rombododecaedro no es solamente una bella invención matemática. Nos lo podemos encontrar en la naturaleza ya que, por ejemplo, es el aspecto macroscópico que tienen algunos minerales, como es el caso del granate o la fluorita.

Este poliedro convexo está relacionado con el diseño de los panales de las abejas. Johann Kepler (1571-1630) en su libro Strena seu de nive sexángula (Regalo de año nuevo Sobre el copo de nieve hexagonal), de 1611, reflexionó sobre la forma que tenían los panales de las abejas. Estos están formados por prismas hexagonales pegados unos a otros por sus caras laterales (por lo que, al compartir las paredes, se ahorra en la cera utilizada para su construcción) y sin dejar espacios libres entre ellos (aprovechando bien el espacio), lo cual es posible gracias a que el hexágono es uno de los tres polígonos regulares (junto al triángulo y al cuadrado) que puede teselar el plano, es decir, puede cubrir el plano sin dejar huecos.

Además, de las tres formas de recubrir el plano mediante polígonos regulares, la que utiliza hexágonos es óptima en el sentido de que para un perímetro dado, el hexágono cubre una mayor superficie. En consecuencia, en el prisma hexagonal habrá una relación óptima entre el volumen interior y la superficie de las paredes del prisma. Es decir, para almacenar la misma cantidad de miel se utiliza menos cera para construir las paredes.

Sin embargo, las celdas de los panales de las abejas no son prismas ya que el fondo de las mismas no es plano. Como también comenta Kepler en su libro sobre el copo de nieve, las celdas de los panales acaban en tres planos, con forma de rombo, que se unen por uno de sus ángulos obtusos.

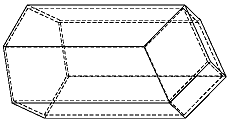
Muchos científicos, en particular en el siglo XVIII (entre otros los matemáticos Maraldi (1665-1729), Reaumur (1683-1757), Johann Samuel König (1712- 1757), Colin McLaurin (1698-1746) o Gabriel Cramer (1704-1752)), estudiaron la razón por la cual las abejas realizan este diseño para la construcción de sus panales. Durante mucho tiempo se pensó que el motivo era que de esta forma aseguraba, en la línea de lo comentado anteriormente, que el prisma hexagonal terminado en tres rombos inclinados era la forma óptima para almacenar más volumen de miel por superficie de cera. Sin embargo, en 1965 el matemático húngaro Lászlo Fejes Tóth (1915-2005) descubrió que había otras formas de cerrar el prisma hexagonal que economizaban más la cera (la superficie), con dos hexágonos y dos pequeños rombos (como en un octaedro truncado). Aunque este diseño es tan solo un 0,035% más eficiente. Realmente no es una gran diferencia respecto al diseño natural de las abejas, aunque desde el punto de vista matemático tiene una gran relevancia. Establece que el diseño de las abejas no es “matemáticamente” el óptimo y deja abierto el problema de encontrar la mejor geometría del panal de abejas “ideal”.

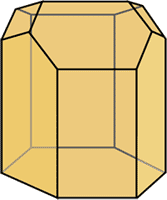
Volviendo al libro del autor de las tres leyes sobre el movimiento de los planetas alrededor del Sol, las leyes de Kepler, otra de las ventajas de la forma en que las abejas cierran las celdas por la parte del fondo es que esto permite a las abejas construir dos familias de celdas encajadas, perfectamente y sin dejar huecos, por la parte de atrás de las mismas, pero abiertas en sentido contrario unas de las otras.

Así, cada celda comparte una de sus paredes con 6 celdas adyacentes, y además las tres paredes rómbicas, con otras tantas celdas colocadas en el sentido contrario.

A raíz de la forma que tienen las terminaciones de las celdas de las abejas, Kepler se planteó la siguiente cuestión: ¿existirá un cuerpo, similar a los cinco poliedros sólidos regulares y a los catorce poliedros arquimedianos (*), que pueda ser construido nada más que por rombos? Kepler encontró dos de estos cuerpos, uno con 12 rombos, el rombododecaedro, y otro con 30 rombos, el triacontaedro rómbico (dual del icosidodecaedro).

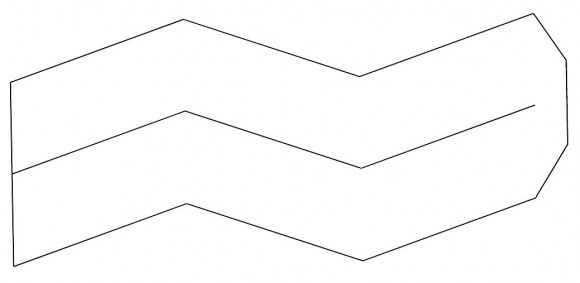
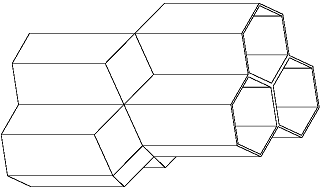
Pero más aún, el astrónomo y matemático alemán se percató de que el rombododecaedro, al igual que ocurre con el cubo, es un poliedro que llena el espacio. Los vértices de ángulos obtusos (donde se juntan 3 rombos) rellenan juntándose de cuatro en cuatro, mientras que en los vértices agudos (donde se juntan 4 rombos) se juntan de seis en seis, como se muestra en la imagen.

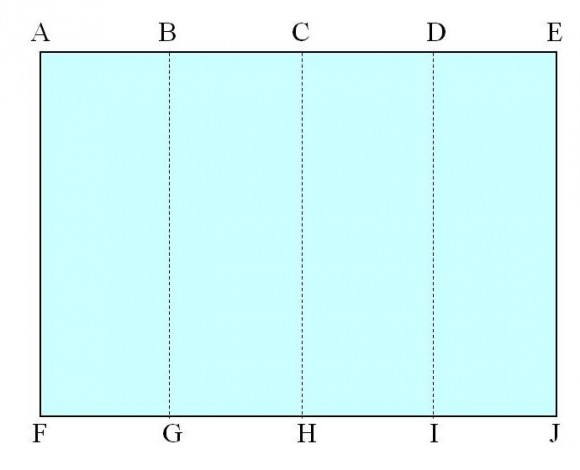
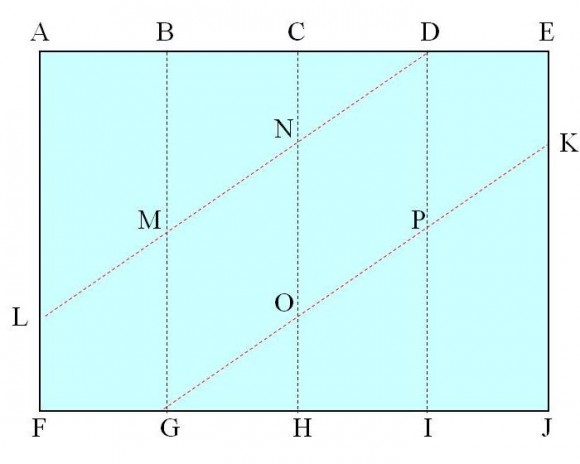
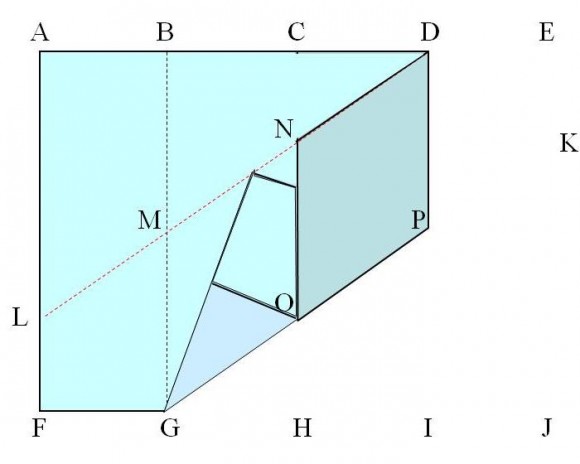
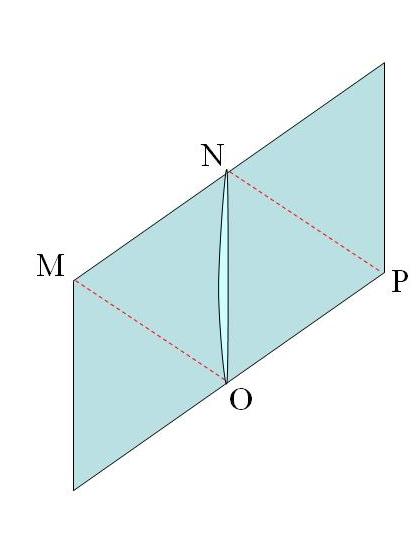
Pero la mejor manera de entender cómo es un poliedro, en este caso el rombododecadero, es construirlo físicamente y poderlo tocar con nuestras propias manos. Por este motivo, a continuación mostraré la construcción del rombododecaedro doblando papel. La idea es construir 12 módulos iguales, cada uno de ellos a partir de una hoja de papel de tamaño A5 (aunque podría ser A4 si queremos que sea más grande, o A6 para que sea más pequeño), que luego se ensamblarán dando lugar al poliedro.

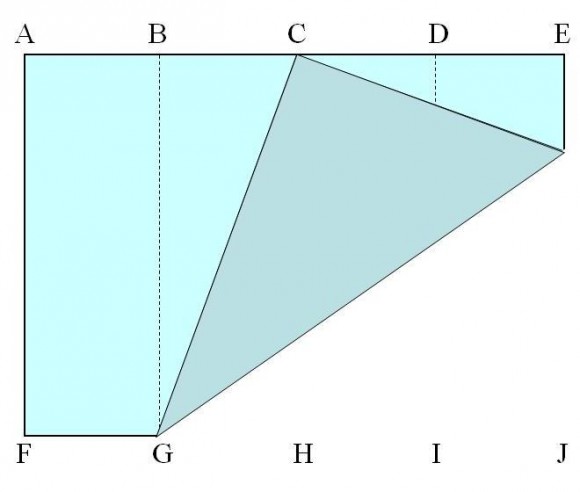
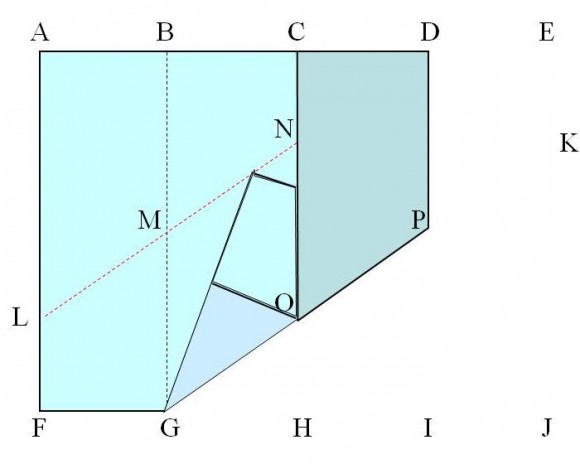
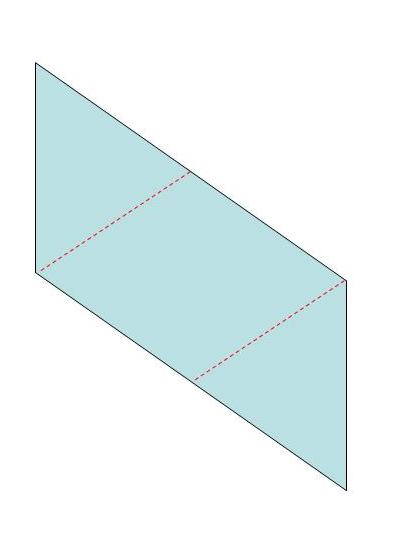
Este es un sencillo método de construcción del rombododecaedro que no necesita de más material que hojas de papel (de tamaño A5, las cuales se pueden obtener dividiendo hojas de tamaño A4 por la mitad) y doblarlas. No se necesitan ni tijeras ni pegamento, y a pesar de ello es una construcción bastante estable. Por este motivo, es un método muy interesante para organizar un taller para jóvenes. Además, al final del mismo se pueden poner juntos todos los rombododecaedros construidos y formar una gran teselación del espacio, es decir, una estructura que llena “todo el espacio”, sin dejar huecos.

Pero existen otros diseños para construir con papel un rombododecaedro, pero haciendo uso de las tijeras y el pegamento. Uno muy interesante que descubrí, mientras escribía esta entrada, en la página web PaperMatrix es el siguiente.

Para esta construcción se utiliza una pieza patrón formada por dos tiras, unidas con una pequeña lengüeta (existe también la versión de tres tiras) y que se van entrelazando hasta formar el poliedro, y que deja ese diseño bicolor de rombos en cada cara. Es un diseño atractivo, aunque ahora sí hay que utilizar tijeras y pegamento. Las reglas para la construcción del rombododecaedro las podéis encontrar en la página web de PaperMatrix.

En mi próxima entrada del Cuaderno de Cultura Científica terminaremos el camino iniciado en esta. Hablaremos del rombododecaedro estrellado y el puzzle asociado.

Bibliografía

1.- Página web del artista Carles Gomila
2.- Poliedro estrellado, Juegos de Ingenio nº 2, RBA coleccionables, 2004
3.- Johann Kepler, Strena seu de nive sexángula (Regalo de año nuevo Sobre el copo de nieve hexagonal), traducción de Ana García Azcárate y Ángel Requena Fraile, editorial Avinareta, 2011.
4.- Kepler’s Discovery, On the Six-Cornered Snowflake
5.- George Hart, Johannes Kepler’s polyhedra
6.- Edith Padrón, De cómo la geometría entrelaza ciencia y arte: Historia de un poliedro, Un paseo por la Geometría 2002/03, UPV-EHU, 2003.
7.- Arquimedes’s Laboratory, The geometry of the bees… (puzzle 117)
8.- PaperMatrix, Woven Rhombic Dodecahedron

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Esta entrada participa en la Edición 5.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.