
En mi entrada anterior del Cuaderno de Cultura Científica El rombododecaedro estrellado: arte, abejas y puzzles (primera parte) ya comenté que estos dos artículos sobre el rombododecaedro, su estelación -el rombododecaedro estrellado- y el puzzle que se basa en la descomposición en seis piezas iguales de este poliedro, estaban motivados por el cuadro Lady Kumiki de Carles Gomila (cuya web os recomiendo que visitéis). La anterior entrada (primera parte) la centramos en el rombododecaedro, los panales de las abejas, que están relacionados con este, y la construcción del mismo doblando papel.

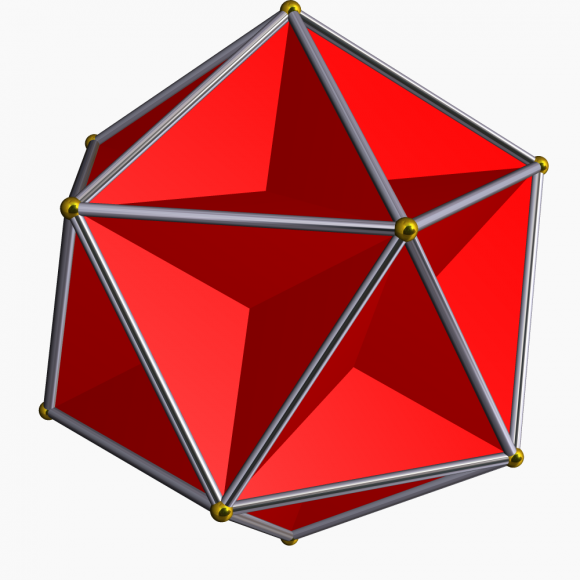
A partir de este poliedro convexo, el rombododecaedro, puede construirse un poliedro estrellado, el rombododecaedro estrellado, también conocido como sólido de Escher, debido a que es uno de los dos poliedros que aparecen en la famosa litografía Cascada (1961) del artista holandés M. C. Escher (1898-1972).

El proceso de estrellación para construir nuevos poliedros a partir de otros ya conocidos, como los sólidos platónicos o los arquimedianos, consiste en la extensión de las caras planas del poliedro hasta que se vuelven a intersecar para formar un nuevo poliedro. Con algunos poliedros este proceso no lleva a ninguna parte, como es el caso de la estrellación del tetraedro o del cubo, sin embargo, si consideramos un dodecaedro y extendemos sus lados se obtiene el pequeño dodecaedro estrellado (véase la imagen de más adelante).


En el proceso de estrellación de un poliedro (respectivamente, de un polígono) puede construirse más de un nuevo sólido (resp. polígono) estrellado. Una vez obtenida la primera estrellación se podrían seguir extendiendo las caras del poliedro (resp. los lados del polígono) con el fin de construir una segunda estrellación, o más si se continúa. Por ejemplo, existen tres estrellaciones del dodecaedro y veinte del icosaedro. O en el caso de los polígonos, el heptágono tiene dos estrellaciones (una obtusa y otra aguda) y el nonágono (polígono regular de 9 lados, también llamado eneágono regular) tiene tres.


Si ahora realizamos el proceso de estrellación a partir del rombododecaedro se obtendrá el poliedro que aparece en el cuadro Lady Kumiki de Carles Gomila, el sólido de Escher o rombododecaedro estrellado. Este sólido estrellado también se conoce con el nombre de primera estrellación del rombododecaedro, debido a que existen otras dos estrellaciones más (que pueden verse en la página Wolfram MathWorld), y la nuestra es la que primero aparece.
Como resultado de esta primera estrellación del rombododecaedro, sobre cada uno de los rombos que lo conforman aparece una pirámide (con base un rombo).
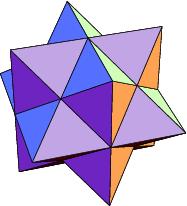
Este sólido estrellado satisface dos propiedades muy interesantes. La primera es que, al igual que el rombododecaedro, este también “tesela” el espacio, es decir, lo llena sin dejar huecos. Si disponemos de varias copias del rombododecaedro estrellado se pueden acoplar perfectamente unas con otras sin que queden espacios libres entre ellas.

La mejor manera de comprobar que el rombododecaedro estrellado llena el espacio, además de la puramente experimental que consistiría en coger varias copias del mismo y ver que efectivamente se pueden poner unas pegadas a las otras, es la siguiente.
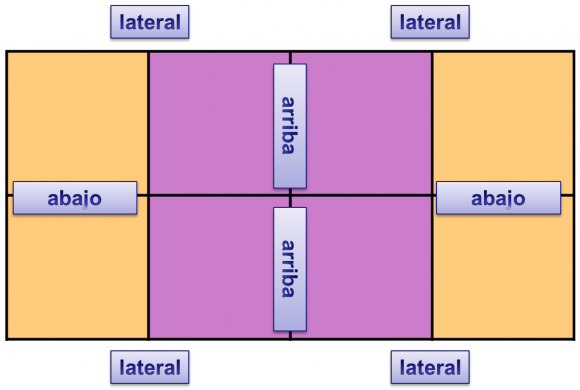
Observemos que este poliedro estrellado está inscrito (es decir, contenido) en un cubo, y que este cubo se puede dividir en ocho cubitos (si lo cortásemos por la mitad en las tres direcciones principales, secciones paralelas de las caras), cuatro arriba y cuatro abajo (lo cual podemos imaginarlo perfectamente al observar la imagen de abajo). Además, el rombododecaedro estrellado inscrito en el cubo también queda dividido en ocho partes, de tal forma que en cada cubito la parte del sólido de Escher se compone de tres pirámides (como se ve en la segunda imagen de abajo), y la parte del cubito que no está en el sólido de Escher se compone de otras tres pirámides iguales a las anteriores, que las complementa hasta formar el cubito. En consecuencia, en cada una de las ocho partes en que se divide el rombododecaedro estrellado se puede apoyar otro sólido de Escher para llenar el espacio. Por tanto, en cada uno de estos poliedros estrellados se apoyan otros ocho, al llenar el espacio.


Por lo tanto, estamos diciendo que el rombododecaedro estrellado podría construirse uniendo 3 x 8 = 24 pirámides. Y eso es exactamente lo que he hecho mientras escribía esta entrada del Cuaderno de Cultura Científica, construir un sólido de Escher mediante pirámides de papel.
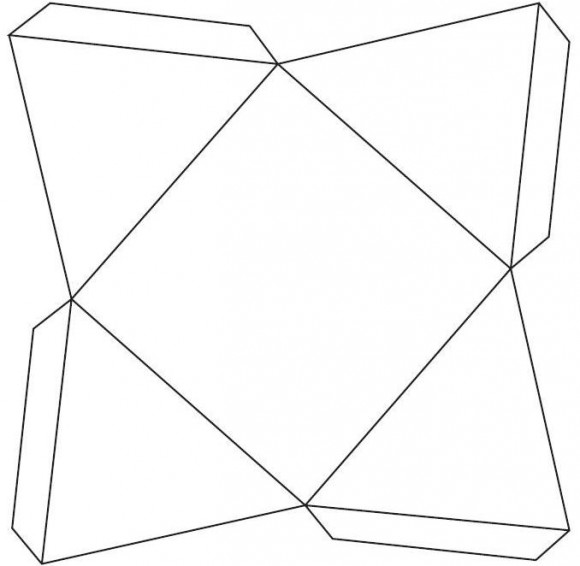
En primer lugar, sobre papeles de diferentes colores he impreso 24 copias del modelo de uno de los desarrollos planos de esta pirámide, con sus correspondientes pestañas laterales para que una vez cortada la plantilla y doblada por las aristas, poder pegar las caras, con la ayuda de las pestañas, y tener así construida nuestra pirámide. Aquí tenéis dos posibles despliegues planos de la pirámide (desarrollo 1 y desarrollo 2), por si queréis construir vosotros mismos el rombododecaedro estrellado.

Una vez realizadas las pirámides básicas, las fui pegando en grupos de tres, por las correspondientes caras y combinando los colores, para construir las 8 partes en las que se descompone este poliedro estrellado (como se muestra en la imagen).
A continuación, uní las cuatro piezas tripiramidales (formadas por tres pirámides cada una) de la parte de abajo y las cuatro piezas de la parte de arriba (como se ve en la siguiente imagen), para lo cual pegué las piezas por las correspondientes caras. Y finalmente había que unir las dos mitades para formar este colorido rombododecaedro estrellado.
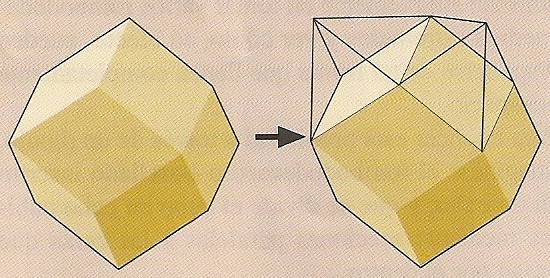
Por otra parte, si en lugar de pegar “de forma rígida” (como yo he hecho) las 8 piezas en las que se descompone el sólido de Escher, se unen dichas piezas por las aristas con cinta adhesiva (de una determinada manera), a modo de bisagras que nos permitan mover las piezas por esas uniones, entonces se construye lo que se conoce como el Cubo de Yoshimoto.
El cubo de Yoshimoto fue inventado en el año 1971 por Yoshimoto Naoki, al descubrir que las 8 piezas tripiramidales mencionadas anteriormente del rombododecaedro estrellado, podían ser unidas de tal manera que mostradas de una forma producían el poliedro estrellado, pero al colocarlas de otra se obtenía un cubo. Yoshimoto utilizó este cubo en 1972 en su exposición «From Cube to Space«. Además, en 1982 el “Cubo de Yoshimoto Nº. 1” fue incluido en la exposición permanente del MOMA (Museo de Arte Moderno), en cuya tienda se puede comprar la versión comercial.

En el siguiente video podéis observar las diferentes transformaciones del cubo de Yoshimoto.
Pero volvamos al rombododecaedro estrellado. Más arriba, habíamos comentado que este poliedro tenía dos propiedades interesantes, y una de ellas era su capacidad de llenar el espacio. La otra es que este sólido se puede dividir en 6 partes iguales (véase la imagen siguiente), las cuales constituyen un puzzle muy interesante. Uno que me encanta. Por lo tanto, el reto del puzzle consiste en unir estas seis piezas para montar el sólido de Escher.


Una de las dificultades de este puzzle es que montar las cinco primeras piezas no es muy complicado, lo más difícil es encajar la sexta pieza, lo cual se puede llegar a hacer con mucho cuidado y separando lo necesario las demás. Sin embargo, la solución más natural no sería esta, sino montar primero dos partes de tres piezas, de forma que encajasen después una con la otra, formando así el sólido de Escher. Pero no desvelemos la resolución, que cada uno lo intente en su casa…
Para aquellas personas que no tengan el puzzle, he encontrado una forma de construir las piezas con origami (diseño de Gadi Vishne), aunque no parece sencillo, podéis encontrar las instrucciones aquí.
Bibliografía
1.- Página web del artista Carles Gomila
2.- Stellation (Wikipedia)
4.- Página oficial de M. C. Escher
5.- Bruno Ernst, El espejo mágico de M. C. Escher, Taco, 1989.
6.- Poliedro estrellado, Juegos de Ingenio nº 2, RBA coleccionables, 2004
7. Livio Zefiro, The compound of three octahedra and a remarkable compound of three square dipyramids, the Escher’s solid
8.- Marta Macho, El cubo “mágico” de Naoki Yoshimoto, ZFTNews
9.- Yoshimoto Naoki, Yoshimoto Cube Nº. 1, MOMA (Museo de Arte Moderno)
10. Exploratorium, Exploring a complex space-filling shape
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica








Manuel
Hay otro tipo de estrellación muy interesante que consiste en prolongar las aristas del poliedro en cuestión hasta que por intersecciones sucesivas determinen el nuevo poliedro estrellado. Son ejemplos muy conocidos el pequeño dodecaedro estrellado y el gran dodecaedro estrellado; el primero obtenido prolongando las aristas de un dodecaedro regular y el segundo haciendo lo propio con las aristas del icosaedro. Es evidente que el primer caso se obtiene, indistintamente, prolongando las aristas como las caras del dodecaedro, pero el segundo no es una estrellación del icosaedro. En otros casos como en las estrellaciones de los Arquimedianos el procedimiento de las aristas sí es correcto y a veces el único posible. Por ejemplo, el hexaedro truncado estrellado (Stellated Truncated Hexahedron), el pequeño dodecaedro truncado estrellado (Small Stellated Truncated Dodecahedron) o el gran dodecaedro truncado estrellado (Great Stellated Truncated Dodecahedron). Por cierto las estrellaciones del icosaedro son cincuenta y nueve, no veinte como dices en tu artículo.
Muy interesante y muchísima paciencia la construcción en cartulina de esas pirámides de base rómbica que indicas en tu escrito. Para los lectores interesados les indico que poniendo 12 pirámides con las puntas hacia dentro sale (como bien dices) el rombododecaedro, si añades otras 12 pegadas en las caras de dicha figura pero ahora con las puntas hacia afuera obtienes la primera estrellación (Escher). Si ahora en los huecos que deja la figura anterior pones, con las puntas hacia dentro, otras 24 pirámides, se obtiene la segunda estrellación y si, finalmente, rellenas los huecos con los picos hacia dentro de forma alternada tienes la tercera (¡y última!) estrellación del rombododecaedro. En total 72 pirámides ¡buen puzzle!
En la primera parte de tu Artículo te hice un comentario, que supongo no has tenido tiempo de revisar, en el que aparte de otras cuestiones indicaba la manera más eficiente de comprender la estructura de la celda de Fejes Tóth.
Felicitaciones por tu página y hasta pronto
Catalina Araceli García Rosas
Interesante actividad espero puedan tener el desarrollo plano del puzzle
Manuel
Para Catalina Araceli
El desarrollo plano de la pirámide fundamental que yo indico en mi comentario, con la que se construye el rombododecaedro y sus tres estrellaciones, a modo de puzle muy divertido e instructivo, es distinta de la descrita por Raúl y que incluye un dibujo en su artículo.
La pirámide a la que yo me refiero es de fácil construcción y se procede así: la base es un rombo que tiene sus diagonales en relación raíz cuadrada de dos, las caras laterales son cuatro triángulos isósceles iguales que, si se toma un lado como unidad, los otros dos valen un medio de raíz cuadrada de tres. Como resulta que este último valor es el lado del rombo que actúa de base, habrá que disponer los triángulos laterales de forma que exista concordancia entre las longitudes respectivas. Una vez pegadas todas las partes, se obtiene la pirámide recta de base rómbica comentada más arriba, de la que se deben hacer 72 réplicas para lograr el puzle secuencial aditivo. Pido disculpas por no incluir un dibujo de la plantilla, pero creo que no tiene pérdida por su sencillez.
Si eres aficionada a construir cuerpos por pegado de sus desarrollos planos, tal vez te interese la figura que propongo en el enlace http://gaussianos.com/pappus-hales-y…-eficiente/
Saludos afectuosos
Manuel