Hoy me vais a permitir que os ofrezca una entrada diferente a las que he escrito hasta ahora. Se trata más bien de lo que podríamos llamar una entrada-exposición, pero sin “audio-guía”. Esta entrada-exposición está compuesta por algunas obras de un artista para quien las matemáticas son fundamentales en su trabajo, es el artista francés Bernar Venet (nacido en 1941).

Bernar Venet es un artista conceptual que utiliza las matemáticas como un elemento central en su obra. Ángulos, líneas, circunferencias y otras formas geométricas, diagramas matemáticos, fórmulas matemáticas, artículos de investigación y textos matemáticos, forman parte de sus esculturas, pinturas y fotografías.

Hoy me gustaría centrarme en una serie de obras inspiradas en la estética de las fórmulas y textos matemáticos. Estas obras son abstractas, aunque desde una perspectiva diferente a lo que conocemos como pintura abstracta, pero al mismo tiempo muy interesante. Para las personas que no pertenecen al ámbito matemático, o científico, los símbolos, términos y fórmulas matemáticas que aparecen representadas no tienen ningún significado más que el puramente estético, o quizás también un cierto significado simbólico o metafórico. Al contemplar estas obras se puede apreciar una cierta armonía, más aún, una cierta belleza, fruto de la relación estética de los elementos que la componen, pero la mayoría de las personas son incapaces de reconocer los elementos matemáticos de la misma y sus significados.

Por otra parte, las matemáticas son un lenguaje universal, que pueden entender personas de todas las partes del mundo, con independencia de cuál sea su lengua hablada y escrita. Todas las personas del mundo entienden el significado de la expresión matemática, 2 + 2 =4, por lo que paradójicamente estas obras también hablan de un lenguaje común a lo largo de todo el planeta.

Una de las técnicas utilizadas por Bernar Venet es ampliar a un tamaño grande estas imágenes de fórmulas y textos matemáticos, lo que resalta aún más su fuerza estética.

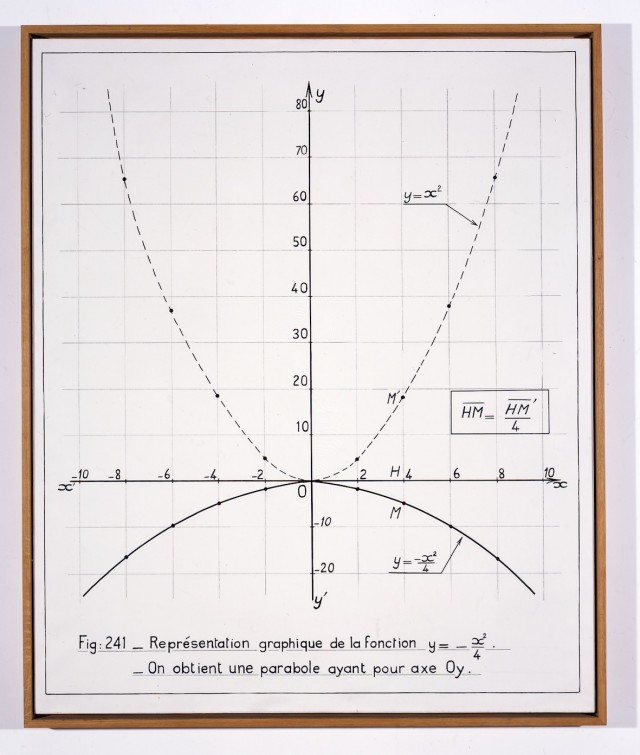
En su viaje a Nueva York en 1966, Bernar Venet tras haberse relacionado previamente con movimientos artísticos como el action painting (una de las ramas del expresionismo abstracto), el nuevo realismo o el arte pop, se vería influenciado por el minimalismo. Es en esa época cuando empieza a interesarse por las matemáticas y la lógica, que empieza a incorporar en sus obras. De ese año son obras como las siguientes, en las que representa diagramas matemáticos que aparecen en textos científicos (matemáticas, física, ingeniería, etc): Vectores iguales, vectores opuestos (tinta y acrílico sobre lienzo, 1966), Proporción de dos cantidades (acrílico sobre lienzo, 59 x 48 cm, 1966), Representación gráfica de la función y = – x²/4 (acrílico sobre lienzo, 146 x 121 cm, 1966) o Parábola de la función y = 2 x² + 3 x – 2 (acrílico sobre lienzo, 168 x 97 cm, 1966.

En los años siguientes realizó una serie de obras que recogían diferentes partes de artículos y libros científicos, en particular, relacionados con las matemáticas. Algunas de estas obras: Generando números pseudo-aleatorios “mezclando” una sucesión de Fibonacci (ampliación fotográfica, 1967), Nota sobre permutaciones aleatorias (ampliación fotográfica, 1968) Teoría de conjuntos: unión e intersección de familias de conjuntos (4 ampliaciones fotográficas, 175 x 115 cm, 1969) o Teoría elemental de números (ampliación fotográfica y libro, 1970).

En otro grupo de obras, que el artista francés, pero que reside en EE.UU., denomina “wall paintings” (o pinturas murales), está dedicada a una única fórmula o diagrama matemático que ha obtenido de artículos y textos matemáticos, y que pinta sobre una gran pared. A esta serie pertenecen obras como: Related to: The homology sequence of a Triple as exact (acrílico sobre pared, 2000), Related to: The visualisation of the covariant volume integral (acrílico sobre pared, 2000), The S Matrix element (acrílico sobre lona, 2001), Related to: The Homology (Cohomology) Sequence of a Pair (X,A), (acrílico sobre pared, 2001), A parametric ordinary differential equation of the first order in two dimensions (acrílico sobre pared, 2001).

Una serie relacionada con la anterior es la serie “equation paintings” (o pinturas de ecuaciones), en la que de nuevo toma fórmulas y diagramas matemáticos de artículos y libros y los representa sobre lienzo. Ambas series se diferencian simplemente en el formato, es decir, realizadas en grandes tamaños sobre una pared en la anterior serie, y en lienzos grandes, pero más pequeños, en esta. Entre las obras que pertenecen a esta serie tenemos: Related to: Sampling from a Normal Population (acrílico sobre lienzo, 195 x 275 cm, 2000), Zig-zag path Zuv between notes u and v of neighborhood Bu in a planar mesh (acrílico sobre lienzo, 195 x 195 cm, 2000), Related to: Conmutative operation (acrílico sobre lienzo, 193 x 229 cm, 2001), Related to: Affine and Convex Sets and Functionals, (acrílico sobre lienzo, 210 x 170 cm, 2001), Three-Dimensional Faces and Quotients of Polytopes (acrílico sobre lienzo, 195 x 195 cm, 2001).

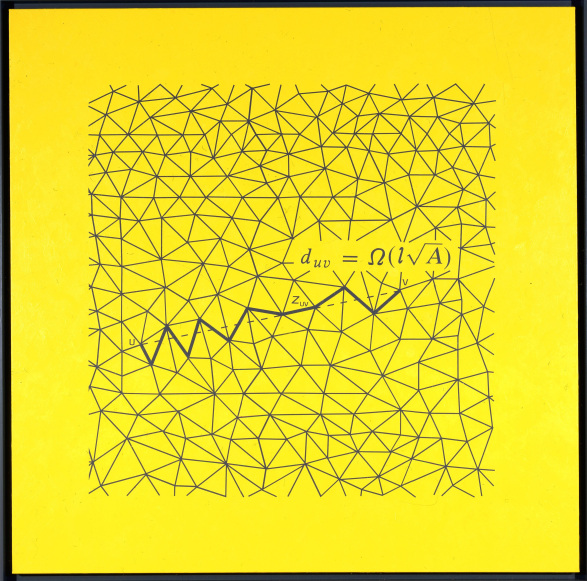
En el blog sobre combinatoria del matemático de la Universidad Hebrea de Jerusalem, Gil Kalai, este nos muestra como la imagen de esta última obra se ha basado en parte de la demostración principal del artículo Three Theorems, with Computer-Aided Proofs, on Three-Dimensional Faces and Quotients of Polytopes. En concreto es la página siguiente:

Otra serie de obras que incluyen fórmulas y expresiones matemáticas, así como parte de los textos de libros y artículos, pero superponiendo diferentes imágenes, es la serie “saturation paintings” (o pinturas de saturación). Algunas de las obras de esta serie son: Saturación 1 (acrílico sobre lienzo, 200 x 200 cm, 2002), Saturación con 33 ceros (acrílico sobre lienzo, 204 x 204 cm, 2006), Saturación con once puntos verticales a la derecha (acrílico sobre lienzo, 204 x 204 cm, 2006), Saturación con 2 y 3 (acrílico sobre lienzo, 204 x 204 cm, 2007), Saturación con dos veces “pour tout” (acrílico sobre lienzo, 204 x 204 cm, 2008), Saturación de color rojo con NN (acrílico sobre lienzo, 85 x 85 cm, 2008), Saturación (acrílico sobre lienzo, 204 x 204 cm, 2010).

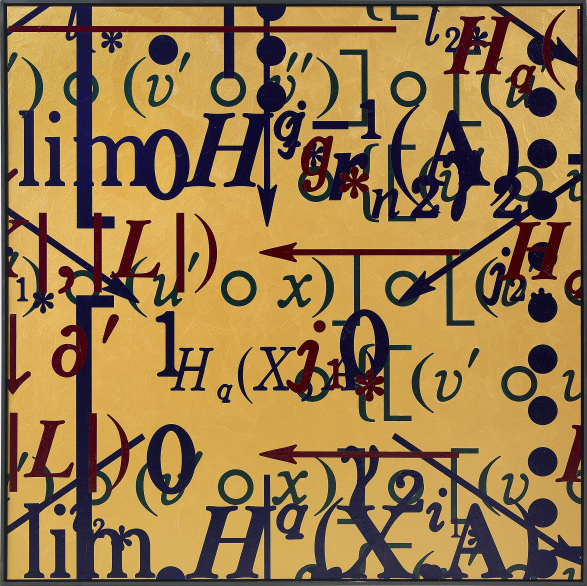
La última serie que vamos a mencionar hoy de las pinturas de Bernar Venet con fórmulas y expresiones matemáticas es la serie “shaped canvases” (o lienzos con formas), en la cual se trabajan las mismas ideas anteriores, pero realizadas sobre lienzos con diferentes formas geométricas. Algunas obras de esta serie son: Tríptico dorado con dos saturaciones (acrílico sobre lienzo, 247 x 593 cm, 2009), Doble saturación dorada con “of the circular arc” (acrílico sobre lienzo, 214 x 433 cm, 2010), Saturación dorada con “we determine finetely” (acrílico sobre lienzo, diámetro 247 cm, 2009), Rojo y dorado con “member function” (acrílico sobre lienzo, 181 x 212 cm, 2009), Pintura circular de oro, a Gödel (acrílico sobre lienzo, diámetro 212 cm, 2010), Homage to Al-Khawarizmi n°5 (acrílico sobre lienzo, 270 x 276 cm, 2013).

Pero antes de terminar con una de las obras más representativas y conocidas de esta serie, el Tríptico dorado con dos saturaciones, mostremos una imagen de su taller, del año 2002, con algunas de sus obras.

Bibliografía

1.- Página web de Bernar Venet

2.- Thomas McEvilley, Bernar Venet, Artha/Benteli, 2002.

3.- Barbara Rose, Bernar Venet, la paradoja de la coherencia, Generalitat Valenciana-IVAM, 2010.

4.- Images des Mathematiques, Bernar Venet, de l’art et des mathématiques

5.- G. Meisinger, P. Kleinschmidt, G. Kalai, Three Theorems, with Computer-Aided Proofs, on Three-Dimensional Faces and Quotients of Polytopes, Discrete Comput. Geom. 24, p. 413–420, 2000.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Nota: Esta entrada participa en la Edición 7.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.