Uno de los problemas clásicos de la matemática recreativa que aparece recogido en muchas de las publicaciones dedicadas a juegos y problemas de ingenio (por ejemplo, clásicos de la matemática recreativa como Recreaciones Matemáticas (1891) de E. Lucas; Mathematical Recreations and Essays (1892), de R. Ball; o Amusements in Mathematics (1915), de H. E. Dudeney), es el conocido como Problema de las colegialas de Kirkman, que podríamos enunciar de la siguiente forma:

Problema: Quince jóvenes estudiantes salen de paseo todos los días de la semana, de lunes a domingo, de forma ordenada, formando cinco filas de tres estudiantes cada una, ¿cómo organizarlas todos los días de la semana para que ningún par de alumnas compartan fila más de un día?

Este problema fue propuesto originalmente por el reverendo y matemático británico Thomas P. Kirkman (1806-1895). Aunque se suele citar como publicación original de este problema la revista de matemática recreativa The Lady’s and Gentleman’s Diary de 1850, lo cierto es que el experto en teoría de grupos y combinatoria Thomas P. Kirkman lo publicó en 1847 en Cambridge and Dublin Mathematical Journal.

La primera solución a este problema fue dada por el matemático británico Arthur Cayley (1821-1895) en un artículo publicado en 1850 en la revista Philosophical Magazine, «On the triadic arrangements of seven and fifteen things». Ese mismo año, Kirkman publica su solución en Cambridge and Dublin Mathematical Journal, con el título «Note on an unanswered prize question». El matemático británico James Joseph Sylvester (1814-1897) también investigó sobre esta cuestión y afirmó que Kirkman le había robado la idea.

Pero volvamos al problema planteado por Thomas P. Kirkman. Se puede considerar la cuestión para un número n cualquiera de jóvenes estudiantes, de hecho este es un caso particular de lo que se conoce en combinatoria como “sistemas triples de Steiner”, que no vamos a considerar en esta entrada y que quizás debieron de llamarse “sistemas triples de Kirkman”.

Si consideramos el problema general en el que pasean n estudiantes, el número de posibles parejas de jóvenes que se pueden formar dentro de ese grupo de n es 1/2 n (n – 1), el número de días que se requieren para realizar todos los paseos es 1/2 (n – 1), que es igual a la cantidad de grupos de tres en los que está una colegiala cualquiera, y por supuesto, el número de jóvenes tiene que ser múltiplo de 3. Por lo tanto, la sucesión de posibles valores para el número n de jóvenes estudiantes para las que quizás se pueda diseñar una serie de paseos como los planteados en el problema es 3, 9, 15, 21, etc, es decir, aquellos que son de la forma 6 m + 3, o matemáticamente, congruentes con 3 módulo 6.

Existen muchos métodos para generar soluciones al problema de las colegialas de Kirkman, en particular, para el caso clásico de n = 15, aunque en esta entrada solamente vamos a mostrar dos, uno geométrico y otro utilizando un sencillo argumento de combinatoria.

Para el caso más sencillo, n = 3, de solo tres estudiantes, la solución existe y es trivial. Un único día las tres estudiantes van a pasear juntas, formando el único grupo de tres estudiantes posible.

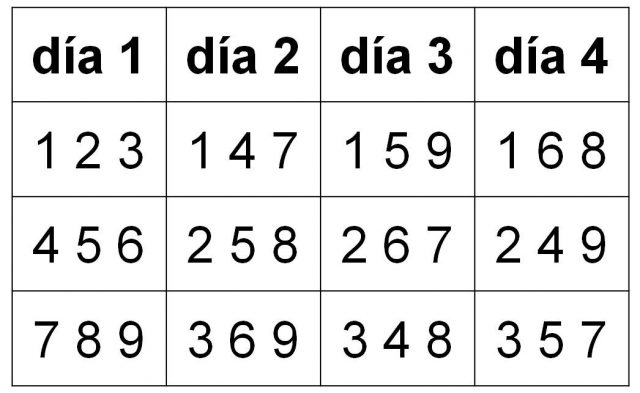
Para n = 9 jóvenes estudiantes, el número de días que se requieren para realizar los paseos son 4 y existe una única solución. Con un poco de orden, se puede obtener fácilmente la solución. Si denotamos a cada estudiante por un número del 1 al 9, esta es:

En el libro Las últimas recreaciones: huevos, nudos y otras mistificaciones, Martin Gardner muestra un diseño geométrico que proporciona la solución para n = 9, y que nos ayuda a comprender el diseño geométrico para n = 15 que mostraremos más adelante. Se dibuja un círculo y en él se colocan ocho signos, distribuidos con el mismo espacio entre ellos, y otro signo en el centro, por ejemplo, las nueve primeras letras A, B, C, D, E, F, G, H, I, que se corresponden con las 9 estudiantes. Por encima de este círculo dibujaríamos otro círculo concéntrico, del mismo diámetro, sobre el que se marcan tres grupos de tres letras (dos triángulos y una recta), como se muestra en la imagen.

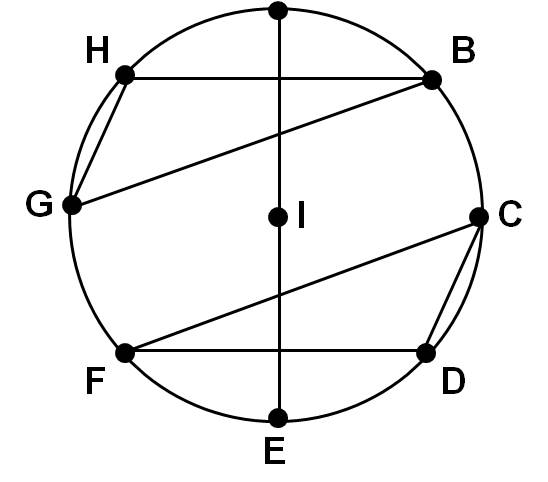
En este diagrama se describen los tres tríos de estudiantes –es decir, las tres filas- de la primera jornada, AIE / HBG / CFD, y rotando una posición cada vez el segundo disco, con los dos triángulos y la recta, se obtienen los grupos de tres de las siguientes jornadas. Esta solución es obviamente la misma que la anterior, para lo cual solo hay que observar la relación entre letras y números (A = 1, I = 2, E = 3, H = 4, B = 5, G = 6, C = 7, F = 8, D = 9).

Una solución geométrica al problema de las 15 colegialas de Kirkman se muestra también en el mencionado libro de Martin Gardner, Las últimas recreaciones: huevos, nudos y otras mistificaciones, que hace uso de nuevo de discos concéntricos que rotan.

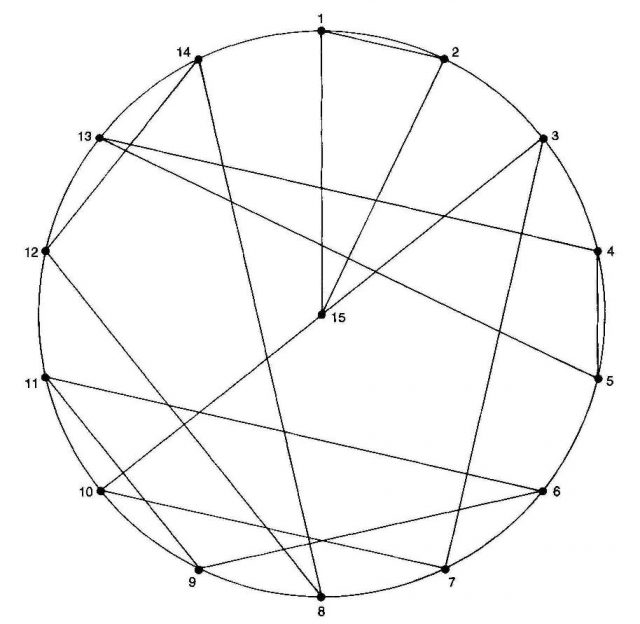
En la imagen se obtienen los grupos de tres estudiantes de la primera jornada, y para obtener los de las siguientes jornadas se rota, dos posiciones cada vez, el disco con los triángulos, obteniéndose así una solución completa del problema clásico de Thomas P. Kirkman:

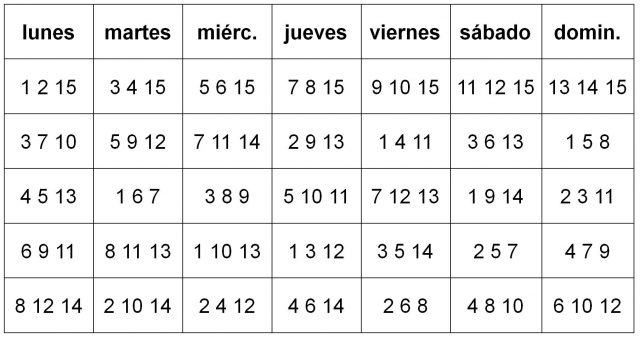
El método que vamos a mostrar a continuación para encontrar una solución al problema original de las colegialas de Kirkman, es decir, en el que pasean las 15 jóvenes estudiantes, es el que el reverendo Andrew H. Frost publicó en 1870 en la revista Quarterly Journal of Pure and Applied Mathematics, “General Solution and Extension of the Problem of the 15 Schoolgirls”, y que nos muestra Édouard Lucas en su libro Recreaciones Matemáticas (1891). Este es un método menos impactante que el método geométrico mostrado por Gardner, pero es un método que se puede obtener con un poco de lógica.

Si nos fijamos en una joven estudiante cualquiera, a la que designamos mediante la letra X, cada día va a encontrarse con dos de sus compañeras, en los siete paseos. Vamos a designar mediante una letra, de la A a la G, las estudiantes que están con X cada uno de los 7 días, añadiéndoles un subíndice para diferenciar entre las dos. Así, el lunes estará con A₁ y A₂, el martes con B₁ y B₂, etcétera. Luego los 7 grupos en los que aparece la estudiante X son

Como las estudiantes con la misma letra no se van a volver a encontrar en ningún paseo más, por ahora denotaremos a cualquiera de ellas solo con la letra, pero sin el subíndice, así representaremos a A₁ y A₂ con la letra A, a B₁ y B₂ con la letra B, etcétera. Y entonces, los grupos de tres estudiantes de las demás jornadas van a venir formados por grupos de tres letras de entre las siete posibles A, B, C, D, E, F, G, que en cada caso tendrán un subíndice u otro según corresponda.

Con estas siete letras se pueden formar siete tríadas fundamentales, es decir, grupos de tres letras de forma que dos de esas letras no se junten más de una vez (puesto que esta es la condición del problema de las colegialas):

Si miramos a estas siete tríadas, vemos que hay cuatro que no contienen a la letra A, por lo que son los grupos de tres estudiantes básicos (independientemente del subíndice) que irán en la columna del lunes, cuatro que no contienen a la letra B, que irán en la columna del martes, y así con el resto, obteniéndose la estructura básica de las filas siguientes, en las que no está X. Por lo tanto, en general, tenemos:

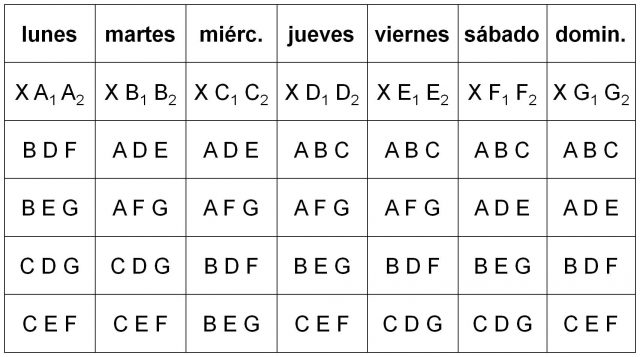
Llegados a este punto se trata de ver para cada triada fundamental, por ejemplo, B D F, que da lugar a cuatro combinaciones de las catorce muchachas tomadas de tres en tres que van a pasear (tengamos en cuenta que no se pueden repetir parejas y que los índices 1 y 2 se podrían escribir de otras maneras, pero se ha elegido la más sencilla), por ejemplo,

cómo pueden incorporarse en la tabla anterior de los paseos. Por lo tanto, se colocan estas cuatro combinaciones en la tabla de paseos de la semana, e incluso se completan algunos índices que quedan fijados al colocar estas. Y por lo tanto, quedaría así:

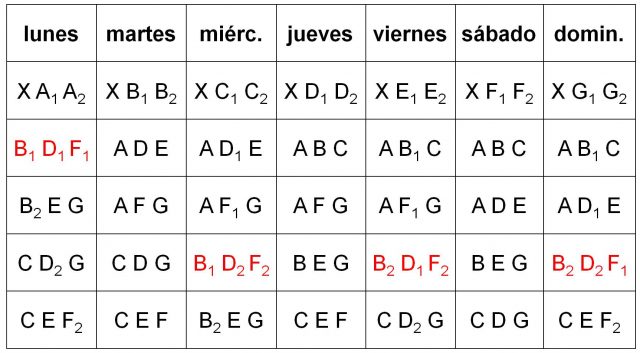
Ahora tomaríamos la siguiente tríada fundamental, por ejemplo, B E G, que es la siguiente fila del lunes, y que aparece con el índice 2 en la B tanto el lunes como el miércoles. De nuevo, se le asocian los índices para formar cuatro combinaciones:

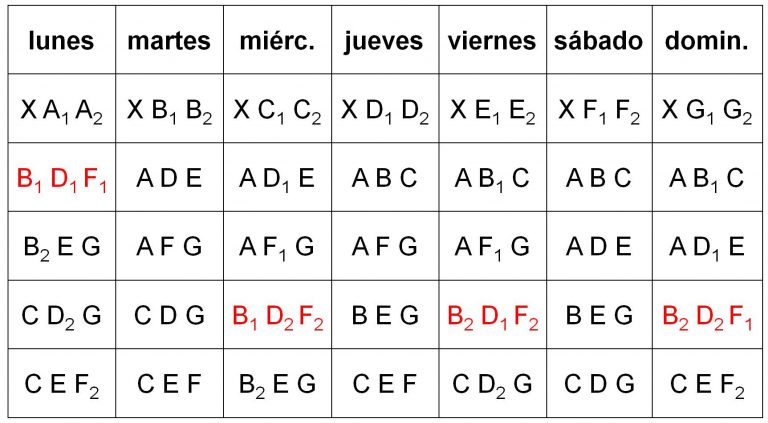
Y se colocan, como anteriormente, en el cuadro de los siete paseos. Después se continúa con el siguiente grupo fundamental de tres letras, C D G, y después con el resto de tríadas fundamentales, C E F, A D E, A F G y A B C, hasta obtener la tabla definitiva:

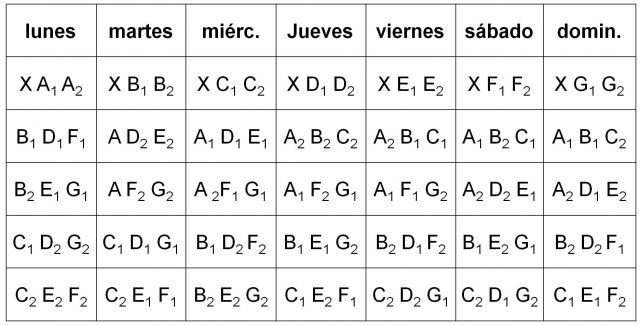
Desde el año 1922 se conoce que existen 80 soluciones al problema original de las colegialas de Kirkman, aunque de todas ellas solamente hay 7 que son soluciones básicas.

Por otra parte, como hemos comentado más arriba, para que exista solución al problema de Kirkman para n jóvenes estudiantes, este número debe tener la forma n = 6 m + 3, sin embargo, nada nos dice a priori que esta solución sea suficiente, que exista alguna solución. Poco a poco se fueron obteniendo algunas soluciones particulares para algunos valores concretos de n de esta forma, pero no fue hasta 1970 que los matemáticos D. K. Ray-Chaudhuri y Richard M. Wilson, de la Universidad de Ohio, demostraron que la condición era suficiente, es decir, que existen soluciones para todos los n de la forma 6 m + 3. Sin embargo, lo que se desconoce es el número de soluciones.

Bibliografía

1.- Miodrag S. Petkovic, Famous puzzles of Great Mathematicians, AMS, 2009.

2.- Martin Gardner, Las últimas recreaciones: huevos, nudos y otras mistificaciones, Gedisa, 2002.

3.- Édouard Lucas, Recreaciones Matemáticas, vol. 2, Nivola, 2007.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica