Siguiendo con la serie de entradas dedicadas al dinero que he iniciado en la sección Matemoción del Cuaderno de Cultura Científica con los artículos
hoy vamos a adentrarnos en un problema matemático clásico relacionado con el dinero, el conocido como Problema del cambio de moneda (de Frobenius).

Este problema, en su versión general, podría formularse de la siguiente forma:
Sea
un conjunto de números enteros positivos, relativamente primos (es decir, sin divisores comunes), ¿cuál es el entero positivo N más grande que no puede ser representado como combinación lineal de ellos, es decir,
, para
enteros positivos?
A este número se le suele denotar por y se le llama número de Frobenius.
El problema anterior se denomina “problema del cambio de moneda” porque se puede formular de la siguiente forma. Si en un país tienen monedas, o billetes, con valores de unidades de moneda (por ejemplo, supongamos que hubiese monedas de 4, 7 y 11 céntimos), el problema del cambio de moneda consiste en averiguar cuál es la mayor cantidad de dinero que no puede obtenerse, con estas monedas, o dicho de otra forma, cuál sería el valor más grande de un billete, de forma que no pudiese cambiarse utilizando monedas de esas cantidades (por ejemplo, si hay monedas de 4, 7 y 11 céntimos, ¿es posible que nos puedan cambiar un billete, o moneda, de 17 céntimos?, ¿y de 50 céntimos?).

El matemático alemán Ferdinand G. Frobenius (1849-1917) propuso, y discutió, este problema en algunas de sus conferencias, aunque nunca llegó a publicarlo.
El problema del cambio de moneda es trivial si tenemos solo un tipo de monedas, es decir, , ya que si
todo número natural puede expresarse como múltiplo de 1, pero si
es distinto de 1, existen infinitos números, cantidades, que no pueden ser obtenidas con esa única moneda.
La solución del problema para dos tipos distintos de moneda, es decir, , fue resuelto en 1884 por el matemático inglés James J. Sylvester (1814-1897).
Pero antes de resolverlo para cualesquiera valores , vamos a analizar un caso particular que nos ayude a entender un poco mejor la cuestión, el caso de las monedas con un valor de 4 y 7 unidades monetarias. Más aún, vamos a reformular el problema y plantearlo como un asunto de sellos, que es la otra forma en la que se suele mostrar el mismo (y que se denomina “problema de los sellos de Sylvester”).

Problema de los sellos de Sylvester: imaginemos una oficina de correos que en cierto momento solo dispone de sellos de 4 y 7 céntimos, ¿cuál es la cantidad más grande que NO puede ser puesta en un sobre utilizando solo esos dos tipos de sellos?
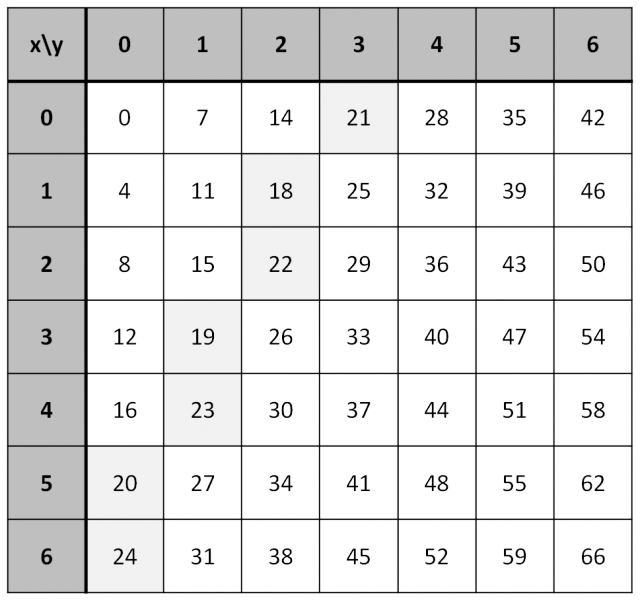
Las cantidades que SÍ pueden ser expresadas utilizando sellos de 4 y 7 unidades, son aquellas que podemos expresar de la forma
, para
.
Veamos en la siguiente tabla las cantidades que SÍ pueden ser obtenidas, en función de los valores de e
(números enteros no negativos).
Si nos fijamos en la tabla anterior, los números que no pueden ser representados de la forma , es decir, las cantidades que no se pueden representar en el sobre con sellos de 4 y 7 unidades, son
1, 2, 3, 5, 6, 9, 10, 13 y 17,
y las cantidades más grandes que 17 sí pueden ser representadas. Por ejemplo, , la cantidad 37 se puede obtener con 4 sellos de 4 unidades y 3 sellos de 7 unidades. Por lo tanto, la solución al problema de Frobenius para
, o al problema de los dos sellos de correos con valores de 4 y 7 unidades, es
.
La solución general al problema de los sellos de Sylvester, es decir, el cálculo del número de Frobenius, está dada por la siguiente fórmula
Más aún, las cantidades que no se pueden representar como suma de múltiplos, no negativos, de a y b, es igual a la mitad de los números que hay entre 1 y , es decir, hay
números que no pueden ser representados. Si nos fijamos en el caso particular de 4 y 7, tenemos que y hay 9 cantidades que no pueden ser representadas con esos dos tipos de sellos.
En la siguiente tabla podemos observar cuáles son esos números a partir de los cuales todas las cantidades pueden ser representadas en función de los dos valores de los sellos, los números de Frobenius.
Volviendo a la solución del problema del cambio de moneda de Frobenius para , o el problema de los sellos de Sylvester, la ecuación que hay que resolver
,
es lo que se conoce como una ecuación diofántica lineal. A continuación, vamos a mostrar algunas ideas relacionadas con su resolución matemática.
Paso 1 (La identidad de Bezout). Dados dos números enteros positivos a y b, cuyo máximo común divisor es d, entonces existen dos números enteros x e y, tales que
Esta identidad es una consecuencia inmediata del algoritmo de divisibilidad de Euclides.
En el caso particular, en el que a y b no tengan divisores comunes, que es el caso que hemos planteado aquí, entonces existen dos números enteros x e y, tales que
Paso 2 (La ecuación diofántica lineal). Como consecuencia de la identidad de Bezout, dados dos números enteros positivos a y b sin divisores comunes, entonces cualquier número entero z puede expresarse como combinación lineal de a y b, es decir, existe solución a la ecuación diofántica lineal . En general, existen muchas soluciones enteras (es decir, que x e y pueden tomar también valores negativos) a la anterior ecuación. Por ejemplo, si tenemos una solución x e y, también son soluciones
, y
.
En el ejemplo anterior, .
Paso 3 (Solución del problema de los sellos de Sylvester). Dados dos números sin divisores comunes a y b (que son los valores de los sellos), y una cantidad positiva k (que es la cantidad que nosotros queremos obtener con los sellos), la solución a la cuestión de si podemos obtener esa cantidad con esos dos tipos de sellos, es equivalente a si la ecuación diofántica lineal tiene solución, con x e y no negativos.
Hemos visto que existen muchas soluciones (de hecho, hay infinitas) a la ecuación diofántica lineal, en las cuales x o y pueden ser negativos. Pero en el problema de Sylvester nosotros estamos interesados en soluciones positivas de x e y. Puede verse que la única manera de que la ecuación tenga solución con números no negativos es que si fijamos que , el número y de la solución correspondiente cumpla que
.
Por lo tanto, como el problema de Sylvester nos pregunta cuál es la mayor cantidad para la que esto no ocurre, el número más grande para el que no ocurre eso es para cuando
e
, luego
Existen muchas demostraciones de este hecho, y también, del cálculo del número de cantidades que no se pueden obtener como combinación lineal de los dos tipos de sellos. Para quienes estén interesados en profundizar más en el tema y en las demostraciones matemáticas, algunas referencias interesantes y asequibles son [2, 3].
La siguiente entrada del cuaderno la dedicaremos al problema del cambio de moneda de Frobenius, cuando se disponen de tres, o más, tipos de monedas, y al problema de los nuggets de pollo, que está relacionado con el anterior.
Pero, para terminar esta entrada, vamos a mencionar brevemente un tema relacionado con el problema de los sellos de Sylvester, que son los ciclos vitales de Fliess.
En la entrada del Cuaderno de Cultura Científica titulada El enigma del número 23, dedicamos la última parte a los biorritmos o ciclos vitales del médico alemán Wilhelm Fliess (1858-1928).
Recordemos en qué consistían estos. Según la teoría de Fliess, la vida de las personas, y el mundo en general, está gobernado por dos ciclos vitales, uno el femenino (28 días) y otro el masculino (23 días). La ecuación vital de cada persona está determinada por lo que aporta la parte masculina y la femenina a la persona.
Trabajando numéricamente con estos dos ciclos, 23 y 28, es decir, combinando los múltiplos de ambos números, consiguió imponer un modelo numérico de casi todo, que introdujo en su obra Las relaciones entre la nariz y los órganos sexuales femeninos desde el punto de vista biológico (1906).
Un ejemplo de su método, de los muchos que aparecen en su obra de 1906, es el siguiente. “Durante 4 días del año 1815, concretamente los días 19 y 25 de agosto, así como los días 15 y 19 de octubre, Schubert compuso una increíble cantidad de sus mejores obras. Los intervalos entre estos días dan lugar a lo siguiente: del 19 de agosto al 19 de octubre = 61 días = 2 veces 28 más (28 menos 23), así como del 25 de agosto al 15 de octubre = 51 días = 2 veces 28 menos (28 menos 23)”. Es decir, y
.
Fliess era amigo íntimo del padre del psicoanálisis Sigmund Freud (1856-1939), quien inicialmente pensaba que la teoría de Fliess era una de las mayores revoluciones en biología. Freud pensaba que el placer sexual estaba relacionado con un ciclo de energía de 23 días y la insatisfacción con uno de 28 días, creía que moriría a los 51(= 23 + 28) años, edad crítica y recogió algunas de las ideas de Fliess en su libro “La interpretación de los Sueños”. Así escribe en este libro que “cincuenta y uno es una edad que parece ser particularmente peligrosa para los hombres. He conocido colegas quienes han muerto repentinamente a esa edad, y entre ellos uno que, después de varios intentos de conseguir una cátedra, la consiguió solo unos días antes de su muerte”.

La fórmula básica en la teoría de Fliess es, en términos matemáticos, precisamente la ecuación duiofántica lineal , (para x e y enteros). Esta fórmula fue ampliamente analizada por Fliess, aunque desde una perspectiva bastante simple, y en sus obras podemos encontrar muchas tablas numéricas muy obvias. Por ejemplo, expresó los números del 1 al 28 como diferencias de múltiplos de 28 y 23, por ejemplo
, o del 1 al 51 como sumas y diferencias de múltiplos de 23 y 28.
Pero, como hemos visto más arriba, como 23 y 28 son dos números sin divisores comunes, existen números enteros x e y tal que , de hecho,
, luego todo número se puede expresarse como combinación de los números 23 y 28. Es decir, si ese es nuestro interés cualquier cuestión numérica la podemos relacionar con estos dos números, y en consecuencia, cualquier acontecimiento o información expresada de forma numérica la podremos relacionar con estos dos ciclos.
Bibliografía
1. Coin problem, WolframMathWorld
2.- Miodrag S. Petkovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
3.- Matthias Beck, How to change coins, M&M’s, or chicken nuggets: the linear diophantine problem of Frobenius, Resources for teaching Discrete Mathematics (editor Brian Hopkins), MAA, 2009.
4.- Raúl Ibáñez, Numerología, cábala y otros enigmas , Geometrian barrenako ibilaldia / Un paseo por la geometría 2007/08, UPV-EHU, 2008.
5.- Martin Gardner ¿Tenían ombligo Eva y Adán? La falsedad de la seudociencia al descubierto”, Debate, 2001.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Resumen de lecturas compartidas durante julio de 2018 | Vestigium
[…] El problema del cambio de moneda. R. Ibáñez #Matemáticas […]
La cuadratura del cuadrado: en busca del santo grial — Cuaderno de Cultura Científica
[…] hablado en el Cuaderno de Cultura Científica, como El problema de las estudiantes de Kirkman, El problema de los sellos de Sylvester, El problema de la plantación de árboles en fila, El problema de las cartas extraviadas, El […]