En este paseo que hemos iniciado en mis dos anteriores entradas del Cuaderno de Cultura Científica, sobre diferentes métodos de multiplicación que se desarrollaron a lo largo de la historia de la humanidad, y que nos ha llevado de los algoritmos que utilizaron los babilonios y los egipcios a los métodos de multiplicar que hasta recientemente han continuado utilizando los campesinos rusos, ha llegado el momento de hablar de la llamada multiplicación por celosía, o multiplicación árabe, y su relación con nuestro algoritmo de multiplicación moderno.

Quienes no pudieron leer las anteriores entradas, lo pueden hacer aquí:

1) ¿Sueñan los babilonios con multiplicaciones eléctricas?

2) Multiplicar no es difícil: de los egipcios a los campesinos rusos

Pero iniciemos esta nueva jornada del paseo en la sala 28 (dedicada a la edad moderna) del Museo Arqueológico Nacional en Madrid. Esta sala contiene el denominado Ábaco neperiano, que consiste, como se ve en la imagen de abajo, en un pequeño mueble de madera con incrustaciones de hueso con 30 cajones en su interior, en los cuales se guardan las fichas de los dos ábacos que diseñó el matemático escocés John Napier (1550-1617), cuyo nombre latinizado es Johannes Neper y que fue el matemático que inventó los logaritmos, el conocido como huesos de Napier, del que hablaremos en esta entrada, y uno de tarjetas llamado promptuario (este es el único ejemplo conocido de este tipo de ábaco). Sobre este último podéis leer el artículo de Ángel Requena de la bibliografía.

Estos dos ábacos fueron descritos por John Napier en su obra Rabdologiae, seu numerationis per virgulas libri duo: cum appendice expeditissimo multiplicationis promptuario, quibus accesit et arithmetica localis liber unus –Rabdología, numeración o varillas a través de los dos libros: apéndice con el repositorio de ejecución multiplicación, que entró un local gratuito y aritmética– (1617).

Los huesos de Napier, también conocidos como varillas o bastones de Napier, fueron desarrollados por el inventor de los logaritmos para realizar multiplicaciones, divisiones y raíces cuadradas. Los huesos de Napier consistían en una versión individualizada y particular de las tablas de multiplicar. Cada varilla contenía la tabla de multiplicar de una de las 10 cifras básicas de nuestro sistema de numeración decimal, 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9, donde el resultado de cada multiplicación individual se escribía en un cuadrado con una diagonal que separaba la parte de las decenas, arriba de la diagonal, de la parte de las unidades, debajo de la diagonal (como se puede ver en la imagen de abajo). Así, la varilla del 7, empieza con el 7 (que es 7 x 1), después 14 (que es 7 x 2), con el 1 encima de la diagonal y el 4 debajo, a continuación, 21 (7 x 3), con el 2 encima de la diagonal y el 1 debajo, y así hasta 7 x 9, que es 63.

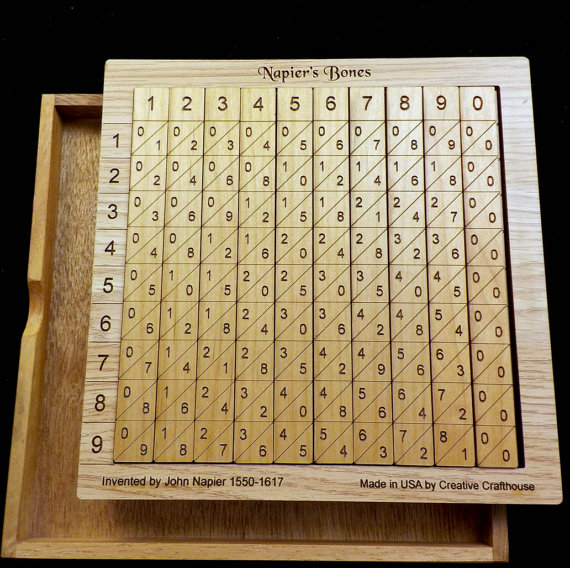
Aunque, en realidad los huesos de Napier (que deben su nombre al material con el que fueron realizados) eran diez prismas cuadrados en los que se utilizaban las cuatro caras del prisma. Cada cara tenía los múltiplos de una cifra básica, es decir, la tabla de multiplicar de ese número, de forma que en caras opuestas estaban los múltiplos de dos números cuya suma fuese 9, por ejemplo, 3 y 6. De esta forma se disponían de varias caras con los múltiplos de un mismo número, lo cual era necesario para las diferentes operaciones aritméticas, por ejemplo, para multiplicar 355 x 7 se necesitaban dos varillas con la tabla del 5.

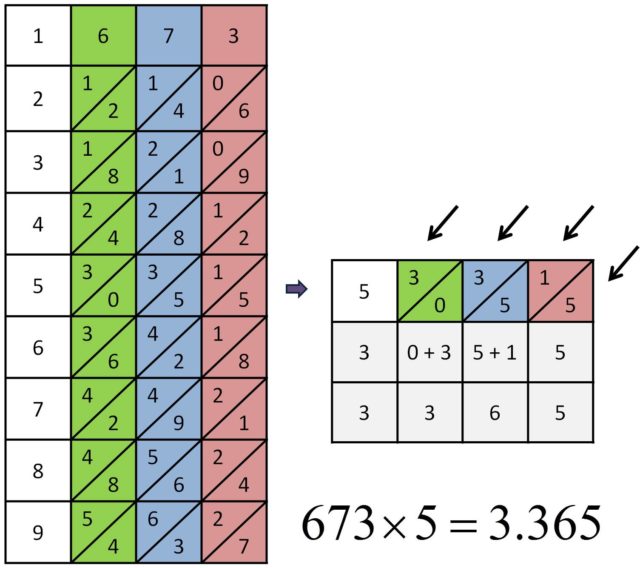
Pero veamos cómo se multiplicaba con la ayuda de los bastones de Napier. Para empezar, veamos una multiplicación sencilla, en la que uno de los números, el multiplicador, es de una sola cifra, por ejemplo, 673 x 5. Se disponen, como se muestra en la siguiente imagen, las varillas de las cifras del número que multiplicamos, el multiplicando, en el orden en el que aparecen en este 6, 7 y 3, y puestas a continuación de una varilla fija con los números del 1 al 9. Como vamos a multiplicar el número 673 por 5, consideramos la fila correspondiente al número 5, como se muestra en la imagen, es decir, 3/0, 3/5 y 1/5. Para obtener el resultado de la multiplicación, se empieza por la derecha y se van sumando en diagonal los números que aparecen en la fila del 5. Así, se obtiene el resultado, 673 x 5 = 3.365.

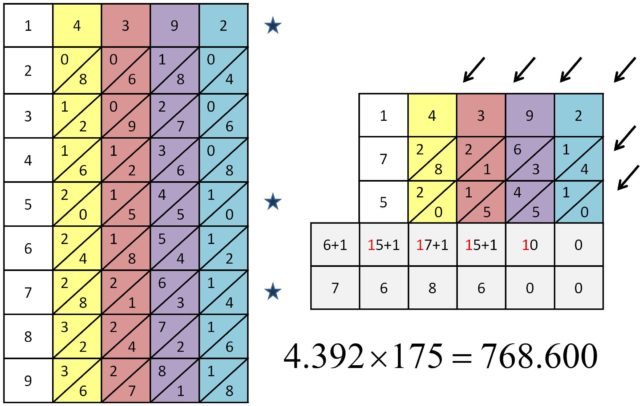
En el siguiente ejemplo consideramos números de más de una cifra. Vemos cómo se realiza la multiplicación con los huesos de Napier de los números 4.392 y 175. Como en el ejemplo anterior se disponen las varillas de las cifras del multiplicando 4.392, en el orden en el que aparecen en el número (como se muestra en la siguiente imagen). Después nos fijamos en las filas de las cifras del multiplicador, 1, 7 y 5, que deben de “considerarse” en el orden en el que aparecen en el número, 175. Finalmente, empezando por la derecha, se suman los números de cada una de las diagonales que aparecen (entendiendo que en la fila del 1, aunque solo aparezcan los números, sería como 0 arriba y la cifra abajo, en este caso, 0/4, 0/3, 0/9 y 0/2). En cada paso nos quedamos con la cifra de las unidades y sumamos a la siguiente diagonal la cifra de las decenas (la “llevada”).

Veamos cómo se obtiene el resultado. En la primera diagonal, que nos dará las unidades del resultado, solo tenemos un 0, luego 0 es la cifra de las unidades. La siguiente diagonal nos dará la cifra de las decenas, que como la suma es 4 + 1 + 5 = 10, la cifra para las decenas es 0, y nos llevamos el 1 a la siguiente diagonal. La suma de la tercera diagonal, junto con la llevada, es 2 + 1 + 3 + 4 + 5 [+1] = 16, luego el 6 está en la posición de las centenas y nos llevamos 1 para la siguiente diagonal. Y así hasta el final. En consecuencia, se obtiene que 4.392 x 175 = 768.600.

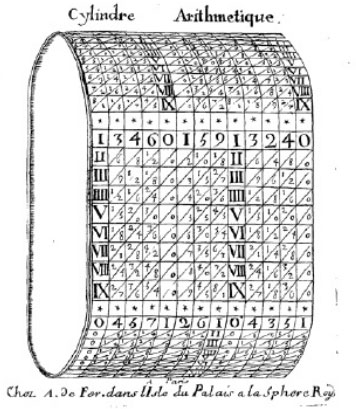
La técnica de multiplicar de los bastones de Napier fue utilizada para desarrollar algunos mecanismos de cálculo. Por ejemplo, el médico y escritor Pierre Petit (1617-1687) tomó los bastones de Napier y diseñó un cilindro aritmético, el tambor de Petit, con tiras de papel, que contenían los múltiplos de las varillas de Napier, pegadas sobre el cilindro.

Un ejemplo más avanzado es el “reloj calculador”, desarrollado por el matemático alemán Wilhelm Schickard (1592-1635) en 1623. Como se explica en la página del Museo de la Ciencia de la Universidad Pública de Navarra “se compone de dos mecanismos diferenciados: un ábaco de Napier de forma cilíndrica en la parte superior y un mecanismo en la inferior tipo pascalina para realizar las sumas parciales de los resultados obtenidos con el aparato de la parte superior. De este modo, se pueden efectuar las cuatro operaciones aritméticas fundamentales de forma manual y mecánica”. Recordemos que la “pascalina” es la primera calculadora mecánica (funcionaba a base de ruedas y engranajes), diseñada en 1642 por el matemático francés Blaise Pascal (1623-1662).

Sobre otros mecanismos de cálculo que hicieron uso de los huesos de Napier se puede leer en el volumen 3 de las Recreaciones matemáticas de Édouard Lucas.

El sistema de multiplicación de los huesos de Napier está basado en la multiplicación árabe, también llamada multiplicación por celosía. Este nombre se debe a que la cuadrícula, con diagonales, sobre la que se realiza la multiplicación recuerda a los enrejados de madera, hierro u otro material que permitían ver sin ser vistos.

Como podemos leer en el excelente libro Historia universal de las cifras (2002), de Georges Ifrah, este es un procedimiento que inventaron los árabes alrededor del siglo XIII, y que posteriormente fue transmitido a Europa, China o India. Este algoritmo fue descrito por primera vez, que tengamos conocimiento de ello, en el texto Talkhis a’mal al hisab –Exposición sumaria de las operaciones aritméticas– (1299), del matemático marroquí Ibn al-Banna al-Marrakushi al-Azdi (1256-1321). Un comentario de este libro se debe al matemático árabe del Reino nazarí de Granada Al-Qalasadi (1412-1486). Entre las obras originales de aritmética de Al-Qalasadi se encuentra su libro Hadha al-kitab kashf al-asrar fi’ilm al-ghubar –Revelación de los secretos de la ciencia aritmética- (1486), que es una simplificación de una obra anterior más completa, en el cual describe el método de multiplicar que los árabes llamaban “multiplicación en cuadro” (ad darb bi’l jadwal).

Expliquemos el método de multiplicación empleado por los árabes mediante un sencillo ejemplo, 934 x 314. Las diagonales de la multiplicación pueden tomarse en dos sentidos, pero empezaremos la explicación de este algoritmo considerando el mismo sentido que en el texto árabe de Al-Qalasadi.

Como vamos a realizar la multiplicación de dos números de 3 cifras, se realiza una cuadrícula 3 x 3, en la que se dibujan las diagonales que van de arriba a la izquierda hacia abajo a la derecha. Se escriben los dos números a multiplicar, el multiplicando, 934, escrito arriba (de izquierda a derecha) y el multiplicador, 314, en el lado derecho (escrito de abajo hacia arriba), como se muestra en la imagen.

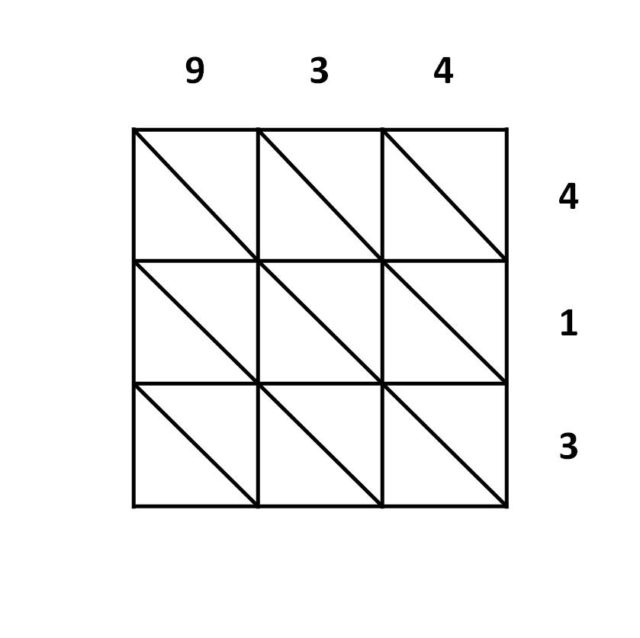
Entonces se empieza la multiplicación. En cada cuadrado de la cuadrícula 3 x 3 se escribe el producto de las cifras que determinan ese cuadrado, como en el juego de los barcos, con la cifra de las decenas debajo de la diagonal y la cifra de las unidades encima. Por ejemplo, en el cuadrado de arriba a la derecha, que se corresponde con el producto de 9 por 4, que es 36, se colocará 36. Y así con el resto, como se muestra en la imagen.

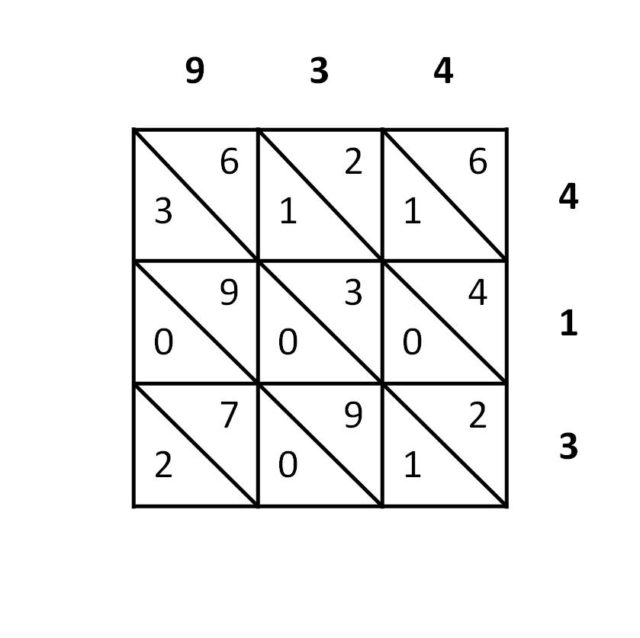
Por último, de una forma similar a la vista para los huesos de Napier, pero con las diagonales en el sentido opuesto, se van sumando las diagonales de números desde la derecha-arriba a la izquierda-abajo. La primera diagonal, que nos aporta las unidades, solo consta de un número, el 6, que será la cifra de las unidades. La siguiente diagonal nos dará las decenas, y su suma es 2 + 1 + 4 = 7. La tercera diagonal suma 6 + 1 + 3 + 0 + 2 = 12, por lo que la cifra de las centenas es 2, y el 1 se suma a la siguiente diagonal (es la “llevada”), a la de los millares. Y así se continúa con el resto. Estos resultados, 6, 7, 2, etc, que hemos ido obteniendo se van escribiendo cerca del final de la diagonal correspondiente, como se muestra en la imagen. El resultado del producto será el número formado por estas cifras que hemos ido obteniendo, leídas de izquierda a derecha y de abajo a arriba, 293.276.

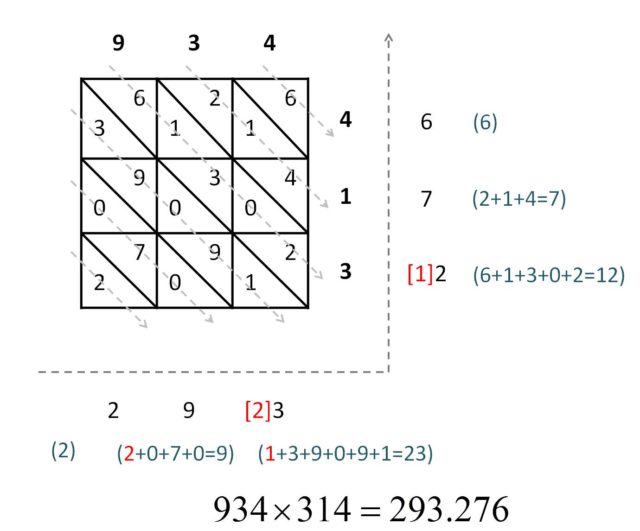
En la imagen anterior hemos escrito todos los elementos del proceso para que quede más claro, sin embargo, lo único que escribiría sobre la cuadrícula 3 x 3 una persona que tuviese que realizar la multiplicación 934 x 314 es lo siguiente:

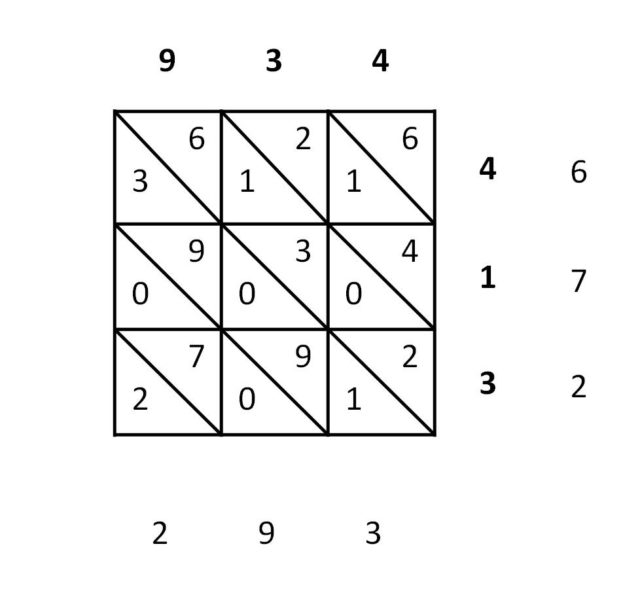
Aunque en los textos árabes se suelen escribir las sumas de las diagonales en un segmento inclinado en el vértice superior izquierdo de la cuadrícula 3 x 3, como se muestra la siguiente imagen.

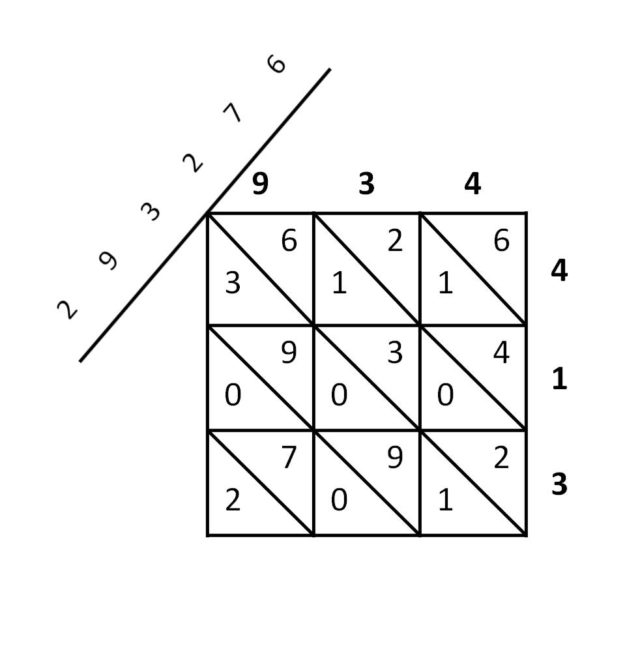
Otra disposición para este método de multiplicar es considerar las diagonales ascendentes, en lugar de descendentes, de forma que en el resultado del producto de dos cifras en la cuadrícula 3 x 3 se coloca la cifra de las decenas encima de la diagonal del cuadrado y la de las unidades debajo, y los dos números a multiplicar se colocan, el multiplicando arriba (de izquierda a derecha) como antes, pero el multiplicador, que va a la derecha, de arriba abajo, como se muestra en la imagen siguiente. Precisamente, es esta disposición la que han heredado los huesos de Napier.

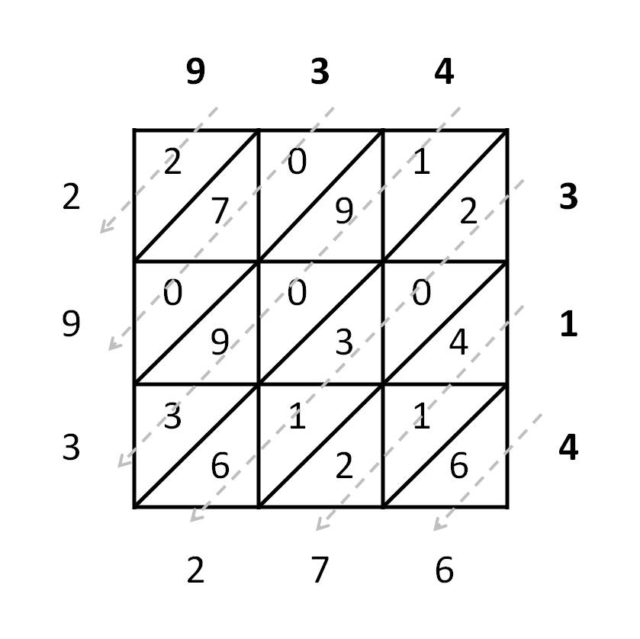
Como ya hemos comentado, este método de multiplicación fue desarrollado por los árabes alrededor del siglo XIII, quienes lo trasmitirían a la parte occidental de Europa, donde recibió el nombre de multiplicación por celosía. En Europa se describió este método, así como algunas variantes del mismo, en un tratado anónimo sobre aritmética publicado en Treviso en 1478, Larte de labbacho (conocido también como Aritmética de Treviso). También se describe en la obra Summa de arithmetica, geometría, proportioni et proportionalita precipitevolissimevolmente (1494) del matemático italiano Luca Pacioli (aprox. 1445-1517). Aunque, como podemos leer en el libro A History of Algorithms: From the Pebble to the Microchip (1999), la primera referencia escrita sería un tratado inglés, escrito en latín alrededor del año 1300, Tractatus de minutis philosophicis et vulgaribus, en el que aparece la multiplicación de 4.569.202 por 502.403.

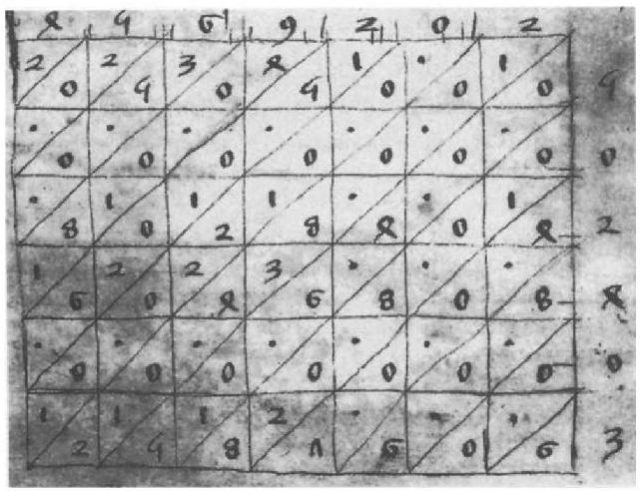
Este método también llegó a China. Según el libro A History of Algorithms: From the Pebble to the Microchip aparece por primera vez explicado en el texto Jiuzhang suanfa bilei daquan –Suma de los métodos de cálculo de los Nueve Capítulos que consisten en problemas resueltos por analogía con problemas tipo- (1540), de Wu Jing.

Sin embargo, aunque también se suele denominar a este algoritmo de multiplicación bajo el nombre de multiplicación hindú, lo cierto es que no hay constancia de su uso en la India hasta mediados del siglo XVII, que aparece explicado en el comentario Ganitamañjari (1658) del matemático indio Ganesha sobre el libro Lilavati (1150) del matemático indio Bhaskara II.

Volviendo a la imagen de las páginas de la Aritmética de Treviso (1478), se encuentra en la misma imagen una variación de la multiplicación por celosía, en la que en lugar de escribir todos los detalles del procedimiento de la multiplicación árabe, se limita a escribir en cada cuadrado de la cuadrícula únicamente las unidades de las multiplicaciones intermedias, por lo que la persona que realiza la operación debe de tener cuidado con las decenas de dichas multiplicaciones, que ahora no se escriben pero que se añaden al resultado del siguiente cuadrado (a la izquierda), las “llevadas”. Esto último se corresponde, en el método de multiplicación árabe, a añadir la “llevada” a la siguiente diagonal.

A continuación, mostramos en diferentes etapas el ejemplo de la multiplicación 934 x 314 mediante este método (las diagonales que se pintan en la siguiente imagen pertenecen a la explicación, pero no aparecían en el desarrollo de la multiplicación).

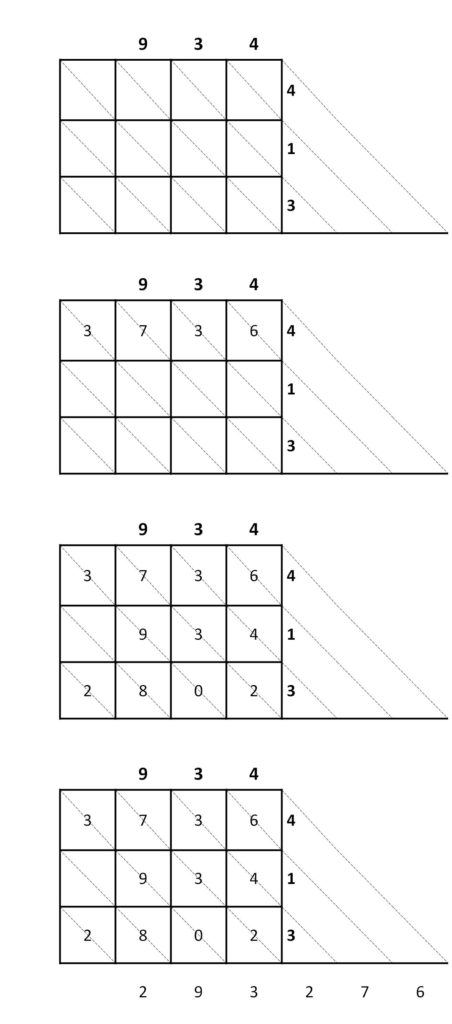
Esta versión tendría su variante con las diagonales en el sentido contrario y con el multiplicador escrito en el lateral ahora de arriba hacia abajo.

Y la última variante, que también aparece en Larte de labbacho (1478) y que habría empezado a utilizarse a finales del siglo XV, simplifica las anteriores. Para empezar se traza una línea horizontal y sobre ella el multiplicante, después se escribe el multiplicador debajo a la derecha y escrito de abajo hacia arriba (como en el algoritmo árabe o la variante descrita en la anterior imagen), pero siguiendo sus cifras una línea inclinada hacia la derecha. El proceso es similar al anterior, como vemos en la imagen.

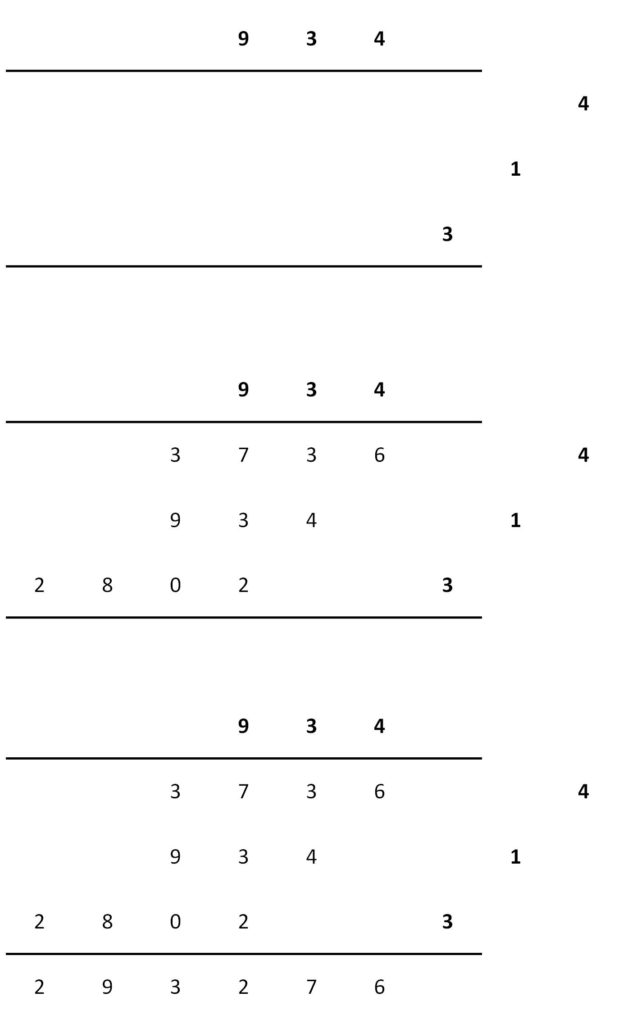
Este método, salvo por el hecho de que nosotros colocamos el segundo número debajo del primero, es exactamente el algoritmo que utilizamos para multiplicar. Por lo tanto, nuestro método de multiplicación, el que tú y yo utilizamos, el que nos enseñaron en la escuela, es una variación de la multiplicación árabe que se desarrolló a finales del siglo XV.

Bibliografía

1.- Museo Arqueológico Nacional

2.- Frank J. Swetz, Mathematical Treasure: John Napier’s Rabdologiae, Mathematical Association of America

3.- Nelo Alberto Maestre e Inmaculada Conejo (DIVERMATES), Ábaco neperiano, Museo Arqueológico Nacional, octubre 2014.

4.- Ángel Requena Faile, Una joya de la corona: el ábaco neperiano, mateturismo [xxx].

5.- Georges Ifrah, Historia universal de las cifras, Espasa, 2002.

6.- Calculadora Schickard, Museo de la Ciencia de la Universidad Pública de Navarra

7.- Éduoard Lucas, E., Recreaciones matemáticas, vol. 1 – 4, Nivola, 2007 y 2008.

8.- Jean-Luc Chabert, A History of Algorithms, From Pebble to Microchips, Springer, 1999.

9.- A S Saidan, Biography in Dictionary of Scientific Biography (New York 1970-1990).

10.- Mathematical Art: «The End of Simple Multiplication«, 1814, JF Ptak Science Books LLC, Post 982

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica