El 23 de septiembre de 1999, tras más de nueve meses de viaje entre la Tierra y Marte, la sonda espacial Mars Climate Orbiter se desintegró al entrar en contacto con la atmósfera del planeta rojo. La Mars Climate Orbiter, que tenía un coste de 125 millones de dólares y formaba parte de un programa espacial con un presupuesto de más de 300 millones de dólares, tenía como objetivo estudiar el clima y las condiciones atmosféricas del planeta Marte, así como servir de apoyo para la transmisión de datos de la Mars Polar Lander, ambas parte de la misión espacial Mars Surveyor’98.

Como puede leerse en el informe de la investigación que se realizó sobre el accidente de la Mars Climate Orbiter en noviembre de 1999 –Mars Climate Orbiter Mishap Investigation Board, Phase I Report– el accidente tuvo lugar por el uso de datos en el sistema imperial de medidas cuando se tenían que haber utilizado los datos en el sistema métrico decimal.

Desde la NASA se estaban realizando los cálculos para el impulso que debían de producir los motores, cada vez que se encendían para corregir la trayectoria del viaje a Marte de la Mars Climate Orbiter, en libras de fuerza multiplicado por segundos (lbr·s), es decir, en el sistema inglés de medidas, mientras que el software de los ordenadores de la sonda operaban en newtons·segundo (N·s), es decir, en el Sistema Internacional de Medidas. Así, cada vez que se encendían los motores para ir corrigiendo la trayectoria se iba acumulando un error en la misma, debido a esa discrepancia en los datos.

Al llegar a Marte, la sonda debía estar a una altura de 226 km sobre la superficie del planeta rojo, a partir de ese momento se realizaría una maniobra de aproximación hasta quedar estacionada en una órbita alrededor del planeta, sin embargo, la sonda pasó a tan solo 57 kilómetros de altura, destruyéndose por el contacto con la atmósfera.

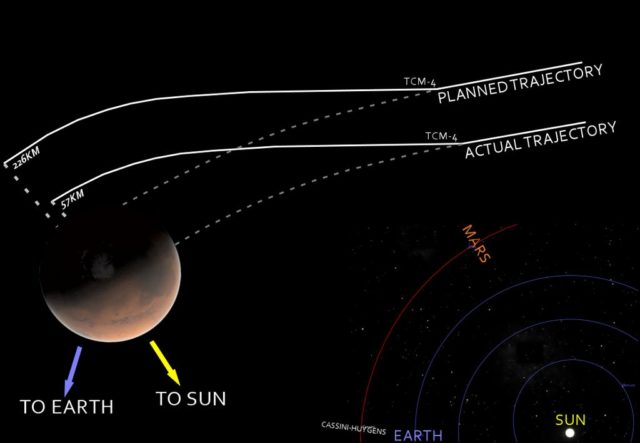
Pero veamos de qué magnitud fue el fallo que se cometió al mezclar ambos sistemas de medidas. Imaginemos que el cálculo realizado por la NASA en Tierra ofrecía la información de que el impulso que debía darse al motor de la sonda espacial era de 10.000.000 libras (de fuerza) segundo, pero el ordenador de la sonda interpretaba ante esta información, puesto que su software trabaja en el sistema internacional de medidas, que eran 10.000.000 Newtons segundo. Teniendo en cuenta que 1 libra (de fuerza) son 4,5 Newtons, se tendría que

10.000.000 Newtons·segundo = 10.000.000 x (1/4,5) = 2.222.222 libras·segundo,

Es decir, se habría producido un déficit en el impulso de más de 7 millones de libras (de fuerza) segundo. Solo un 22% del impulso que se tenía que haber generado.

Este es solo uno de los ejemplos de los errores que se han producido en las últimas décadas por el uso simultáneo de dos sistemas de medidas distintos, el sistema internacional y el sistema imperial de medidas.

Antes de la revolución francesa, 1789, la situación de los sistemas de medidas era caótica. Cada país, pero lo que es peor aún, cada región dentro de un mismo país, tenía sus propios sistemas de medidas, pero incluso en ocasiones compartían el mismo nombre, lo que convertía en un problema una simple compra y venta de alimentos, utensilios o ganado en una feria comarcal, y en general, dificultaba las transacciones comerciales, la investigación científica y todo tipo de comunicación.

El escritor inglés Arthur Young (1741-1820) en la versión extendida, de cuatro volúmenes, de sus viajes por Francia, Travels during the years 1787, 1788, & 1789: undertaken more particularly with a view of ascertaining the cultivation, wealth, resources, and national prosperity of the Kingdom of France (W. Richardson,1792), comenta “en Francia, la infinita perplejidad que causa la profusión de medidas excede toda comprensión. No solo difieren en cada provincia, sino en cada distrito, y casi en cualquier población”.

En el libro La medida de todas las cosas (2003), su autor Ken Alder escribe que “algunos contemporáneos calculaban que, bajo la cobertura de unos ochocientos nombres, el Antiguo Régimen de Francia utilizaba la asombrosa cifra de unas doscientas cincuenta mil unidades diferentes de pesos y medidas”.

O en el libro Outlines of the evolution of weights and measures and the metric system (Macmillan, 1906), de William Hallock y Herbert T. Wade, los autores indican que “A finales del siglo pasado (dieciocho), en diferentes partes del mundo, la palabra “libra” se aplicaba a 391 unidades diferentes de peso y la palabra “pie” a 282 unidades diferentes de longitud”.

Como es lógico, en la antigüedad cada región había desarrollado sus propios sistemas de medida, en muchas ocasiones basados en el cuerpo humano (por lo que la medida dependía del tamaño medio de los habitantes de esa región) o en cuestiones culturales específicas de la región donde se establecían, pero el mundo, su cultura, su ciencia y su economía, cada vez se hizo más global y las diferentes medidas empezaron a chocar unas con otras.

Como hemos visto, la situación antes de la revolución francesa de las unidades de medida en Europa, y en el mundo, era un auténtico desastre. Como decía el matemático y filósofo Nicolás de Condorcet (1743-1794) en sus Observaciones sobre el Libro XXIX del “Espíritu de las Leyes” de Montesquieu (1793), “la uniformidad de los pesos y medidas solo pueden desagradar a los empleados de los tribunales de justicia que teman ver disminuido el número de pleitos, y a aquellos comerciantes a los que la disminución de beneficios va a afectar, en cuanto a que contribuye a convertir las transacciones comerciales fáciles y simples”.

Aunque ya habían existido intentos anteriores, tras la Revolución Francesa se ponen las bases para crear un sistema de medidas universal. En palabras de Condorcet “para todos los pueblos, para siempre”. Para tal fin, en 1790, se crea la Comisión de Pesos y Medidas, constituida por los científicos Jean-Charles Borda (1733-1799), Joseph-Louis Lagrange (1736-1813), Pierre-Simon Laplace (1749-1827), Gaspard Monge (1746-1818) y Nicolás Condorcet. Para alcanzar la universalidad, el sistema de medidas debía ser decimal (aunque inicialmente también se valoró la posibilidad del sistema duodecimal), sus valores derivados de la naturaleza (por ejemplo, el metro tomaría el valor de “una diezmillonésima parte de la circunferencia de la Tierra”), las unidades de medida derivadas deberían basarse en potencias de las unidades básicas y se debían utilizar prefijos para designar los múltiplos y submúltiplos de las unidades.

La historia del sistema métrico decimal es apasiónate y empieza con la aventura de la medición del meridiano que pasa por París para definir determinar el valor del metro, aunque este no es el objetivo de esta entrada. Sobre este tema existen buenos libros, como El metro del mundo (Anagrama, 2003) de Denis Guedj o el mencionado La medida de todas las cosas (2003), de Ken Alder.

Tras la instauración en Francia, no sin problemas, del Sistema Métrico Decimal, muchos otros países del entorno, así como de Latinoamérica, empezaron a adoptar a lo largo del siglo XIX este sistema de medidas universal, Países Bajos, España, Alemania, Italia, Portugal, Noruega, Suecia, el Imperio Austro-Húngaro, Finlandia, Perú, México, Venezuela, entre muchos otros.

En 1875, diecisiete países firmaron la Convención del metro, “anhelando la uniformidad y la precisión internacionales en los estándares de pesos y medidas”, y se crearon las organizaciones internacionales para velar por la uniformidad de los pesos y medidas a lo largo de todo el mundo, la Oficina Internacional de Pesas y Medidas, el Comité Internacional de Pesas y Medidas y la Conferencia General de Pesos y Medidas. Poco a poco los diferentes países del mundo se fueron sumando a estas organizaciones y adoptando el sistema métrico decimal.

En la Conferencia General de Pesos y Medidas de 1960 se estableció finalmente el Sistema Internacional de Unidades. Las unidades básicas del Sistema Internacional (SI) son siete, el metro (longitud), el kilogramo (masa), el segundo (tiempo), el amperio (corriente eléctrica), el kelvin (temperatura termodinámica), el mol (cantidad de sustancia) y la candela (intensidad lumínica). Y de estas unidades básicas se derivan las otras unidades, como por ejemplo, el hercio (frecuencia), el Newton (fuerza), el pascal (presión), el julio (trabajo), etc.

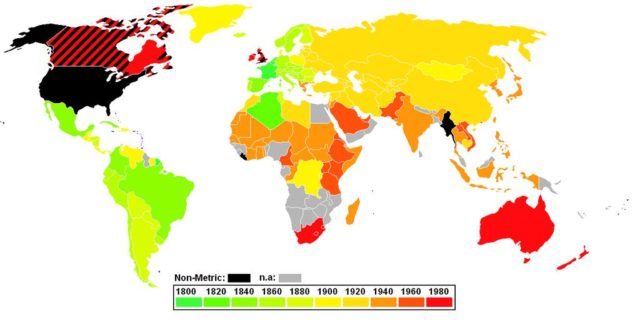
Como se muestra en el mapa anterior, en la actualidad solamente hay tres países que no se han sumado al Sistema Internacional de Unidades, que son Estados Unidos, Liberia y Birmania (Myanmar), aunque estos dos últimos están en el proceso de adopción del Sistema Internacional. Por otra parte, países que han adoptado recientemente el SI, como Gran Bretaña o Canadá, siguen utilizando su viejo sistema de medidas en muchos ámbitos de su vida, el sistema imperial (o inglés) de medidas, que es el que continúa utilizando Estados Unidos en la actualidad.

Entre las unidades del Sistema Imperial de Medidas están las yardas (en longitud), los acres (en área), los galones (en volumen), las libras (en masa), entre otras.

A continuación, veremos otros ejemplos de errores y catástrofes producidos por la confusión en el uso de estos dos sistemas de medidas, el Sistema Internacional y el Sistema Imperial. Estos ejemplos aparecen, entre otros sitios, referenciados en la página web de una asociación que existe en EE.UU. para la promoción del Sistema Internacional de Medidas fundada en 1916, la U. S. Metric Association.

El primer ejemplo que traemos a esta entrada, aparte del inicial sobre la Mars Climate Orbiter, es un ejemplo sencillo de confusión entre kilogramos y libras de los que seguramente se habrán producido muchos, pero que no suelen ser recogidos en los medios de comunicación, a diferencia de este.

En 2001, se publicó en el San Francisco Business Times la noticia “Fabricantes, los exportadores piensan en métrico”. En ella se contaba la historia de un empresario norteamericano, Carlos Zambello, que había vendido un cargamento de arroz salvaje a un cliente japonés y como en la transacción había habido una cierta confusión, causándoles cierto bochorno, por no hablar de las pérdidas económicas.

En concreto, a la compradora japonesa se le ofreció el arroz salvaje a un precio de 39 centavos… el problema es que ella estaba entendiendo que la oferta era de 39 centavos el kilogramo, mientras que el vendedor se estaba refiriendo a 39 centavos la libra. La cuestión es que como 1 kilogramo equivale a 2,2 libras, el coste del trigo salvaje era realmente de 85,8 centavos el kilogramo, mucho más de lo que pensaba la compradora, 39 centavos el kilogramo.

Una vez que se dieron cuenta del malentendido, el gerente general de la compañía The Wild Rice Exchange, Carlos Zambello, acabó aceptando que el precio del arroz salvaje vendido fuera su precio de coste, puesto que en el otro lado tenían a un buen cliente desde hacía muchos años, sin obtener ningún beneficio en la transacción, mientras que el comprador japonés, aunque pagó menos de lo que era su precio real, acabó aceptando pagar el precio de coste, más de lo que había pensado que era su precio de compra.

Otra historia con un malentendido entre kilogramos y libras se recogió en el periódico Los Angeles Times, en febrero de 2001. Bajo el titular “Mismeasure for measure” (que podríamos traducir como “Incorrecta medida para medir”) se contaba como el Zoológico de Los Ángeles había prestado su vieja tortuga galápago Clarence, de 75 años de edad, al Exotic Animal Training and Management Program de la Universidad de Moorpark (Moorpark College). Pero, durante la primera noche de la vieja tortuga en su nuevo hogar, esta se había escapado echando abajo uno de los postes de la cerca en la que se encontraba.

El Zoológico de Los Ángeles había avisado que la tortuga galápago era grande y que se necesitaba una cerca para un animal de un peso de 250, que es lo que construyó la Universidad de Moorpark. El problema estaba en que desde la institución universitaria habían interpretado que se estaba hablando de 250 libras, cuando realmente hablaban de 250 kilogramos, o lo que es lo mismo, unas 550 libras.

Nuestro siguiente ejemplo, nos lleva a uno de los últimos países en adoptar el Sistema Internacional de Medidas, Canadá, cuyo proceso de metrización empezó en la década de los años 1970, aunque no ha sido desarrollado completamente.

En julio de 1983 el avión Boeing 767-200 del vuelo 143 de Air Canadian se quedó sin combustible a mitad de su vuelo entre Montreal y Edmonton, debido a que la tripulación calculó mal el fuel que necesitaban para el viaje (junto con una serie de fallos en el sistema indicador de la cantidad de combustible del avión). Por suerte, se pudo realizar un aterrizaje de emergencia en una antigua base militar.

El error en el cálculo de la carga de combustible necesaria se produjo debido a que el personal no tenía una formación adecuada en el sistema métrico decimal que se acababa de adoptar en Canadá, sustituyendo al sistema imperial.

La tripulación sabía que se necesitaban 22.300 kilogramos de fuel para realizar el viaje entre Montreal y Edmonton. Pero el avión ya tenía 7.682 litros en sus tanques, por lo que había que calcular cuánto fuel extra era necesario cargar en los tanques para realizar el viaje.

Teniendo en cuenta que el peso de 1 litro de fuel es de 0,803 kilogramos, entonces el peso del fuel que tenía ya el avión era de 7.682 litros x 0,803 kg/litro = 6.169 kg.

Por lo tanto, el avión necesitaba que se le añadieran a sus tanques 22.300 – 6.169 = 16.131 kg.

Luego, ¿cuántos litros de fuel debían de cargarse en el avión? Teniendo en cuenta de nuevo, que cada litro pesa 0,803 kilogramos, la cantidad de fuel necesario era de 16.131 kg x (1 litro /0,803 kg) = 20.088 litros.

La tripulación, sin embargo, tuvo en cuenta el factor de conversión de 1,77 (en lugar de 0,803), que era el que habían estado utilizando hasta entonces ya que 1 litro de fuel pesa 1,77 libras (tengamos en cuenta que 1 kilogramo son 2,205 libras, luego 0,803 kilogramos son 1,77 libras).

Por lo tanto, esta fue la cuenta que realizaron…

1.- el peso del fuel que aún quedaba en los tanques del avión era…

7.682 x 1,77 = 13.587 “kilogramos” (en realidad eran libras)

2.- el peso del fuel que había que añadir era…

22.3000 – 13.587 = 8.713 “kilogramos”

3.- luego, ¿cuántos litros calcularon que había que cargar en los tanques?

8.713 kg x (1 / 1,77) = 4.923 litros (el factor a utilizar debía de ser litros/kilogramo, aunque el dato que utilizaban de nuevo era litros/libra, 1/1,77)

En conclusión, cargaron solamente 4.923 litros de los 20.088 litros que realmente eran los necesarios.

En abril de 1999 el avión McDonnell Douglas MC-11F en su vuelo 6316 de Korean Air Cargo de Shanghai a Seoul se estrelló, muriendo las tres personas de la tripulación y otras 5 personas en tierra, así mismo, hubo 37 heridos en tierra.

Después del despegue el avión debía subir a una altura de 1.500 metros (que son 4.900 pies, puesto que 1 metro equivale a 3,28 pies). Cuando el avión subió a 4.500 pies (casi a 1.400 metros), el primer oficial informó al capitán de que la altura del avión debía ser de 1.500 pies (confundiéndose con los 1.500 metros que realmente debía de tener), pensando por lo tanto que el avión estaba 3.000 pies más arriba de lo que debía. Como consecuencia el capitán puso bruscamente el avión en descenso para intentar poner al avión a una altura de 1.500 pies (que son unos 460 metros), como consecuencia de esta maniobra el avión se volvió incontrolable y terminaría estrellándose en una zona industrial a 10 kilómetros del aeropuerto.

Los deportistas norteamericanos suelen sufrir su aislamiento del Sistema Internacional de Medidas en las competiciones deportivas, en particular, en los Juegos Olímpicos. Un ejemplo de este problema fue el no reconocimiento mundial de un record en atletismo. La atleta Carol Lewis realizó un salto de longitud que parecía ser un record mundial en los campeonatos NCAA Men’s and Women’s Indoor Track Championship celebrados en Pontiac, Michigan, en 1983. Sin embargo, su marca no fue reconocida como un record oficial, puesto que para que se considere un record oficial las medidas deben tomarse en el sistema internacional, es decir, en el sistema métrico decimal.

En Diciembre de 2003, el tren de la montaña rusa Space Mountain que se encuentra en el parque temático Tokyo Disneyland descarriló cuando llegaba a la estación. El descarrilamiento se produjo debido a la ruptura de un eje del tren. Por suerte, no hubo que lamentar ninguna desgracia y todo quedó en un susto.

Como resultado de la correspondiente investigación para aclarar los motivos del accidente, se descubrió que el eje se había construido con un diámetro más pequeño que las especificaciones de los planos del diseño. En el año 1995 se habían cambiado las medidas de los planes maestros para la construcción de la Space Mountain, del sistema imperial al sistema internacional de medidas. Cuando se fue a construir la Space Mountain de Tokyo en 2002, se tomaron los valores de las medidas de los planos del diseño anteriores a 1995.

Según el informe, mientras que en los planos del diseño se especifica que el espacio entre el eje y su cojinete debía de ser de 0,2 mm, realmente era de alrededor de 1 mm, lo cual creó una mayor vibración que hizo que se rompiera el eje. Recordemos que 1 pulgada son 2,54 centímetros, o recíprocamente, 1 cm equivale a 0,3937 pulgadas.

Y para terminar, un ejemplo relacionado con el volumen. En 2004 a un niño se le estuvo dando 5 veces la dosis prescrita por el médico de Zantac Syrup, un medicamento para reducir la producción del ácido estomacal, hasta que un mes más tarde el médico descubrió la confusión. Afortunadamente, el error no tuvo ninguna consecuencia grave para el bebé.

El médico había prescrito una dosis de 0,75 mililitros, dos veces al día, pero el farmacéutico escribió en el bote del medicamento “administrar 3/4 de cucharadita (teaspoon) dos veces al día”. Teniendo en cuenta que esta medida de Estados Unidos, 1 “cucharadita” (u.s. teaspoon), tiene la equivalencia en el sistema métrico decimal de 4,9 mililitros, se le estuvieron suministrando 3,675 mililitros, dos veces al día, es decir, casi 5 veces la dosis prescrita.

Bibliografía

1.- U.S. Metric Association.

2.- Mars Climate Orbiter Mishap Investigation Board, Phase I Report, November 10, 1999

3.- Some Famous Unit Conversion Errors, Space Math, NASA

4.- Arthur Young, Travels during the years 1787, 1788, & 1789: undertaken more particularly with a view of ascertaining the cultivation, wealth, resources, and national prosperity of the Kingdom of France, W. Richardson,1792.

5.- Ken Alder, La medida de todas las cosas, Taurus/Santillana, 2003.

6.- William Hallock y Herbert T. Wade, Outlines of the evolution of weights and measures and the metric system, Macmillan, 1906.

7.- Nicolás de Condorcet, Observaciones sobre el Libro XXIX del “Espíritu de las Leyes” de Montesquieu, 1793.

8.- Denis Guedj, El metro del mundo, Anagrama, 2003.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica