En su Traité du triangle arithmétique (Tratado del triángulo aritmético, publicado por primera vez en 1654), Blaise Pascal iniciaba su texto con una página en la que dibujaba su triángulo aritmético (ver figura 1). Le seguían casi un centenar de páginas en las que el matemático daba diecinueve propiedades de ese triángulo, bastante sencillas de demostrar en general. Pascal probaba algunas de ellas, otras las mostraba mediante un ejemplo y otras quedaban solo enunciadas.

Ese triángulo, conocido hoy en día como triángulo de Pascal –aunque ya era conocido en el siglo X–, proporciona una manera de ordenar los coeficientes binomiales. Recordemos que el coeficiente binomial C(n,k) es el número de grupos de k objetos que pueden elegirse en un conjunto formado por n objetos. En la figura 2 puede verse su expresión:

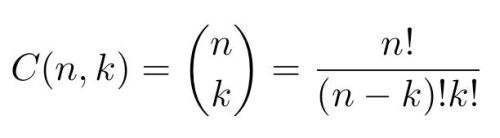
Los coeficientes binomiales también pueden calcularse por recurrencia, utilizando la llamada fórmula de Pascal que aparece debajo.

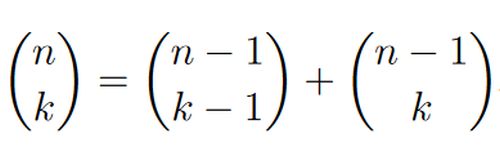
El triángulo de Pascal P_n es el reordenamiento de los coeficientes binomiales desde el C(0,0) hasta el C(n,n), de manera que en la fila m aparecen (y en ese orden):

C(m,0), C(m,1), C(m,2), …, C(m,m-1) y C(m,m).

El triángulo de Sierpinski es un conjunto fractal que se construye de manera recurrente como se indica a continuación: se toma un triángulo equilátero ‘lleno’, S₀, al que se le quita el pequeño triángulo formado al unir las mitades de sus tres lados (ver la figura 4). Obtenemos S₁ formado por tres triángulos ‘llenos’ sobre los cuales se realiza el mismo proceso que acabamos de describir. Logramos así una figura formada por nueve triángulos llenos, S₂, a los que se les vuelve a aplicar el mismo procedimiento.

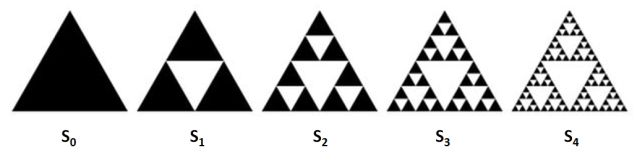
Iterando este procedimiento indefinidamente, se obtiene el triángulo de Sierpinski, que lleva el nombre del matemático Wacław Sierpiński, quien lo describió en 1915 (aunque aparece como elemento decorativo –alguna etapa de su construcción– mucho antes).

¿Existe alguna relación entre estos dos triángulos? El primero, el de Pascal, se construye de manera combinatoria y el segundo, el de Sierpinski, de manera geométrica… ¿pueden vincularse de alguna manera?

Como se observa en la figura 6, todos los triángulos ‘llenos’ que modelan cada S_n pueden rellenarse con coeficientes binomiales impares. Y, a su vez, cada coeficiente binomial impar puede colocarse dentro de uno de los triángulos ‘llenos’ en determinada etapa de la iteración en la construcción del triángulo de Sierpinski.

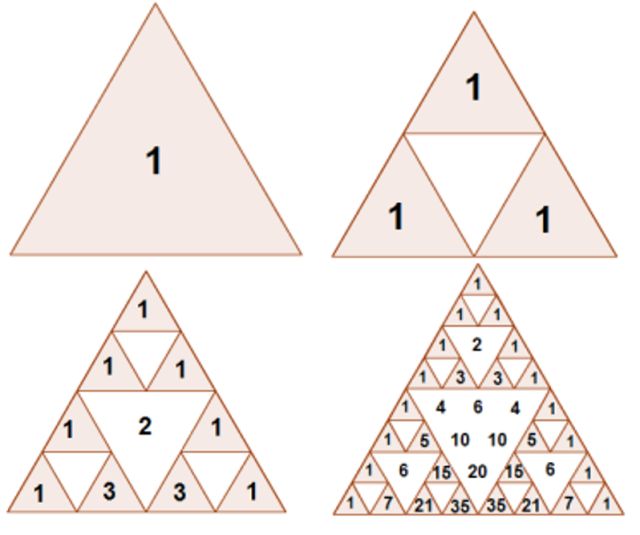
El enunciado preciso que proporciona la propiedad que acabamos de mostrar es la siguiente: “Para cada número natural n, el triángulo de Sierpinski S_n se corresponde con el triángulo de Pascal de 2ⁿ filas, del que se han eliminado los coeficientes pares”.

Observar que este resultado ofrece otra manera de construir S_n. En efecto, bastaría con dividir un triángulo equilátero en triángulos equiláteros más pequeños, de modo que cada lado del triángulo original se divida en 2ⁿ partes iguales. Superponiendo el triángulo de Pascal de 2ⁿ filas, bastaría con colorear únicamente los pequeños triángulos correspondientes a los coeficientes binomiales impares…

¡Una bella y curiosa propiedad!

Referencias

• Blaise Pascal, Traité du triangle arithmétique, avec quelques autres petits traitez sur la mesme matière. Par Monsieur Pascal, G. Desprez, 1665 (en Gallica).
• Sierpiński et Pascal sont dans un triangle, Blogdemaths, 16 julio 2013

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.