Compartiendo un rumor
Compartimos debajo un ¿rumor?… ¡No! De momento, un problema propuesto en 2001 en Crux Mathematicorum, revista científica publicada por la Sociedad Canadiense de Matemáticas, y que contiene problemas matemáticos para estudiantes de secundaria y pregrado.

Ana, Beatriz, Carlos, David, Elena, Fátima, Guillermo, Hugo e Inés forman parte de la comisión de estudiantes de su Facultad. Se reúnen con poca frecuencia y, además, al ser sus ideas bastante diferentes, no conversan demasiado.
En la siguiente tabla se resumen las relaciones entre estas nueve personas (cada una está representada por la inicial de su nombre): 0 significa que las dos personas no se hablan y 1 que lo hacen con frecuencia.
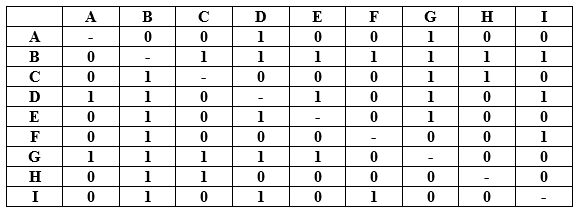
Si numeramos a Ana, como iniciadora del rumor con un 1, y Elena fue la novena y última del grupo en escuchar el rumor, ¿quién fue la quinta persona en enterarse de él?
La solución propuesta por la propia revista solo requiere un poco de lógica para usar de la mejor manera los datos proporcionados.
En efecto, sabemos que Ana inicia el rumor y que Elena es la última persona que se entera.
Entre las demás personas Fátima y Hugo son los que menos relaciones tienen, al hablarse solo con dos de las personas del grupo. Así que empezaremos por ellos.
Según los datos de la tabla, a Fátima le debe llegar el rumor vía Inés y se lo cuenta después a Beatriz (IFB) o viceversa (BFI). Del mismo modo, Hugo se lo escucha a Beatriz y se lo transmite después a Carlos (BHC) o viceversa (CHB).
Al unir estos dos fragmentos del itinerario del rumor, obtenemos la serie de cinco personas (CHBFI) o (IFBHC). Además, ninguno de estos dos posibles caminos recorridos por el rumor se une con A o con E, ya que Ana no se habla ni con Carlos ni con Inés, y lo mismo sucede con Elena.
Por el anterior comentario, David y Guillermo deben ir necesariamente en los extremos de (CHBFI) o (IFBHC). Pero, David no se habla con Carlos, aunque si con Inés. Guillermo, al contrario, se habla con Carlos, pero no con Inés.
Así, podemos asegurar que el orden de transmisión del rumor entre estas siete personas –excluyendo a Ana y Elena– ha sido (GCHBFID) o (DIFBHCG). Añadiendo a Ana y Elena a esta serie, quedaría que el rumor iniciado por Ana ha llegado a Elena de alguna de estas dos maneras: (AGCHBFIDE) o (ADIFBHCGE).
De cualquiera de los dos modos, la quinta persona en enterarse del rumor ha sido Beatriz.
Notas:
Visto en: The Grapevine, Futility Closet, 16 noviembre 2017
Extraído de: R.E.Woodrow, The skoliad Corner no. 8, Crux Mathematicorum 27:3 (Abril 2001), pág. 194
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
Nota del editor: El 23/11/17 la autora alteró la redacción de dos párrafos para hacerlos más precisos. Esta alteración no altera el contenido general del texto.
