Las personas que han visitado durante las últimas semanas el Museo Guggenheim de Bilbao han tenido la suerte de poder disfrutar de una exposición interesante e inspiradora, “Anni Albers, tocar la vista” (6 de octubre de 2017 – 14 de enero de 2018). Esta exposición nos acerca a la obra de la artista de origen alemán, afincada en Estados Unidos, Anni Albers (1899-1994), quien seguramente sea la artista textil más importante del siglo XX, aunque también trabajó otras técnicas como el grabado, la pintura o el diseño de joyas.

La exposición está compuesta por alfombras y colgaduras textiles, telas, diagramas geométricos, dibujos y estudios para el diseño de obras textiles, joyas, aguatintas, litografías, serigrafías e impresiones offset, acuarelas y otros tipos de pinturas, en las cuales la geometría juega un papel fundamental.

Las personas que deseen más información sobre la exposición pueden visitar la página del Museo Guggenheim-Bilbao Anni Albers, tocar la vista o ver los cuatro videos que el museo ha colgado en su canal de youtube y que están aquí.

La visita a la exposición Anni Albers, tocar la vista fue una experiencia enriquecedora. Descubrí a una artista excepcional y disfruté de unas creaciones artísticas increíbles. Tengo ganas de volver para sumergirme de nuevo en el arte de Anni Albers, y descubrir más sobre los procesos creativos, claramente conectados con las matemáticas, de esta artista. Aunque muchas de las obras de la exposición despertaron la curiosidad de mi mirada matemática, me gustaría destacar aquí la serie de obras dedicadas a los “nudos”, como su litografía Enredada (1963),

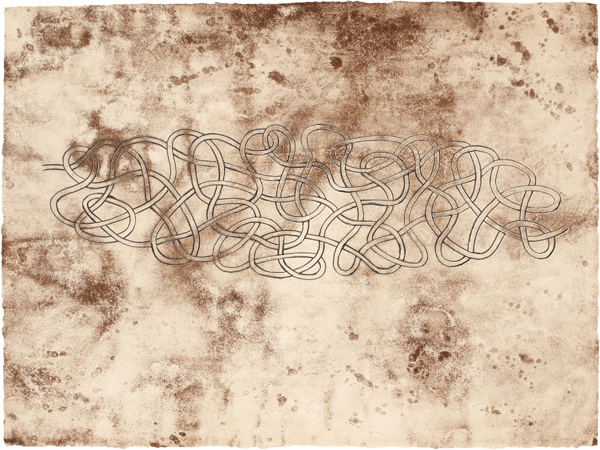
o su, también litografía, Sin título (1963),

que rápidamente me recordaron a la teoría de nudos de las matemáticas. De hecho, esta última obra me hizo recordar la fotografía realizada por un microscopio electrónico de un fragmento anudado del ácido desoxirribonucleico, ADN, cuyo estudio es uno de los campos de aplicación de la teoría de nudos.

La teoría de nudos, que ya mencionamos brevemente en la entrada del Cuaderno de Cultura Científica La topología modifica la trayectoria de los peces, es una rama de la topología que se dedica al estudio matemático de los nudos, que surgió en el siglo XX, aunque tiene sus orígenes en el siglo XIX con el trabajo de matemáticos como el alemán Carl Friedrich Gauss (1777-1855), su alumno Johann B. Listing (1808-1882) o el inglés Peter G. Tait (1831-1901). La teoría de nudos tiene numerosas e importantes aplicaciones fuera de las matemáticas, como por ejemplo en biología molecular, medicina, mecánica estadística, física de polímeros y de cristales, teoría física de cuerdas, criptografía, o ciencias de la computación.

La idea matemática de nudo es una abstracción matemática de lo que sería un nudo físico. Se coge una cuerda, se anuda de una forma más o menos enrevesada y se pegan los extremos. Desde el punto de vista matemático nos interesa la línea cerrada que describe la cuerda, sin tener en cuenta el grosor de la misma, es decir, un nudo es una línea curva anudada cerrada, que no tiene puntos de intersección, en nuestro espacio tridimensional.

Como estamos hablando de nudos en topología, esto significa que podemos deformar estirando o encogiendo la línea, es decir, la cuerda, y cambiándola de forma en el espacio, lo cual no altera el nudo, siempre que no se corte o pegue la misma. De hecho, se dice que dos nudos son equivalentes, que para nosotros es tanto como decir que “son iguales desde el punto de vista topológico”, cuando se puede deformar un nudo en el otro de forma continua, es decir, sin realizar cortes, ni pegar.

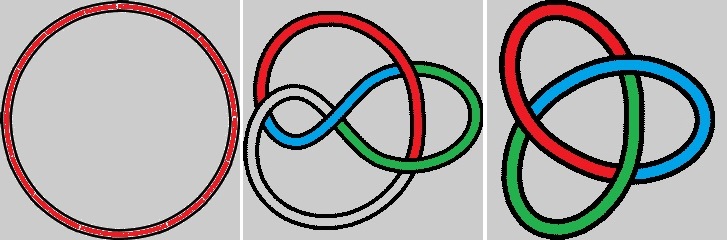
El nudo más simple es cuando cogemos la cuerda y unimos los extremos sin anudar, es decir, es la circunferencia, en la que no existe un nudo como tal, podríamos decir que es el no-nudo. Cualquier deformación espacial de la circunferencia, como en la imagen de abajo realizada con el juguete Tangle, sigue siendo el no-nudo.

El nudo más sencillo no trivial es el nudo de trébol, que es cuando hacemos un nudo sencillo a la cuerda y después anudamos los extremos. Es imposible deformarlo al nudo trivial sin cortar la cuerda y volver a pegarla, luego topológicamente el no-nudo y el nudo de trébol no son el mismo, no son equivalentes.

El nudo de trébol es un símbolo muy común desde la antigüedad, ya que su versión plana es la triqueta, o triquel, que fue ampliamente utilizada, por ejemplo, en el arte celta, en la religión cristina, como símbolo de la trinidad (padre, hijo y espíritu santo), en una de las versiones del Valnout alemán, que se relaciona con el dios Odín, o en el Mjolnir, martillo del dios Thor de la mitología nórdica. Y hoy en día nos la encontramos con mucha frecuencia en la cultura popular, por ejemplo, en la katana de Michonne de la serie de TV Walking Dead, así como en muchas otras series, películas o video juegos.

Para estudiar los nudos se utilizan representaciones gráficas planas de los mismos, que son proyecciones sobre el plano de los nudos tridimensionales, como si les hiciéramos una fotografía. Se utilizan solo las proyecciones buenas, las llamadas regulares, en las que solamente hay un número finito de puntos dobles (cruces) como puntos singulares. En las proyecciones no regulares perderíamos parte de la información del nudo. Estas representaciones se llaman diagramas del nudo. Son líneas continuas en el plano, que solo se pintan discontinuas cuando esa parte del nudo pasa por debajo de la que ya está pintada, como se muestra en los siguientes ejemplos. También podemos pensar en los diagramas de los nudos, como la representación de un nudo, como cuerda anudada, que apoyamos en una superficie plana.

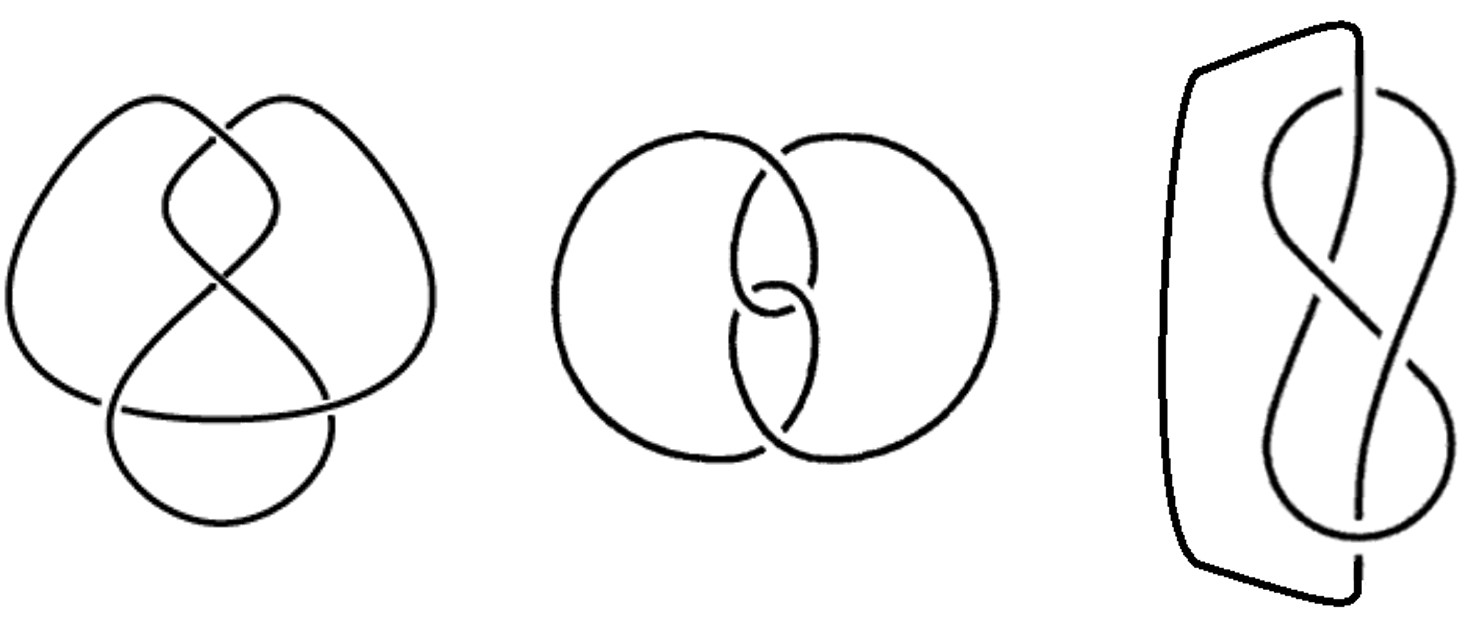
El nudo de Saboya, o nudo del ocho, que aparece en la anterior imagen, es un nudo cuyo diagrama tiene cuatro cruces, el diagrama del trébol tenía solamente tres, y se llama así porque aparece en el escudo de armas de la Casa de Saboya.

A continuación, mostramos el diagrama del nudo de la obra Sin título (1963), de Anni Albers.

La teoría de nudos estudia las propiedades topológicas de los nudos, en particular, el problema más importante es la clasificación de los diferentes nudos que existen, el cual incluye el problema de reconocimiento, es decir, determinar cuándo dos nudos son equivalentes, para lo cual se desarrollan herramientas matemáticas que nos permitan saber cuándo dos nudos son, o no, equivalentes (el mismo desde el punto de vista topológico).

En particular, deberemos de estudiar cuando dos diagramas corresponden a nudos equivalentes. Por ejemplo, nos podemos preguntar si un diagrama complejo como el que aparece en la imagen de abajo, y que se conoce como nudo gordiano de Haken, es topológicamente equivalente al no-nudo, es decir, que no hay nudo, solamente está enmarañado. El propio matemático alemán Wolfgang Haken, conocido por demostrar junto al matemático estadounidense Kenneth Appel el teorema de los cuatro colores, demostró que efectivamente dicho nudo es equivalente al no-nudo.

En la década de 1920, que fueron los inicios de la teoría de nudos, el matemático alemán Kurt Reidemeister (1893-1971), dio una primera herramienta para determinar cuándo dos diagramas correspondían a nudos equivalentes. Demostró que:

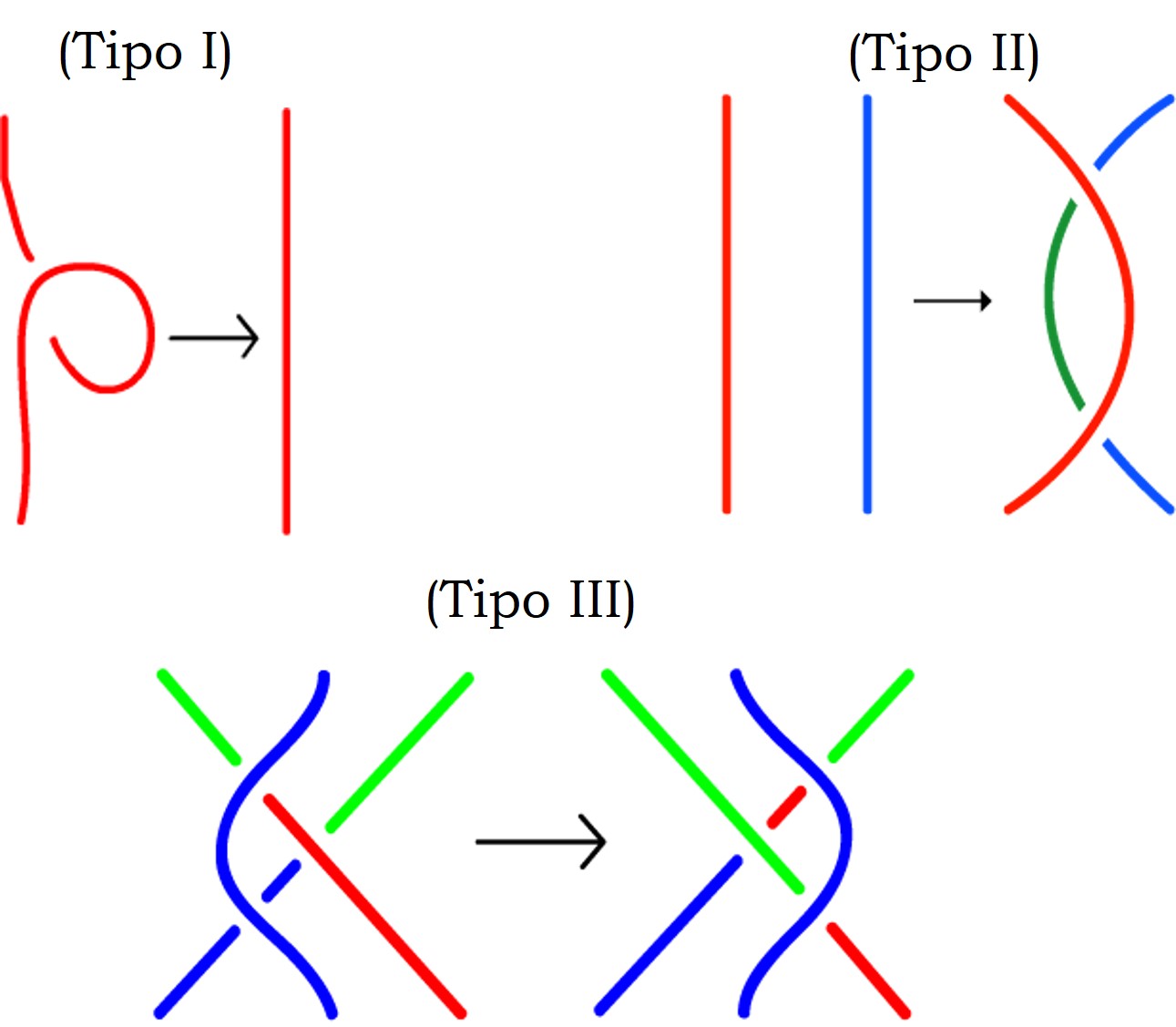
“Dos diagramas representan nudos equivalentes si, y sólo si, se puede pasar de uno a otro mediante un número finito de transformaciones del tipo I, II y III (que se muestran a continuación).”

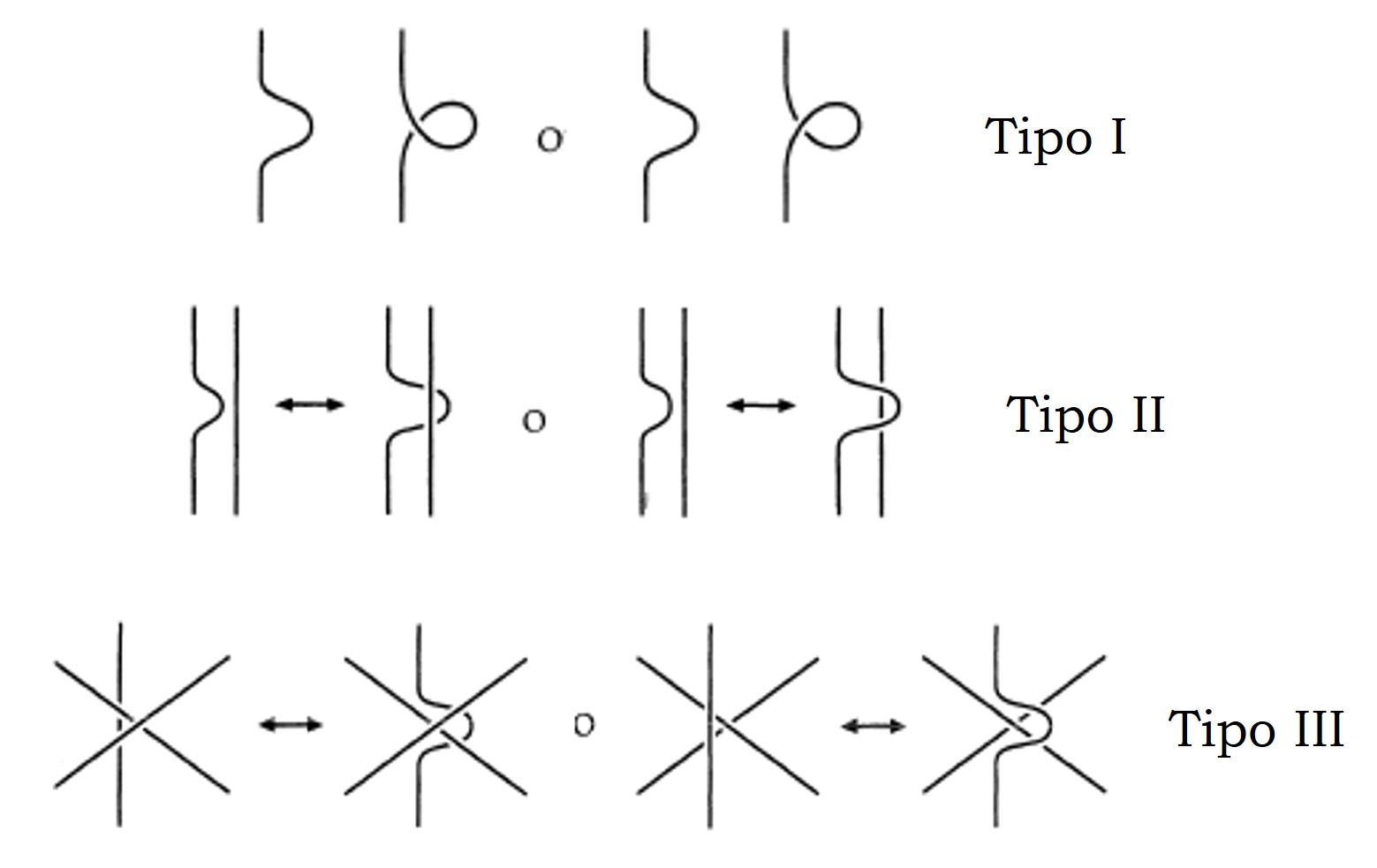
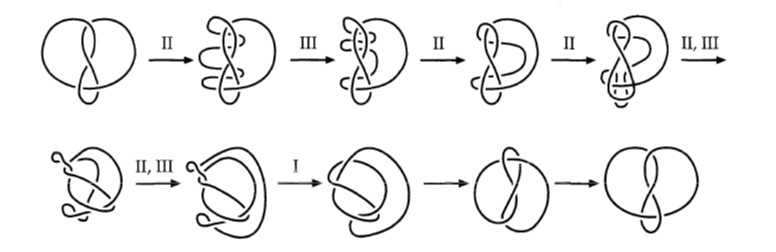
A continuación, vemos un nudo con tres cruces que es equivalente al nudo de trébol, puesto que mediante una serie de movimientos de Reidemeister puede transformarse uno en otro, como se muestra en la siguiente imagen.

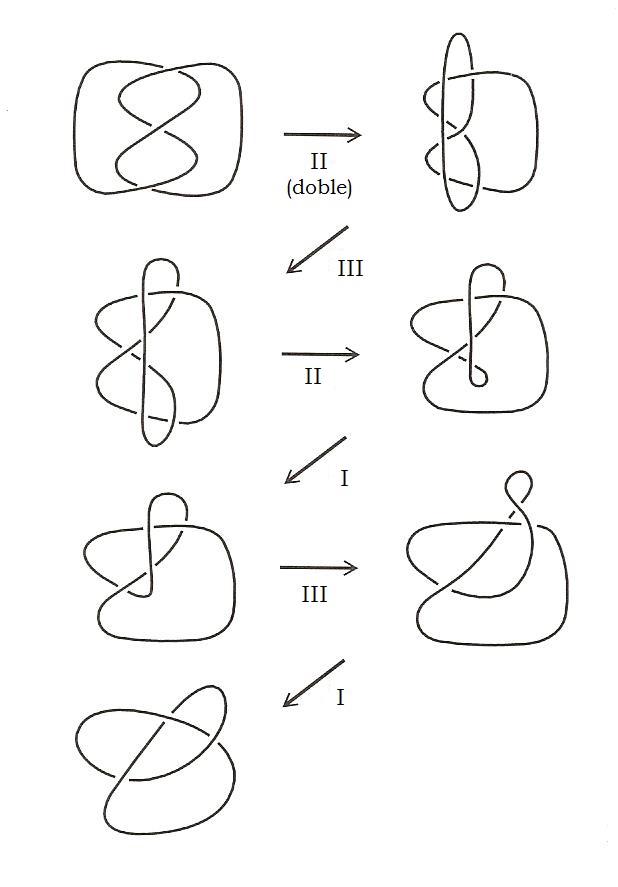
Existe un tipo especial de nudos, aquellos que son equivalentes a su imagen especular. Se llaman nudos anfiquirales. La imagen especular de un nudo es aquella que se obtiene como reflejo en un espejo, es decir, es el nudo simétrico respecto a un plano del espacio. Dado el diagrama de un nudo, entonces el diagrama del nudo imagen especular del primero es igual salvo que tiene los cruces dados la vuelta, es decir, la línea continua se convierte en discontinua, y la discontinua en continua.

El nudo de Saboya es un nudo anfiquiral, como se muestra en la siguiente imagen, mientras que el nudo de trébol puede demostrarse que no es anfiquiral.

Otra división importante de los nudos de cara a su estudio y clasificación es en nudos primos y nudos compuestos. La idea es descomponer los nudos en otros más simples, los llamados nudos primos, que son los que no se pueden descomponer en otros más simples aún y a partir de los cuales se generan todos los demás, y entonces centrar el estudio general de los nudos en estos.

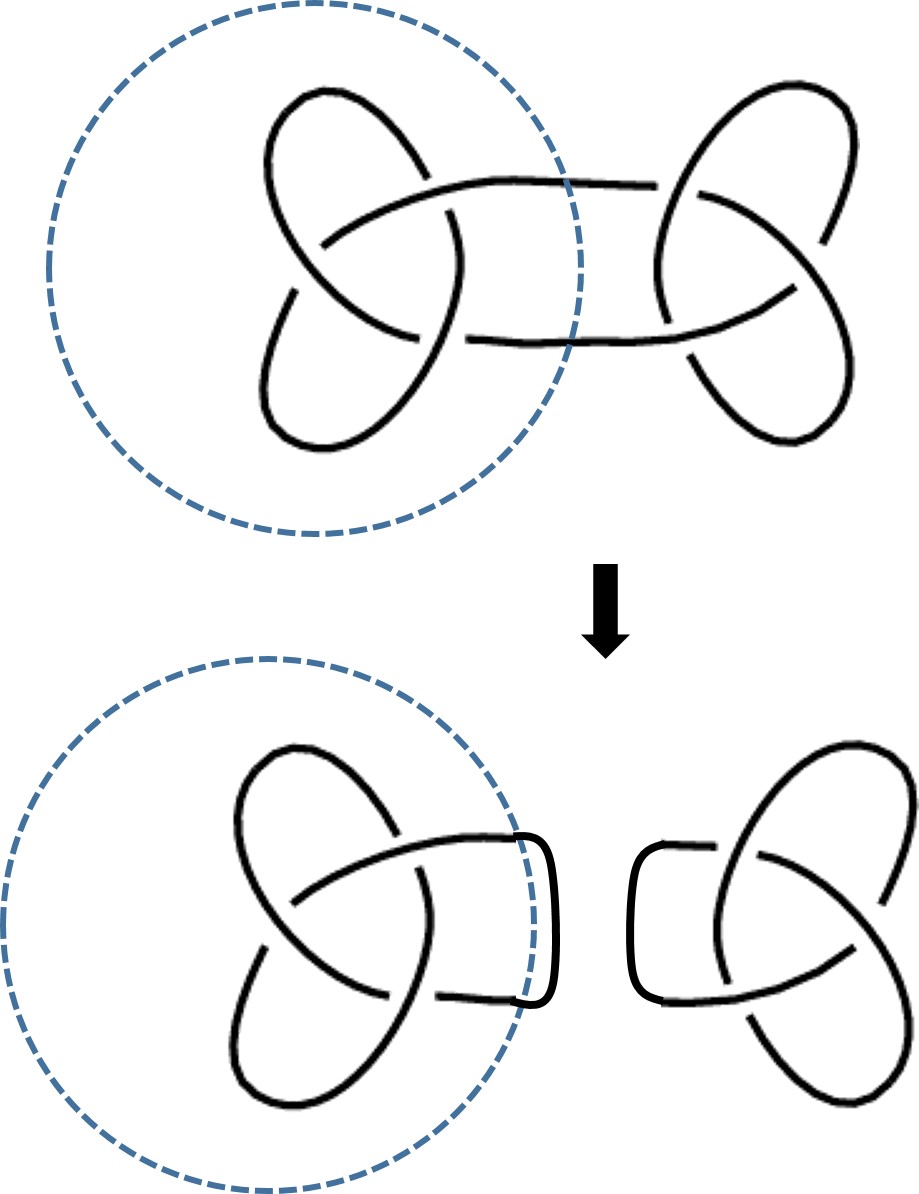
Por lo tanto, tenemos dos “operaciones” con nudos, que son una inversa de la otra, la descomposición y la suma conexa. Un nudo se descompone mediante una esfera (en el diagrama plano sería una circunferencia) que corta transversalmente al nudo en dos puntos, por los que se corta el nudo generándose dos partes disjuntas, cada una de las cuales se cierra de nuevo al pegar los dos puntos extremos mediante un segmento, generándose así dos nudos. Un nudo es primo si no se puede descomponer en dos nudos no triviales.

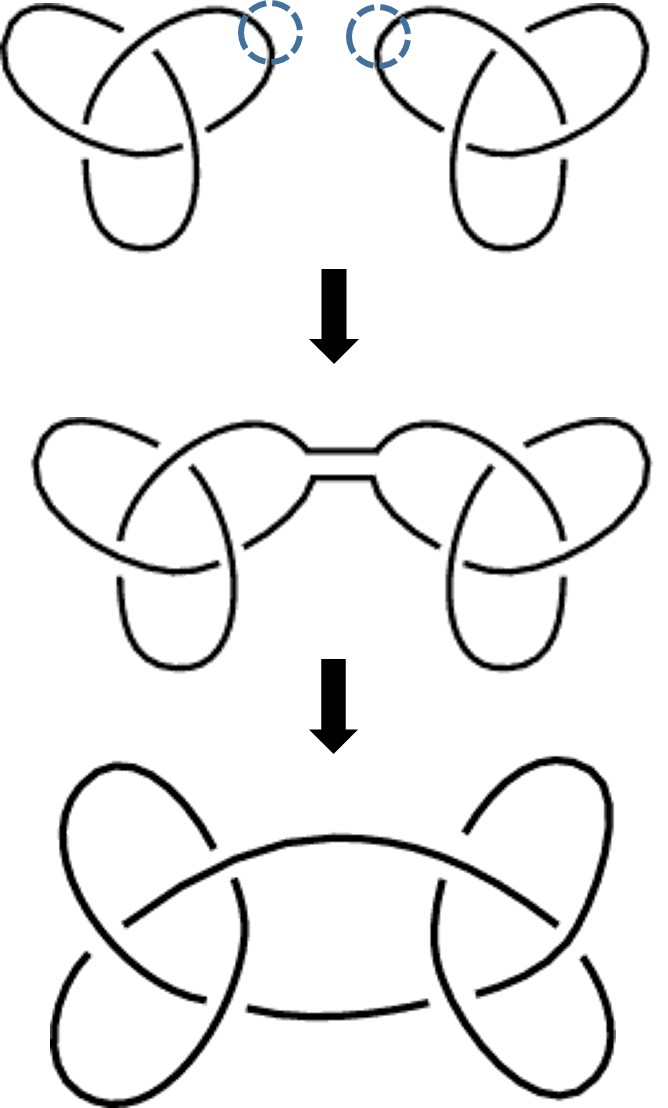
Cualquier nudo no primo se obtiene mediante la operación inversa a la anterior, la suma conexa, a partir de un número finito de nudos primos. En la imagen siguiente vemos la suma conexa del nudo de trébol y de su imagen especular, que es el nudo de rizo o nudo cuadrado.

El nudo de la abuela, que es la suma conexa de dos copias del nudo de trébol, es un nudo no anfiquiral, mientras que el nudo de rizo, que es la suma conexa del nudo de trébol y su imagen especular, sí es anfiquiral. En consecuencia, ambos nudos no son equivalentes.

Algunos de los nombres de los nudos matemáticos, como el nudo del ocho, el nudo de la abuela, el nudo de rizo, el nudo del cirujano o el nudo del amor verdadero, entre otros, derivan de los nombres de los nudos físicos, los nudos utilizados en la navegación y en muchas otras actividades de nuestra sociedad, como la escalada, la medicina, la costura o la decoración, desde la antigüedad.

Según el diccionario de la RAE, un nudo (físico) es un “lazo que se estrecha y cierra de modo que con dificultad se pueda soltar por sí solo, y que cuanto más se tira de cualquiera de los dos cabos, más se aprieta”. En matemáticas, para estudiar cómo de anudado está un nudo se unen los dos cabos del mismo, cerrando el nudo y no dejando que se pueda deshacer.

Pero continuemos con el estudio topológico de los nudos. Con el fin de resolver el problema de la clasificación de los nudos se introducen invariantes de los mismos. Los invariantes son objetos (por ejemplo, un número, un polinomio o un grupo) o propiedades (como la tricoloreabilidad) de un nudo, que tienen el mismo valor para todos los nudos equivalentes. En consecuencia, si un invariante es distinto para dos nudos, estos no pueden ser equivalentes.

Un primer ejemplo de invariante sería el “mínimo número de cruces de un nudo”. Consideremos un nudo N, se define el mínimo número de cruces c(N) del nudo N, como el menor número de cruces que puede tener un diagrama D de N, es decir, si denotamos por c(D) el número de cruces de un diagrama D, sería el mínimo valor de c(D), para todos los diagramas D del nudo N.

Si c(N) = 0, entonces N es el nudo trivial. No existen nudos para los cuales el mínimo número de cruces sea 1 o 2, cualquier diagrama que dibujemos con 1 o 2 cruces se puede transformar mediante movimientos de Reidemeister en el no-nudo. Los únicos nudos con c(N) = 3 son el nudo de trébol, y su imagen especular, mientras que el único con c(N) = 4 es el nudo de Saboya.

La primera clasificación de los nudos la realizó el matemático inglés Peter G. Tait en 1846, sin las herramientas aún de la topología, e incluía todos los nudos primos con mínimo número de cruces menor o igual que 7, que son el no-nudo y los 14 que aparecen en la imagen de abajo (obsérvese que en dicha clasificación no se está distinguiendo entre un nudo y su imagen especular).

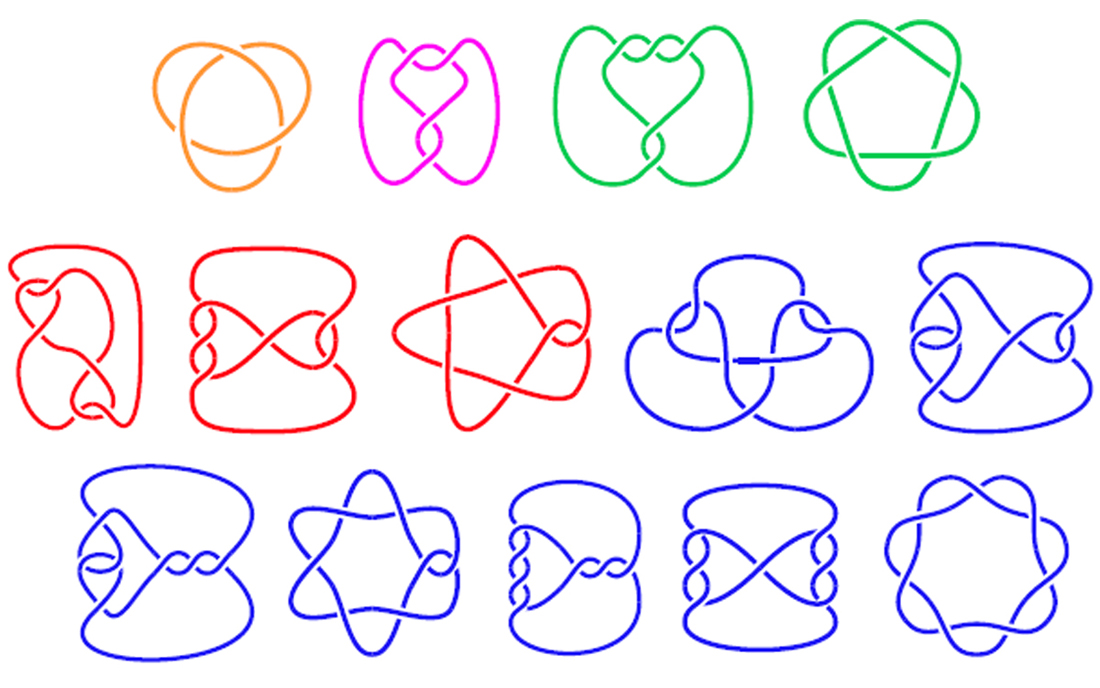
Un invariante sencillo, que nos permitirá distinguir entre algunos nudos que no son equivalentes, es la tricoloreabilidad. Un diagrama se dice que es tricoloreable si, dado un conjunto de tres colores, se puede asignar un color a cada arco del diagrama de forma que: i) se utilizan al menos dos de los tres colores; ii) si en un cruce aparecen dos de los colores, entonces también aparece el tercero.

Se puede demostrar fácilmente que la coloreabilidad no varía con los tres tipos de movimientos de Reidemeister, por lo que, si un diagrama es tricoloreable, lo es cualquier otro equivalente. Es decir, si un diagrama es tricoloreable y otro no, entonces se corresponden con nudos no equivalentes.

El no-nudo es trivialmente no tricoloreable, ya que no se puede utilizar más de un color, el nudo de trébol sí es tricoloreable y el nudo de Saboya no.

Veamos un ejemplo de cómo distinguir nudos, con el mismo número mínimo de cruces, mediante la tricoloreabilidad. Los nudos 7₁ y 7₄, que podemos ver en la clasificación anterior (el primero y cuarto de los nudos con mínimo número de cruces 7), y que tienen mínimo número de cruces, no son equivalentes, ya que 7₁ no es tricoloreable, mientras que 7₄ sí lo es.

Claramente el nudo 7₁ no es tricoloreable, puesto que, si pintamos uno de los segmentos de un color, por ejemplo, rojo, solo pueden ocurrir dos cosas, o todos los demás son también rojos, con lo cual no se utilizan al menos dos colores, o los colores de los demás segmentos quedan determinados y al llegar de nuevo al segmento rojo inicial habrá tres cruces cada uno con dos colores y por cada color elegido para el segmento que falta por marcar se obtienen dos cruces con solo dos colores, como se muestra en la siguiente imagen.

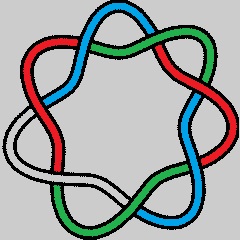
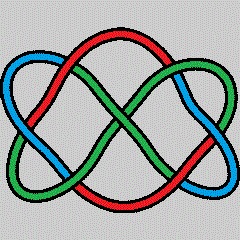
Mientras que el nudo 7₄, que es un nudo celta y también el nudo infinito del Budismo, es tricoloreable, como se muestra en la siguiente imagen.

Continuará en mi siguiente entrega de la sección Matemoción del Cuaderno de Cultura Científica…

…CONTINUARÁ…

Bibliografía

1.- Museo Guggenheim-Bilbao, Anni Albers, tocar la vista, 6 de octubre de 2017 – 14 de enero de 2018.[]

2.- The Josef and Anni Albers Foundation

3.- Canal de youtube del Museo Guggenheim-Bilbao, Anni Albers, Tocar el viento.

4.- Raúl Ibáñez, La topología modifica la trayectoria de los peces, Cuaderno de Cultura Científica, 2016.

5.- María Teresa Lozano, La teoría de nudos en el siglo XX, Un Paseo por la Geometría 1998/99, Departamento de Matemáticas, UPV/EHU, 1999. Versión on-line en divulgamat

6.- Sergio Ardanza Trevijano, Excursiones matemáticas en biología, Un Paseo por la Geometría 2005/06, Departamento de Matemáticas, UPV/EHU, 2006. Versión on-line en divulgamat

7.- Martín Gardner, Huevos, nudos y otras mistificaciones matemáticas, Gedisa, 2002.

8.- Colin C. Adams, The Knot Book, An Elementary Introduction to the Mathematical Theory of Knots, AMS, 2001.

9.- Stephan C. Carlson, Topology of Surfaces, Knots, and Manifolds, John Wiley and Sons, 2001.

10.- The Knot Atlas

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica