El número π es una de las constantes matemáticas más importantes que existen, pero además es un número fascinante que goza de una gran popularidad entre el público, matemático y no matemático. Por este motivo, el 14 de marzo, es decir, 3/14 en inglés (o también en euskera), se celebra el internacional Día de pi, debido a la sencilla aproximación a π que nos enseñaron en la escuela, 3,14.
El día de pi se celebra desde el año 1988 a partir de la idea propuesta por el físico Larry Shaw, y apoyado por el hecho de coincidir con la fecha del cumpleaños de Albert Einstein. También es el aniversario del nacimiento de un gran matemático, el polaco Wlaclaw Sierpinski (1882-1969), aunque prácticamente desconocido fuera de las matemáticas, salvo por los fractales que llevan su nombre.
Este año la Cátedra de Cultura Científica, junto con BCAM (Basque Center for Applied Mathematics) y Naukas, se han querido sumar a la celebración internacional del Día de Pi, y hemos organizado la jornada BCAM-NAUKAS: Día de Pi. Toda la información sobre la misma la podéis encontrar aquí.
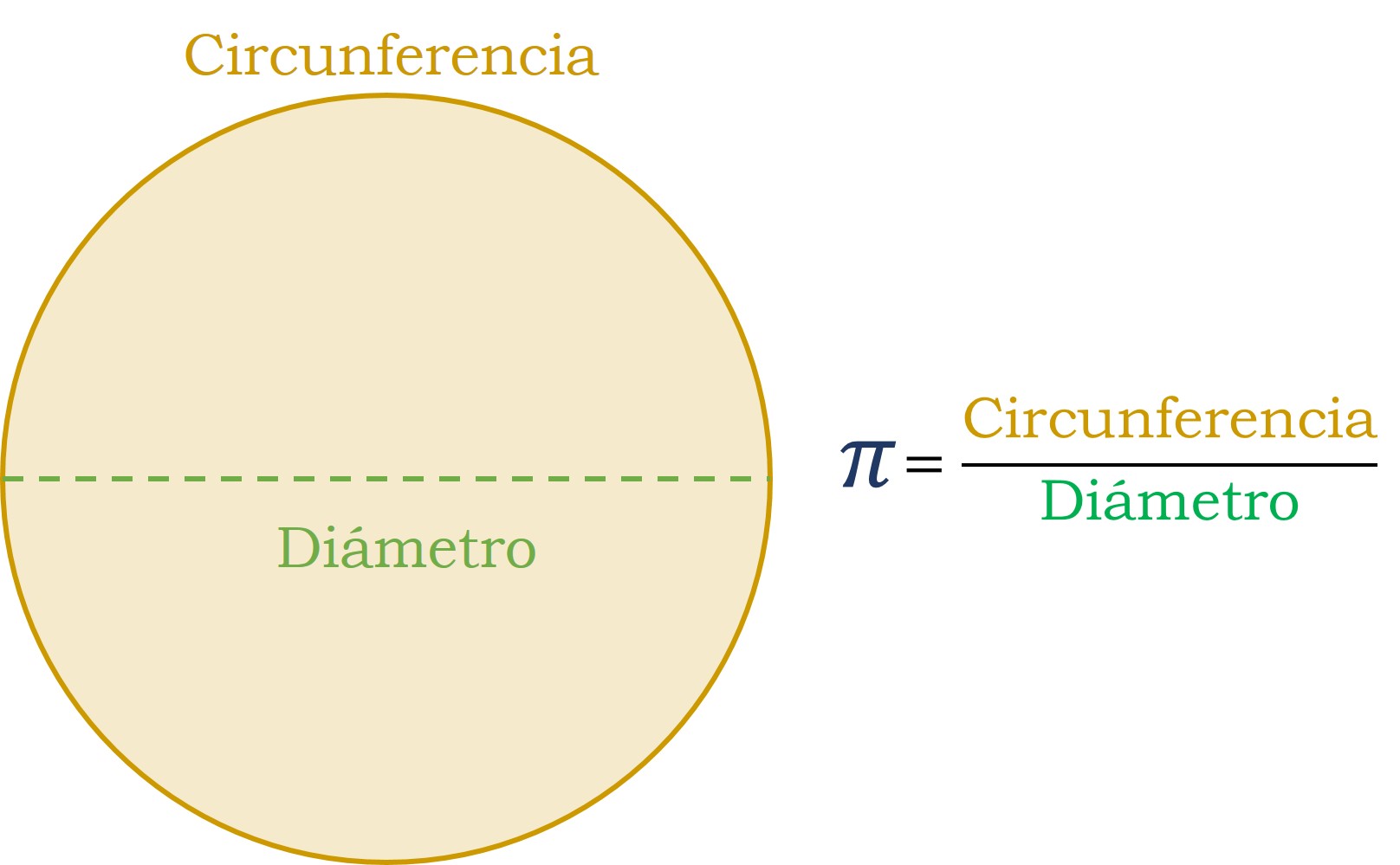
El número π, es decir, la relación entre la longitud de una circunferencia y su diámetro, tiene unos 4.000 años de edad. Desde la antigüedad se han intentado calcular aproximaciones suyas. En la Biblia se le daba el sencillo valor de 3 y en la actualidad, gracias a los ordenadores, se conocen más de 20 billones de sus infinitos decimales.
En uno de los más antiguos textos matemáticos, el Papiro de Rhind (1.700 años antes de nuestra era), el escriba Ahmés incluye la evaluación de un círculo inscrito en un cuadrado, que luego transforma en un octógono. A partir de ahí, el valor que propone para π, hecha la conversión, es (16/9)^2=3,16049…
En el 120 de nuestra era, el matemático chino Chang Hing llegará a la relación 142/45, es decir, 3,1555….
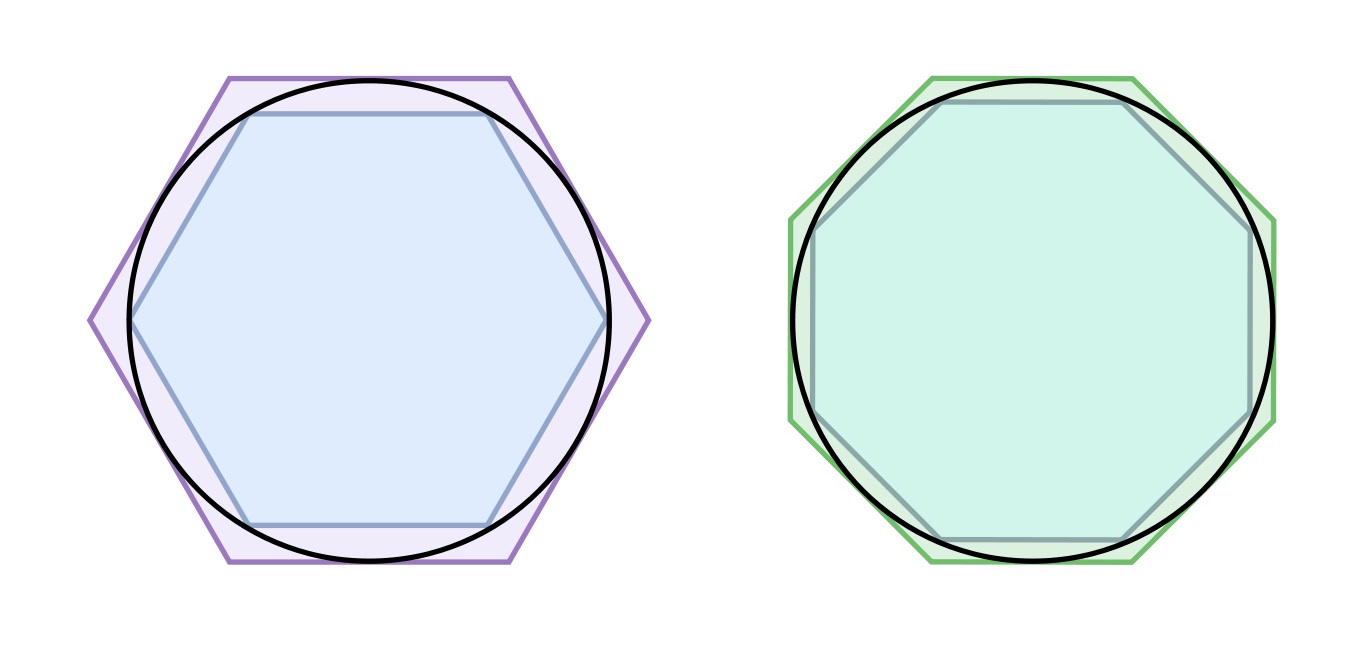
Arquímedes, en el siglo III a. C. se había acercado a la relación entre la circunferencia y el diámetro (π) no a través de una fracción sino como una sucesión de marcos (es decir, de diferentes pares de números cercanos, uno mayor y otro menor), que acotaban el valor de π. La idea era la siguiente… si se consideran las dimensiones de los cuadrados dibujados dentro y fuera del círculo y que tocan a su circunferencia, resulta obvio que πdebe ser mayor que 2 y menor que 4 (que es una aproximación muy burda)… a continuación podemos considerar hexágonos dibujados dentro y fuera del círculo y que tocan a su circunferencia, obteniendo así un nuevo marco para π …podemos seguir con octógonos…y Arquímedes llegó hasta utilizar polígonos de 96 lados, lo cual establecía que π está entre las cantidades 3+10/71 y 3+1/7. Ahora bien 3+1/7 es el famoso 22/7 (=3,1428…), fracción bien conocida en la escuela antes de las calculadoras.
En la India, el matemático Aryabhatta, hacia el 500, propuso 62.832/20.000, que es la aproximación cuyos cuatro primeros decimales son la aproximación más conocida, entre el público general, del número pi, 3,1416….
Como podemos observar todas estas aproximaciones que aparecieron en la historia se produjeron con números racionales, es decir, que son el cociente de dos números enteros, pero ¿es π un número racional?.
Recordemos brevemente el concepto de número racional. Como acabamos de decir, un número racional es aquel que puede expresarse como cociente de dos números enteros. Por ejemplo, 0,5 es un número racional ya que puede expresarse como el cociente 1/2; ó 0,333… es racional ya que puede expresarse como 1/3. Si consideramos la expresión decimal de los números (por ejemplo, 5,235), entonces un número es racional si podemos encontrar un “patrón entre sus decimales”, es decir, si los decimales del número son una cantidad finita (por ejemplo, 1/4=0,25) o si los decimales satisfacen que a partir de uno de los decimales se repite una pauta, un número finito de decimales que se repite de forma infinita, conocida como el período del número racional (por ejemplo, 1/3=0,333…, en el que se repite de forma infinita el 3; o 51/7=7,285714285714285714…, cuyo período es 285714). En la época de los pitagóricos se demostró, no sin cierta crisis existencial, que la raíz de 2 es un número no racional, que no puede expresarse como cociente de dos números enteros.
El número π tampoco es racional. No se puede expresar como cociente de dos números enteros, o lo que es equivalente, su expresión decimal es infinita y no hay un grupo de decimales que se repita de forma periódica generando todos los decimales. La primera demostración de que π es irracional se debe al matemático J. H. Lambert (1761).
De hecho, la búsqueda de los decimales del número π es una investigación activa hoy en día. Se trata de conocer todos los decimales posibles de π (recordemos que todos es imposible, son infinitos y no hay un patrón que se repita). El record de decimales en la actualidad es de … 22.459.157.718.361 dígitos … obtenido por Peter Trueb en 2016. Se tardaron 105 días en calcularlo y 28 horas en verificarlo.
El símbolo π viene de la palabra griega “periferia” περιφέρεια y fue utilizado por primera vez por el matemático inglés William Oughtred en 1652.
3,14159265358979323846264338327950288419716939937510582097494459230781640
6286208998628034825342117067982148086513282306647093844609550582231725359
4081284811174502841027019385211055596446229489549303819644288109756659334
4612847564823378678316527120190914564856692346034861045432664821339360726
0249141273724587006606315588174881520920962829254091715364367892590360011
33053054882046652138414695…
Parte de la magia de este número es que aparece en los lugares más insospechados, y tiene infinidad de aplicaciones, aunque como muchas otras constantes matemáticas. En todas las ramas de las matemáticas, desde la geometría hasta la probabilidad, pasando por la teoría de números, en física (en el principio de incertidumbre de Heisenberg, la teoría de la relatividad o la ley de Coulomb de la electricidad), en geología (para estimar la longitud de los ríos, debido a que relaciona dicha longitud con la distancia directa del nacimiento del río a su desembocadura), en bioquímica (en el estudio de la estructura de una molécula de ADN), en astronomía (en la búsqueda de exo-planetas o el estudio de la forma del universo), y muchas aplicaciones más en navegación, análisis de señales, dinámica de poblaciones o ingeniería, incluso en deportes (para calcular las posiciones de salida en las pistas de una carrera de atletismo, como vimos en la entrada Pi atleta).
Debido a la fascinación que existe por el número pi nos lo encontramos ampliamente en la cultura, del cine a la literatura, de la música a las series de animación, de las artes plásticas al humor gráfico, incluso la revista Investigación y Ciencia lo utilizó, este pasado 2017, para una broma del día de los inocentes, Las leyes cuánticas cambian el valor de pi.
El poema Número pi de la Premio Nobel de literatura, la polaca Wislawa Szymborska (1923-2012), empieza así “El número Pi es digno de admiración//tres coma uno cuatro uno//todas sus cifras siguientes también son iniciales//cinco nueve dos, porque nunca se termina.//No permite abarcarlo con la mirada seis cinco tres cinco//con un cálculo ocho nueve//con la imaginación siete nueve//o en broma tres dos tres, es decir, por comparación//cuatro seis con cualquier otra cosa//dos seis cuatro tres en el mundo”.
La cantante inglesa Kate Bush, en su disco Aerial (2005), tiene una canción dedicada al número π. En la película La cortina rasgada de Alfred Hitchcock, el símbolo π era el nombre de una organización secreta de la resistencia en la República Democrática Alemana durante la Guerra Fría. El número πtiene un papel protagonista en la película de Darren Aronofski, Pi, fé en el caos (2000). En la novela, y también en la película, La vida de pi (2001), del escritor Yann Martel, el apodo del protagonista es “Pi” y tiene que ver con nuestro apasionante número.
En la famosa serie Los Simpson, cuyo contenido matemático en muy conocido (véase el libro Los Simpson y las matemáticas), también se menciona el número π en más de una ocasión. Por ejemplo, uno de los personajes secundarios de la serie, es el tendero hindú Apu, quien tiene una gran capacidad para el cálculo. En un capítulo en el que llevan a juicio a Marge, al olvidarse de pagar una botella en el supermercado, Apu es el principal testigo, y para demostrar su memoria dice que es capaz de recitar 40.000 decimales del número π. Y dice que “el último decimal es el 1”.
De hecho, el record en memorización de los decimales del número pi está en 100.000 decimales, conseguido por el japonés Akira Haraguchi, en 2006. Necesitó 16 horas y 30 minutos para recitar, de memoria, todos estos decimales. El método que utiliza para recordar los decimales es asociar cada cifra, de 0 a 9, con una sílaba. Por ejemplo, el cero se asocia con alguna de las siguientes, ra, ri, ru, re, ro, wo, on or oh, e igual con el resto. Aunque este record no ha sido reconocido oficialmente por el Libro Guinness de los Records. Por lo tanto, el record oficial está en la memorización de 70.000 decimales, conseguido por el indio Rajveer Meena en 2015.
Otra referencia graciosa a π en Los Simpson, es cuando Lisa le habla a su padre del número π y Homer se pone a babear ya que en inglés tarta (pie) y π se pronuncian igual, “pai”.
En la serie hermana de la anterior, Futurama, también hay varias referencias al número π. Una lata de aceite lubricante -en-1(parodiando la frase 3-en-1), la -th Avenue después de la 3rd Avenue, la marca de muebles y complementos del hogar Kea, o el concurso televisivo «¿Cuál es el último dígito de ?«.
Hay muchísimas referencias a nuestro amado número, pero me gustaría dedicar lo que nos queda de esta entrada para hablar de una propiedad matemática de este número (aunque aún no se ha conseguido demostrar) y la expresión artística de esta propiedad que realiza la artista donostiarra Esther Ferrer.
Como hemos comentado más arriba, el número π no es racional, es decir, su expresión decimal contiene infinitos decimales, pero que no poseen un patrón que se repita (no es un decimal periódico). Aunque podríamos plantearnos cuales de las diez cifras básicas 0, 1, 2, …, 9 aparece con más frecuencia, y cuales, con menos, dentro de la expresión decimal del número π, o si por el contrario todas las cifras aparecen en la misma proporción.
Si miramos a los 100 primeros decimales del número π,
3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679…
observaremos que las diez cifras básicas aparecen en la siguiente proporción:
Si las diez cifras básicas aparecieran en la misma proporción, tendrían que aparecer diez veces cada cifra básica en los 100 primeros números, aunque la verdad es que 100 decimales no son muchos, y necesitaríamos ver más decimales. ¿Qué ocurre para 1.000, 10.000, 100.000, o más, decimales?
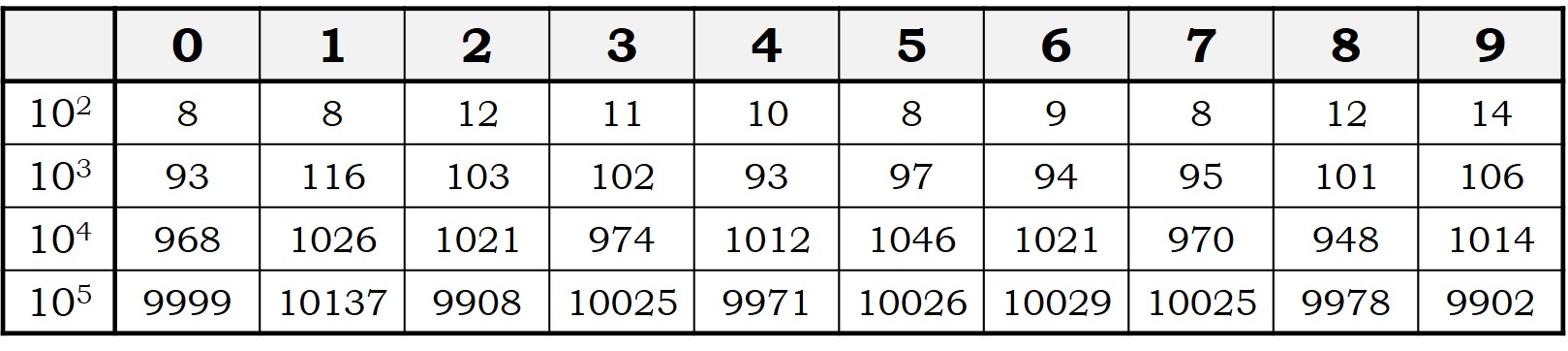
Como podemos observar, según va aumentando el número de decimales, la proporción de cada una de las diez cifras básicas dentro de los decimales del número π se van acercando a 1/10, es decir, al 10% de los decimales.
En el artículo Digit Statistics of the First 22.4 Trillion Decimal Digits of Pi, su autor, Peter Trueb, nos confirma este hecho entre los 22.459.157.718.361 decimales que se han calculado del número π. Más aún, si se toman las 100 secuencias de dos dígitos formadas por las diez cifras básicas, del 00 al 99, cada una aparece en una proporción que se va acercando cada vez más a 1/100, es decir, un 1%. Y lo mismo ocurre para las 1.000 secuencias de tres dígitos, de 000 a 999, cada una de las cuales aparece en una proporción que se va aproximando a 1/1.000. Todas las secuencias posibles son igualmente probables.
Todo esto lo que nos está diciendo es que aparentemente el número π podría ser lo que se conoce como un número normal (para la base 10). El concepto de número normal fue introducido por el matemático francés Émile Borel (1871-1956) en 1909. La definición es la siguiente:
Un número real x es normal para la base b (por ejemplo, 2 para los números binarios o 10 para la representación decimal usual) si los infinitos dígitos de la representación del número x en la base b están distribuidos de una forma uniforme, es decir, las b cifras básicas (por ejemplo, 0 y 1 en la representación binaria, o 0, 1, 2, …, 9 en la representación decimal) tienen la misma “densidad natural”, es decir, según vamos aumentando el número de decimales su proporción, para todos la misma, se aproxima a 1/b, todos los posibles pares, b2, de dígitos formados por dos cifras básicas tienen la misma densidad natural 1/b2, todos los triples , b3, de dígitos formados por tres cifras básicas tienen la misma densidad natural 1/b3, etcétera.
Los números racionales (por ejemplo, el número 51/7 = 7,285714285714285714… cuyo período es 285714) son, en general, no normales para la base 10 (o cualquier base), puesto que sus decimales son finitos o una expresión finita que se repite de forma infinita (por ejemplo, las cifras básicas 0, 3, 6 y 9 no aparecen en el desarrollo infinito de 51/7, mientras que las cifras 1, 2, 4, 5, 7 y 8 aparecen con una densidad normal de 1/6). Y podemos generar números irracionales que sean no normales si, por ejemplo, los construimos de forma que en su expresión decimal no haya una cierta cifra básica, por ejemplo, el 3.
El conocido como número de Champernowne, es decir,
0,12345678910111213141516171819202122232425…
es, por construcción, normal en base 10, pero podría no serlo para otras bases. De hecho, un número x se dice que es normal (aunque algunas personas lo denominan absolutamente normal) si x es normal para cualquier base b.
Émile Borel demostró que casi todos (en un sentido matemático que no abordaremos aquí) los números son normales, aunque existen infinitos (no numerables) números no normales.
Pero volviendo a nuestro popular número π, aparentemente, o al menos, así lo da a entender el comportamiento de los 22.459.157.718.361 decimales que se han calculado del número π, este podría ser un número normal para la base 10. Sin embargo, a día de hoy aún no existe una demostración matemática de este hecho.
La artista donostiarra Esther Ferrer, de la que ya hablamos en la entrada Variaciones artísticas del teorema de Napoleón, ilustra esta propiedad en su obra Pi (2009-2010), que pudo verse en la exposición Esther Ferrer. En cuatro movimientos (Artium, 2011-2012).
La obra Pi (2009-2010), de Esther Ferrer, consta de 21 lienzos, que podemos ver en la imagen de arriba. En la pared de la derecha hay un lienzo separado del resto, que sería como el lienzo inicial, y luego cada lienzo de la izquierda se corresponde con uno de la derecha, y con una cifra básica, que protagoniza esa pareja de lienzos.
En cada lienzo están representados los primeros decimales del número pi (junto al 3 entero inicial) hasta un cierto número. La artista realiza una cuadrícula muy grande, de 79 × 79 = 6.241 cuadraditos, en los cuales va a representar el número entero 3 inicial y los 6.240 primeros decimales de π. Cada cuadrado va a estar pintado de un color en función de la cifra básica que esté en dicho cuadrado, es decir, a lo largo de todo el lienzo cada cifra básica se corresponde con un color (0 amarillo, 1 azul claro, 2 morado, 3 rojo, 4 verde oscuro, 5 rosa, 6 verde claro, 7 naranja oscuro, 8 azul oscuro, 9 naranja claro). Además, los dígitos del número π se empiezan a pintar en el centro y recorriendo los cuadrados en espiral, 3,141592…
Como cada color está relacionado con una cifra básica, de 0 a 9, entonces la obra Pi (2009-2010) tiene como objetivo transmitir de un vistazo, a través de los colores, cual es la proporción y la distribución (en espiral) de las cifras básicas entre los primeros decimales de π.
Con el objetivo de visualizar el comportamiento de cada una de las cifras en particular, cada uno de los diez lienzos que estaban en la pared de la izquierda, solamente incluían el color de una cifra básica. El primer lienzo solo los cuadraditos amarillos, en los que se encuentra la cifra 0, en el segundo lienzo solo los cuadraditos de color azul claro que se corresponden con el número 1, y así con el resto. Mientras que, en frente de cada uno de los lienzos, estaba el lienzo complementario, es decir, estaban pintados todos los cuadraditos con su color correspondiente, salvo el de la cifra que le tocaba, así en el primer lienzo todos los colores salvo el amarillo del 0, en el segundo lienzo todos menos el azul claro del 1, y así para el resto.
Precisamente, este lunes 12 de marzo, a las 19:00, en el Biblioteca de Bidebarrieta (Bilbao), tendremos la oportunidad de conversar sobre la utilización de las matemáticas en los procesos creativos de la artista Esther Ferrer y el compositor Tom Johnson, dentro del programa Diálogos en la frontera (de Bidebarrieta Científica).
Bibliografía
1.- Celebra el día de Pi con BCAM Naukas en Bilbao, Cuaderno de Cultura Científica, febrero 2018.
2.- Alfred S. Posamentier, Ingmar Lehmann, La proporción tracendental. La historia de π, el número más misterioso del mundo, Ariel, 2006.
3.- Simon Singh, Los Simpson y las matemáticas, Ariel, 2013.
4.- Peter Trueb, Digit Statistics of the First 22.4 Trillion Decimal Digits of Pi, 2016. Preprint Arxiv 1612.00489
5.- Esther Ferrer, Catálogo de la exposición Esther Ferrer. En cuatro movimientos, Artium. Centro Museo Vasco de Arte Contemporáneo, Acción Cultural Española (AC/E), 2011. Publicación on-line.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
René Aga
Una demostración de que las matemáticas no son exactas (dixit Albert Einstein) Son una aproximación a la realidad. No solo en la religión existe el infinito?
Manitu69
Muy interesante el articulo pero como todo en ciencia casi me surgen mas preguntas de las que el articulo contesta.
Por ejemplo:
Si nadie a calculado el numero pi completo (es infinito) como sabemos que realmente no hay fin?
Podría ser que el final de pi fuese el momento en el que la relación de los 10 dígitos (base 10) fuese 10% exacta para todos ellos?
El numero pi se considera infinito siempre y cuando trabajemos en base 10, se ha intentado calcular el numero pi en diferentes bases para ver la relación entre ellos?
Y muchas mas.
Gracias por hacerme pensar un poquito mas de lo habitual.
Saludos
Raúl Ibáñez
Hola, muchas gracias por escribir.
La verdad es que sí se ha demostrado que existen infinitos decimales del número pi, y que no son periódicos, esa es precisamente la demostración de que pi no es racional, que realizó el matemático francés J.H. Lambert. Pero una cosa es saber que son infinitos y otra muy distinta saber cuales son.
Un fuerte abrazo, Raúl.
Javier
Un poquito tarde pero bueno…
Pi sería racional (y entero) si trabajamos en base pi, o múltiplo de pi; en otra situación, sería irracional y por tanto tomaría valores infinitos.
Y además, te cuento, si la geometría es la «normal» (la plana de los ejes XY de toda la vida de secundaria) pi es constante y toma el valor que conocemos. En el caso de que en esa geometría haya alguna curvatura, deja de ser constante.
Saludos
Javier
«Pi sería racional (y entero) si trabajamos en base pi, o múltiplo de pi; en otra situación, sería irracional y por tanto tomaría valores infinitos.»
Aquí tengo una incorrección por andar corriendo, además de que está pobremente explicado; allá voy: si la base es múltiplo de pi entonces pi es una razón de la base, ejemplo: base 2pi, implica que pi es igual a 1/2 (base 2pi) ya que 2pi es equivalente a 1 (en base 2pi). Se puede generalizar a cualquiera, por ejemplo 3pi es equivalente a 1 (en base 3pi) implica que pi es igual a 1/3 /base 3pi).
En general y más simple, si la base es un múltiplo de pi (k·pi) entonces pi será una fracción de esa base que corresponde con el número en base 10 (si 2pi es 1 pi es 1/2…)
Después de todo esto ya queda claro que si la base es pi, entonces pi es equivalente a 1 (base pi); entonces ya es no solo racional, sino que además es entero.
Javier
Perdón pero como no se puede editar y soy muy despistado, además de que no quiero dejar nada sin explicar.
Si la base es un divisor de pi como por ejemplo 1/2(pi) entonces pi que es el doble, sera 2 en esa base.
Ya está.
Manitu69
Muchas gracias Raúl y Javier, creo que mas o menos lo he entendido. Es creo fascinante, tengo la duda, siempre he escuchado que no existe la circunferencia perfecta (por lo menos en nuestro universo), que no podríamos acercar muchísimo pero siempre habría una pequeña diferencia, es esto debido a que el numero Pi es irracional?
Javier
En parte sí, pero no es la única razón.
Como pi es irracional, y pi=p (perímetro)/ d (diámetro); por las propiedades de los irracionales: o «p» o «d» (o ambos), tienen que ser racionales. Si ambos fueran racionales no hay forma de que se obtenga un número irracional. Entonces claro, representar gráficamente un número irracional es imposible en el sentido de que tiene infinitas cifras que «añaden» longitud a las anteriores. De hecho, a partir de la circunferencia goniométrica (de radio 1)
Pero la razón más importante de que no se pueda crear físicamente una circunferencia es simplemente que así es la realidad, la precisión necesaria para ello es imposible; evidentemente para nosotros no había diferencia.
Esto es el debate sobre la existencia de los «objetos matemáticos», si existen o son constructos humanos. Los objetos matemáticos realmente son objetos idílicos, que no existen físicamente pero que tienen «sentido».
Javier
DIOS… Debería repasar antes de publicar.
«por las propiedades de los irracionales: o «p» o «d» o ambos, tienen que ser IRRACIONALES.
Lo que iba diciendo que me corté: «De hecho, a partir de la circunferencia goniométrica (de radio 1)…» está muy claro: 2pi/2·1=pi.
Aún así, el tema de los irracionales es realmente irrelevante. Es cierto que partiendo de una base (por ejemplo la 10), representar en la recta numérica con exactitud, por ejemplo sqrt(2) (raíz cuadrada de dos) es imposible. Pero no importa por el hecho de que en cualquiera de las infinitas posibilidades de bases no enteras e incluso irracionales (véase: https://en.wikipedia.org/wiki/Non-standard_positional_numeral_systems), incluso 2, que es entero, sería irracional y por tanto irrepresentable. Usamos bases enteras naturales porque es lo lógico dado que es el sistema básico para contar, pero no dejan de ser elecciones matemáticamente arbitrarias.
Así que la razón de fondo realmente es la imperfección de la irrealidad.
Carlos F
Error básico: Pi es irracional en cualquier base. El número NO ES SU REPRESENTACIÓN.
10 representa el numero diez en base diez y el numero dos en base dos. También representa a Pi en base Pi (y no 1 como esta dicho arriba). Si uso una base irracional puedo representar a un número irracional con una cantidad finita de símbolos, pero si en esa base quiero representar el simple numero dos… tendrás que usar infinitos caracteres.
Francis
Raúl, tu afirmación «el número πtiene un papel protagonista en la película de Darren Aronofski, «Pi, fé en el caos» (2000)» deja claro que no has visto la película «Pi, fé en el caos» (1998), ya que π aparece de forma marginal en la trama (el maestro del protagonista trabaja en la normalidad de pi)… El gran protagonista de la película es la razón aúrea y su papel en la teoría de las ondas de Elliott https://es.wikipedia.org/wiki/Teor%C3%ADa_de_las_Ondas_de_Elliott . Pero en el título del film se consideró más comercial pi que tau (razón aúrea).
Raúl Ibáñez
Querido Francis,
Como siempre, tienes razón. Aunque sí he visto la película, fue hace mucho tiempo, y en mi cabeza se mezclan varias imágenes de la misma (la espiral aurea, pi, phi, la cábala, etc), en particular, imágenes en las que el protagonista busca patrones dentro de un número «irracional», que pensaba (en mi recuerdo) que era pi.
Gracias por la aclaración, aprovecharé para volver a ver la película 🙂
Un abrazo, Raúl.
Curro
Ojo, no se conocen 20 billones de dígitos. Hay un error de tres órdenes de magnitud.
Raúl Ibáñez
Hola,
Gracias por escribir.
Se conocen 22.459.157.718.361 decimales del número pi. Eso en el sistema europeo son 22 billones, y 22 trillones en el americano…
Un abrazo, Raúl.
Enrique
Me llama la atención que no se mencione una sencilla fracción aproximativa de PI con los tres primeros números impares: 355/113 (o, lo que es lo mismo (113/355)^-1) que es exacta hasta el sexto decimal
Joan
Buen artículo. Pero a mi entender el número de Champernowne no seria normal, puesto q tiene más unos q doses, más doses q treses, etc. Hay un teorema o principio sobre esto, q se utiliza para detectar entradas falsas en contabilidad etc. Me equivoco?
Juan Carlos Sacristán
Hola.
Gracias por el excelente artículo.
Tal como yo lo recuerdo, el nombre del protagonista de “La vida de Pi”, de Yann Martel, no tiene relación con el número Pi sino que es la abreviatura de su nombre: Piscina Molitor Patel.
Tal como cuenta el libro, un tío suyo, fanático de la natación, le puso al recién nacido el nombre de su piscina favorita en la que adoraba nadar: la Piscina Molitor de Paris. Patel es el apellido.
Y claro, le llamaban Pi para abreviar.
Saludos cordiales.
JC Sacristán
Raúl Ibáñez
Sí, pero esto es lo que cuenta después sobre su nombre…
«Después de San José, fui al Petit Séminaire, la mejor escuela secundaria de habla inglesa en Pondicherry. Ravi llevaba algunos años allí, e igual que todos los hermanos pequeños, me tocó sufrir el intento de seguirle los pasos a un hermano mayor muy popular. Fue el atleta de su generación en el Petit Séminaire, un lanzador temido y un bateador poderoso, el capitán del mejor equipo de criquet de la ciudad, nuestro preciado Kapil Dev. El hecho de que yo supiera nadar no produjo grandes olas, ni mucho menos. Parece ser que la gente que vive al lado del mar no se fía de los nadadores, igual que la gente de montaña no se fía de los alpinistas. Pero mi plan no era vivir eclipsado por nadie, aunque hubiera preferido cualquier nombre antes que «Pissing», aunque fuera «el hermano de Ravi». Tenía una idea mucho más brillante.
La llevé a cabo desde el primer día, desde la primera clase. Estaba rodeado por otros alumnos de San José. La clase empezó como suelen empezar todas las clases nuevas, es decir, con los nombres. Los dijimos en voz alta desde los pupitres, según el orden en que nos habíamos sentado.
—Ganapathy Kumar—dijo Ganapathy Kumar.
—Vipin Nath—dijo Vipin Nath.
—Shamshool Hudha—dijo Shamshool Hudha.
—Peter Dharmaraj—dijo Peter Dharmaraj.
Cada nombre se ganó una cruz en la lista y una mirada breve y mnemotécnica del profesor. Yo tenía los nervios de punta.
—Ajith Giadson—dijo Ajith Giadson, a cuatro pupitres…
—Sampath Saroja—dijo Sampath Saroja, a tres…
—Stanley Kumar
—Stanley Kumar, a dos…
—Sylvester Naveen—dijo Sylvester Naveen, el chico que tenía justo delante.
Me tocaba a mí. Había llegado la hora de deshacerme de Satán. Medina, allá voy.
Me levanté del pupitre y me dirigí rápidamente a la pizarra. Antes de que el profesor pudiera abrir la boca, cogí un trozo de tiza y dije, mientras escribía: Me llamo Piscine Molitor Patel, conocido por todos como (subrayé las dos primeras letras de mi nombre de pila) Pi Patel. Por si acaso, agregué:
Pi = 3,1416. Luego dibujé un círculo enorme y lo partí con un diámetro, para evocar aquella lección básica de geometría.
Hubo un silencio sepulcral. El profesor tenía los ojos clavados en la pizarra. Yo me estaba aguantando la respiración. Entonces dijo: —Muy bien, Pi. Siéntate. La próxima vez procura pedir permiso antes de levantarte del pupitre.
—Sí, señor. Me puso una cruz al lado del nombre y miró al chico siguiente. —Mansoor Ahamad—dijo Mansoor Ahamad. Me había salvado. —Gautham Selvaraj—dijo Gautham Selvaraj. Podía respirar tranquilo. —Arun Annaji—dijo Arun Annaji. Borrón y cuenta nueva. Repetí el mismo espectáculo con todos los profesores. La repetición es un factor esencial, no sólo para adiestrar a los animales, sino también a los humanos. Entre un chico de nombre corriente y el siguiente, salía disparado a la pizarra y estampaba en ella (en más de una ocasión con un chirrido estrepitoso) los detalles de mi renacimiento. Mis compañeros no tardaron en corear conmigo, un crescendo que acababa en clímax, tras una inhalación brusca mientras subrayaba la nota pertinente, haciendo una interpretación tan conmovedora de mi nuevo nombre que hubiera hecho delicias de cualquier director de coro. Algunos de mis compañeros susurraban con urgencia: «¡Tres! ¡Coma! ¡Catorce! ¡Dieciséis!», mientras yo escribía a toda prisa. Al final partía el círculo con tanto ímpetu que salían volando trocitos de tiza.
Ese mismo día, cada vez que levanté la mano aprovechando cualquier excusa, los profesores me concedieron la palabra con una sola sílaba que me sonaba a música celestial. Los alumnos siguieron su ejemplo. Incluso los diablos de San José. Es más, mi nombre se puso de moda. Sin lugar a dudas, somos una nación de ingenieros que aspiran a ser reconocidos: poco después, un chico llamado Omprakash se apodó Omega, otro que se hizo llamar Épsilon, y hubo una temporada en que teníamos un Gamma, un Lambda y un Delta. Pero yo fui el primero y el más perdurable de los griegos en el Petit Seminaire.»
7. Bibliografía – El numero π
[…] Ibáñez, R. (2018, 7 marzo). ¿Es normal el número pi? Recuperado 4 octubre, 2018, de https://culturacientifica.com/2018/03/07/normal-numero-pi/ […]
7. Bibliografía | El numero π
[…] Ibáñez, R. (2018, 7 marzo). ¿Es normal el número pi? Recuperado 4 octubre, 2018, de https://culturacientifica.com/2018/03/07/normal-numero-pi/ […]
Legislar sobre una verdad matemática — Cuaderno de Cultura Científica
[…] la entrada ¿Es normal el número pi? ya hablamos del número pi, de los diferentes intentos históricos de aproximar esta constante […]
BCAM-Naukas 2023: Fotografía con lente matemática — Cuaderno de Cultura Científica
[…] sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que […]
BCAM-Naukas 2023: Un paseo por el firmamento, de mano de la geometría — Cuaderno de Cultura Científica
[…] sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que […]
BCAM-Naukas 2023: ¿Pueden las máquinas cambiar de opinión a lo largo del tiempo? — Cuaderno de Cultura Científica
[…] sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que […]
BCAM-Naukas 2023: Defendiendo a Newton — Cuaderno de Cultura Científica
[…] sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que […]
BCAM-Naukas 2023: Cómo calcular el número π a hostias — Cuaderno de Cultura Científica
[…] sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que […]
BCAM-Naukas 2023: Las sencillas matemáticas de nuestro universo — Cuaderno de Cultura Científica
[…] sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que […]
Día de pi 2024: La música de los números primos — Cuaderno de Cultura Científica
[…] número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e […]
Día de pi 2024: El tamaño importa… ¿o no? — Cuaderno de Cultura Científica
[…] número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e […]
Demostraciones visuales en dimensiones superiores
[…] número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e […]
Día de pi 2024: Viaje hacia la modelación de un NanoUniverso
[…] número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e […]
Matemáticas, flecha del tiempo y mentes
[…] número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e […]
Día de pi 2024: Soy de letras — Cuaderno de Cultura Científica
[…] número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e […]