Mientras escribía mi último libro Números primos, amigos y demás familia (Catarata, 2021), que estará en las librerías en abril, he descubierto números con propiedades muy curiosas e interesantes, entre ellos, la constante de Kaprekar.

El número 6.174 es aparentemente un número de lo más normal, un número de esos que no llamaría nuestra atención, sin embargo, posee una propiedad matemática que parece pura magia. En 1949 el matemático recreativo indio Dattatreya Ramchandra Kaprekar (1905–1986) publicó el artículo Another Solitaire Game, en la revista Scripta Mathematica, en el que describía las curiosas propiedades que había descubierto sobre el 6.174, aunque fue la publicación en la columna Mathematical Games de Martin Gardner en la revista Scientific American, lo que le daría un mayor reconocimiento.

Consideremos un número de cuatro dígitos cualquiera, tal que estos no sean todos iguales (por ejemplo, 6.282), con sus dígitos escribimos los números mayor y menor que se pueden representar, es decir, 8.622 y 2.268, y los restamos

8.622 – 2.268 = 6.354.

Ahora repetimos este proceso,

6.543 – 3.456 = 3.087.

Seguimos con el mismo proceso,

8.730 – 0378 = 8.352.

Este parece un proceso artificial en el que se irán generando números sin parar. Sin embargo, en el siguiente paso se alcanza el número 6.174, ya que

8.532 – 2.358 = 6.174.

Y nuestro número 6.174 es un número particular respecto a este proceso ya que este se estaciona y siempre queda 6.174.

7.641 – 1.467 = 6.174.

Al proceso descrito se le llama algoritmo de Kaprekar y lo sorprendente es que siempre –salvo para números con los cuatro dígitos iguales– se llega a la denominada constante de Kaprekar, el número 6.174. Veamos otro ejemplo. Si empezamos con el número de cuatro dígitos –recordemos que no todos iguales– 3.631, la sucesión de números que nos da el algoritmo de Kaprekar es

6.331 – 1.336 = 4.995;

9.954 – 4.599 = 5.355;

5.553 – 3.555 = 1.998;

9.981 – 1.899 = 8.082;

8.820 – 0288 = 8.532;

8.532 – 2.358 = 6.174;

donde se estaciona el proceso, ya que hemos llegado a la constante de Kaprekar. Mientras que en el primer ejemplo habíamos necesitado de cuatro pasos, en este han sido necesarios seis pasos.

Si todos los dígitos del número son iguales, como 7.777, entonces el algoritmo de Kaprekar se estaciona en el primer paso, llegando a cero, ya que el mayor y el menor número que se puede formar con esos dígitos es el mismo 7.777, y entonces 7.777 – 7.777 = 0.

Por lo anteriormente visto, sabemos que el número 6.174 es un punto fijo del algoritmo de Kaprekar, es decir, al aplicarlo a él mismo, nos vuelve a dar ese número: 7.641 – 1.467 = 6.174. Una de las cuestiones que nos podríamos haber planteado inicialmente es el cálculo de todos los puntos fijos que existen para ese algoritmo. Veamos, a continuación, una idea de la prueba de que realmente la constante de Kaprekar es el único punto fijo posible.

Sea un número de cuatro dígitos, no todos ellos iguales, entonces podemos expresar al mayor número que se puede representar con sus cuatro dígitos como abcd, donde 0 ≤ a ≤ b ≤ c ≤ d ≤ 9, y al menor como dcba, luego la resta de ambos será un número ABCD tal que

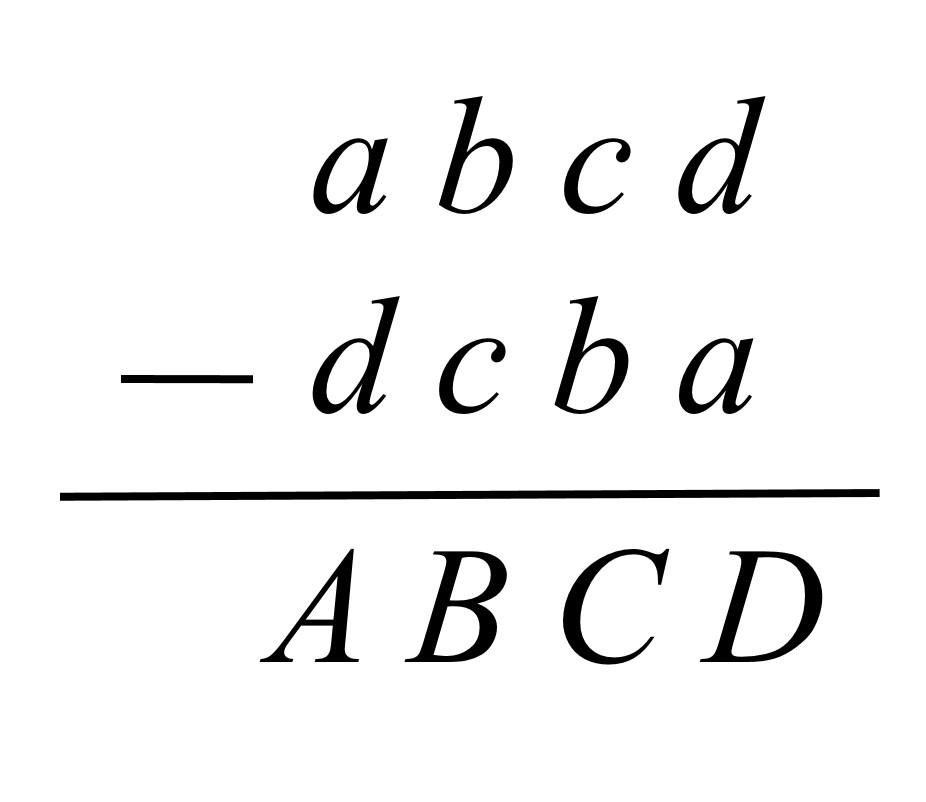
de donde se obtienen las siguientes relaciones:

D = 10 + d − a (a > d)

C = 10 + c − 1 − b = 9 + c − b (b > c − 1)

B = b − 1 − c (b > c)

A = a − d.

Como buscamos un punto fijo, sabemos que {A, B, C, D} = {a, b, c, d}, salvo el orden. Como existen 4! = 24 permutaciones (ordenes) posibles de {a, b, c, d}, si probamos todas ellas veremos que el anterior sistema con cuatro ecuaciones y cuatro incógnitas (a, b, c, d) tiene solución única solo cuando A = b, B = d, C = a, D = c. Además, en ese caso la solución única es precisamente a = 7, b = 6, c = 4 y d = 1.

La siguiente cuestión matemática sería demostrar esta propiedad mágica, es decir, que para cualquier número de cuatro dígitos, tal que estos no sean todos iguales, el algoritmo de Kaprekar llega siempre a la contante de Kaprekar, 6.174. Más aún, se puede probar que el número de pasos para llegar a la constante es como mucho siete. Para quien esté interesado en la demostración de esta propiedad puede consultarla en la literatura que existe sobre esta cuestión, por ejemplo, en el artículo The weirdness of number 6174, de Yutaka Nishiyama.

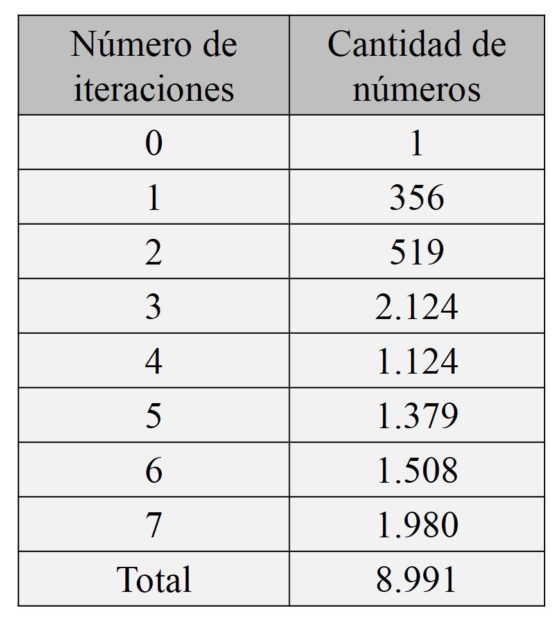
En los ejemplos que se han mostrado en esta entrada del Cuaderno de Cultura Científica, hemos visto que para el número 6.282 se necesitan 4 iteraciones del algoritmo de Kaprekar para llegar a la constante 6.174 y para el número 3.631 se necesitan 6 iteraciones. En el siguiente diagrama vemos la cantidad de números de cuatro dígitos, no todos ellos iguales, que necesitan una cantidad dada de iteraciones para alcanzar el 6.174.

Esta interesante propiedad descubierta por el matemático recreativo indio Dattatreya Ramchandra Kaprekar para números de cuatro dígitos la podríamos pensar para números con otras cantidades de dígitos.

Para números con dos dígitos veamos, para empezar, un ejemplo. Si tomamos el número 53 y realizamos el algoritmo de Kaprekar, la sucesión de números que aparecen es 18, 63, 27, 45, 09, 81 y se repetiría el ciclo 63, 27, 45, 09, 81 todo el tiempo. De hecho, esta situación es la general, para cualquier número de dos dígitos, tal que estos no sean todos iguales, el algoritmo de Kaprekar llega siempre al ciclo 63, 27, 45, 09, 81. Por lo tanto, no existe una contante de Kaprekar de dos dígitos.

Si tomamos un número de tres dígitos, como 184, entonces el algoritmo de Kaprekar da lugar a la sucesión 693, 594 y 495, siendo este último un punto fijo en el que se estaciona la sucesión. De hecho, para números de tres dígitos el número 495 es una constante de Kaprekar, la única para esta cantidad de dígitos.

No existe una constante de Kaprepkar para números de cinco dígitos. Para estos lo que ocurre es que el algoritmo de Kaprekar terminará en alguno de los ciclos siguientes:

Ciclo 1: 53.955, 59.994, 53.955;

Ciclo 2: 61.974, 82.962, 75.933, 63.954, 61.974;

Ciclo 3: 62.964, 71.973, 83.952, 74.943, 62.964.

Mientras que para seis dígitos tenemos una mezcla de las situaciones anteriores. Existen dos constantes de Kaprekar (549.945 y 631.764), es decir, puntos fijos del algoritmo de Kaprekar, a las que convergerán muchas de las sucesiones de números construidas mediante este algoritmo, y un ciclo (420.876, 851.742, 750.843, 840.852, 860.832, 862.632, 642.654, 420.876).

En la Enciclopedia on-line de sucesiones de números enteros (oeis.org [https://oeis.org/]), de N. J. A. Sloane, podéis encontrar la sucesión de constantes de Kaprekar. Es la sucesión etiquetada como A099009, cuyos primeros elementos son:

495, 6.174, 549.945, 631.764, 63.317.664, 97.508.421, 554.999.445, 864.197.532, 6.333.176.664, 9.753.086.421, 9.975.084.201, 86.431.976.532, 555.499.994.445, 633.331.766.664, 975.330.866.421, 997.530.864.201, 999.750.842.001, 8.643.319.766.532, 63.333.317.666.664, etc.

Bibliografía

1.- Raúl Ibáñez, Números primos, amigos y demás familia, Catarata, 2021.

2.- Martin Gardner, Los números mágicos del doctor Matrix, Gedisa, 2019.

3.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1986.

4.- Yutaka Nishiyama, The weirdness of number 6174, International Journal of Pure and Applied Mathematics, vol. 80, no. 3, pp. 363 – 373, 2012.

5.- Wikipedia: Kaprekar routine

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica