La entrada de hoy quiero dedicarla a una curiosa propiedad relacionada con el número 22. Este es un sencillo número de dos dígitos, que es par, capicúa y semi-primo, es decir, producto de dos primos, ya que es igual al producto de 2 y 11. Además, es un número pentagonal, como vimos en la entrada El asesinato de Pitágoras, historia y matemáticas (y II), un número heptagonal centrado (véase la entrada El problema de las flechas de Mahavira ) y el número de particiones del 8 (recordemos que una partición de un número entero positivo es una forma de expresarlo como suma de números enteros positivos, donde el orden no es relevante; por ejemplo, las particiones del número 3 son tres, a saber {1 + 1 + 1, 2 + 1, 3}, mientras que existen cinco particiones del número 4 {1 + 1 + 1 + 1, 2 + 1 + 1, 2 + 2, 3 + 1, 4}).

Pero vayamos con la curiosa propiedad del número protagonista de esta entrada, el número 22. Seguid mis instrucciones:

Selecciona un número de tres dígitos, con todos los dígitos diferentes entre sí, y escribe todos los números de dos dígitos posibles con esos tres dígitos (que serán seis). Entonces divide la suma de todos los números de dos dígitos obtenidos entre la suma de los dígitos del número original. ¿Qué ocurre?

Veamos qué ocurre con un ejemplo concreto. Sea el número de tres dígitos 739, que efectivamente tiene los tres dígitos diferentes. Los números de dos dígitos posibles con esos tres dígitos 3, 7 y 9 son 37, 39, 79, 73, 93 y 97. Sumamos estos números 37 + 39 + 79 + 73 + 93 + 97 = 418 y dividimos esta suma por la suma de los dígitos del número original 7 + 3 + 9 = 19, dando 418 / 19 = 22.

Como vemos el resultado es el número con el que habíamos empezado esta entrada, el 22. Pero esto puede ser casualidad. Por lo tanto, tomemos otro número, por ejemplo, 251, y veamos qué ocurre ahora. Para este número tenemos que 12 + 15 + 25 + 21 + 51 + 52 / 2 + 5 + 1 = 176 / 8 = 22. De nuevo, el número mencionado.

Da igual el número de tres dígitos que consideremos inicialmente, siempre vamos a obtener el mismo resultado, 22. Vamos a demostrar esta misteriosa propiedad.

Empecemos por un número de tres dígitos genérico abc, cuyo valor es: 100 a + 10 b + c. Tomemos los números de dos cifras que se pueden generar con ellos {ab, ac, bc, ba, ca, cb} y sumemos sus valores

(10 a + b) + (10 a + c) + (10 b + c) + (10 b + a) + (10 c + a) + (10 c + b),

que es igual a

10 (a + a + b + b + c + c) + (b + c + c + a + a + b) = 20 (a + b + c) + 2 (a + b + c),

que sacando factor común queda

22 (a + b + c),

que al dividirlo por la suma de los tres dígitos del número original a + b + c, queda claramente 22. Una vez más con un poco de algebra podemos demostrar un comportamiento misterioso de los números.

Este comportamiento misterioso relacionado con el número 22 nos permite realizar un sencillo truco de magia. Podemos escribir una predicción (que sería el número 22) en un papel y meterla en un sobre o dársela a alguna de las personas que están con nosotros, para luego pedir a alguna otra persona que elija un número de tres dígitos (todos ellos distintos) y siga las instrucciones que le explicamos (que son las escritas arriba). El resultado de sus operaciones coincidirá con nuestra predicción, el número 22.

Hemos pedido que los dígitos del número original sean distintos, sin embargo, por la demostración anterior vemos que el resultado sigue siendo válido cuando hay dígitos repetidos en el número de tres dígitos inicial, aunque los dos dígitos iguales hay que tratarlos como si fuesen diferentes. Por ejemplo, si tomamos el número 522, cuyos tres dígitos son 2, 2, 5, tenemos que los números de dos dígitos posibles con estos son 22, 25, 25, 22, 52 y 52, luego 22 + 25 + 25 + 22 + 52 + 52 / 5 + 2 + 2 = 198 / 9 = 22.

Vamos a terminar esta entrada del Cuaderno de Cultura Científica con algunas otras propiedades del número 22, además de las comentadas al principio de la entrada.

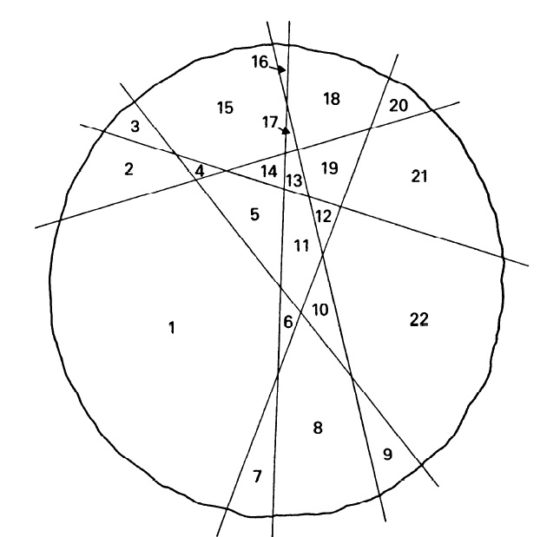
1. El número 22 es un número pancake, o número tortita, ya que la máxima cantidad de trozos de pancake, o tortita, que se pueden conseguir con 6 cortes es 22.

2. Los únicos números n para los cuales el factorial del número n! (véase la entrada Buscando lagunas de números primos [https://culturacientifica.com/2018/06/27/buscando-lagunas-de-numeros-no-primos/]) tiene n dígitos son 22, 23 y 24.

3. El 22 es un número cortés, o trapezoidal, ya que puede expresarse como suma de números naturales consecutivos, 22 = 4 + 5 + 6+ 7.

4. Es un número deficiente, ya que la suma de sus divisores propios es 1 + 2 + 11 = 14, menor que el propio número (véase la entrada Los números enamorados).

5. Es un número tal que el producto de sus dígitos 4 es igual a la suma de sus dígitos 4.

6. Su representación en la base binaria es 10110, por lo que se dice que es un número pernicioso, ya que la representación binaria contiene un número primo de unos (en este caso 3).

7. El número 22 es un número aritmético, ya que la media aritmética de sus divisores es un número entero 1 + 2 + 11 + 22 / 4 = 36 / 4 = 9. El número 24, por ejemplo, no es aritmético, ya que 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 / 8 = 60 / 8 = 7,5.

8. 22 es un número de Smith, ya que la suma de sus dígitos (2 + 2 = 4) es igual a la suma de los dígitos de sus factores primos, contados con multiplicidad (como 22 = 2 x 11, entonces 2 + 1 + 1 = 4). El número de la Bestia, 666, también es un número de Smith ya que 666 = 2 x 3 x 3 x 37 y 6 + 6 + 6 = 2 + 3 + 3 + 3 + 7.

Bibliografía

1.- Raúl Ibáñez, La gran familia de los números, Catarata, 2021.

2.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, Genios de las Matemáticas, RBA, 2017.

3.- Alfred S. Posamentier, Math Wonders to inspire Teachers and Students, ASCD, 2003.

4.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1986.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica