Los números capicúas, aquellos números tales que sus cifras leídas de izquierda a derecha y de derecha a izquierda son las mismas, llaman profundamente nuestra atención, hasta el punto que solemos buscarlos, e incluso coleccionarlos, en las matrículas de los coches, los décimos de lotería, los billetes de medios de transporte, los billetes de la moneda de cualquier país o cualquier otro lugar en el que aparezcan números de cuatro, o más dígitos. De la misma forma, cuando una fecha lleva asociada una expresión numérica capicúa nos parece una fecha curiosa y solemos prestarle atención, comentarlo e incluso darle cierta relevancia a la misma. Por este motivo, no he podido evitar empezar esta entrada del Cuaderno de Cultura Científica mencionando que ayer fue 22 de febrero de 2022, es decir, 22/02/2022, luego una fecha capicúa puesto que el número asociado a la misma, 22.022.022, es un número capicúa. Además, en esta fecha el número 22 tiene especial relevancia, ya que aparece tres veces el número 22, separado cada uno de los otros por un 0 (sobre el número 22 véase la entrada El misterioso número 22).
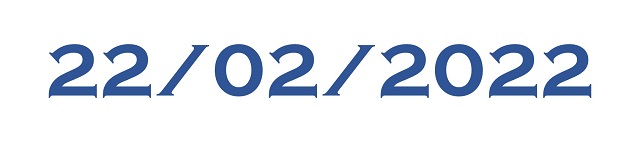
¿Qué pasa con el día de hoy, el 23/02/2022? Obviamente no es un número capicúa. Sin embargo, podemos obtener fácilmente un número capicúa a partir del mismo, con el simple proceso de sumarle el número simétrico, 23.022.022 + 22.022.032 = 45.044.054. Este es el algoritmo “invierte el orden y suma” del que hemos hablado en la entrada El secreto de los números que no querían ser simétricos (véase también el libro La gran familia de los números, Libros de la Catarata, 2021).
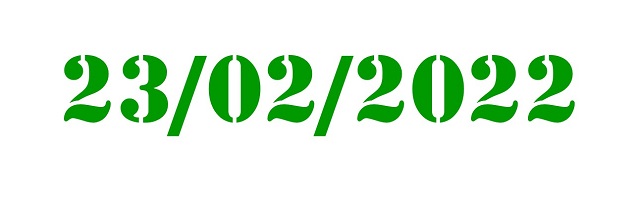
Pero, sigamos con el número asociado al día de hoy, 23.022.022 y pensemos qué propiedades numéricas tiene. Para empezar, este número se puede escribir como producto de tres números primos distintos, 23.022.022 = 2 x 79 x 145.709, es lo que se conoce en matemáticas con el nombre de “número esfénico”. Por lo tanto, tiene 8 divisores (incluyendo el 1 y él mismo: 1, 2, 79, 158, 145.709, 291.418, 11.511.011 y 23.022.022) y la suma de sus divisores propios es 11.948.378, que es una cantidad menor que nuestro número 23.022.022, luego este es un número deficiente (véase la entrada Los números enamorados o el libro La gran familia de los números). Además, es un “número aritmético” ya que, si se realiza la media aritmética de los divisores del número 23.022.022 el resultado es un número natural, en concreto, la media de los divisores de este número
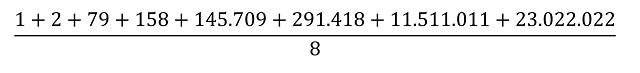
es 4.371.300.
Trivialmente, no es un número primo, ya que es par, pero tampoco es un número “potencialmente primo”, ya que no se puede obtener un número primo sin más que cambiar uno de sus dígitos (por ejemplo, el número 144 es “potencialmente primo” ya que si cambiamos su último dígito obtenemos un número primo, 149).
Más aún, 23.022.022 es un número trapezoidal, ya que puede expresarse como suma de dos, o más, números consecutivos, mayores que 1. Así, nuestro número puede expresarse como suma de los números consecutivos desde 72.697 hasta 73.012. Y se dice que 2 elevado a 23.022.022 es un número apocalíptico ya que incluye el número de la bestia, 666, entre sus dígitos.

Finalmente, el número que se corresponde con el día de hoy, 23.022.022, es un “número congruente”. Y este es el concepto que analizaremos brevemente en esta entrada.
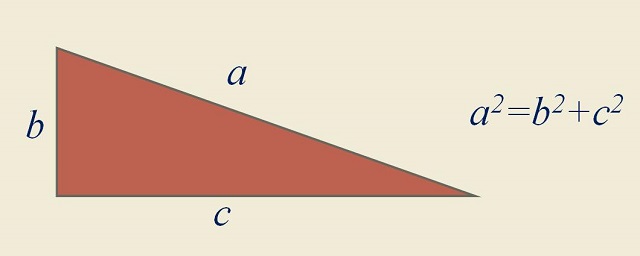
El concepto de número congruente está relacionado con el teorema de Pitágoras. Por lo tanto, como es nuestra costumbre, empecemos recordando este resultado geométrico: “dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos” (la famosa expresión a2 + b2 = c2, si a y b son los catetos y c la hipotenusa). De hecho, el teorema dice algo más, también es cierto el recíproco, es decir, que “dado un triángulo para el cual el cuadrado de uno de sus lados es igual a la suma de los cuadrados de los otros dos, entonces el triángulo es rectángulo”.
Por lo tanto, un número se llama congruente si es igual al área de un triángulo rectángulo cuyos lados, hipotenusa y catetos, son números racionales (recordemos que un número es racional si es el cociente a / b de dos números enteros a y b, como 0,5 = 1 / 2 ó 1,4 = 7 / 5). Por ejemplo, el triángulo egipcio, es decir, el triángulo rectángulo de lados (3, 4, 5), tiene área igual a 6, por lo tanto, el número 6 es un número congruente. Como puede verse en la siguiente imagen, los números 5, 6 y 7 son números congruentes (de hecho, los primeros).
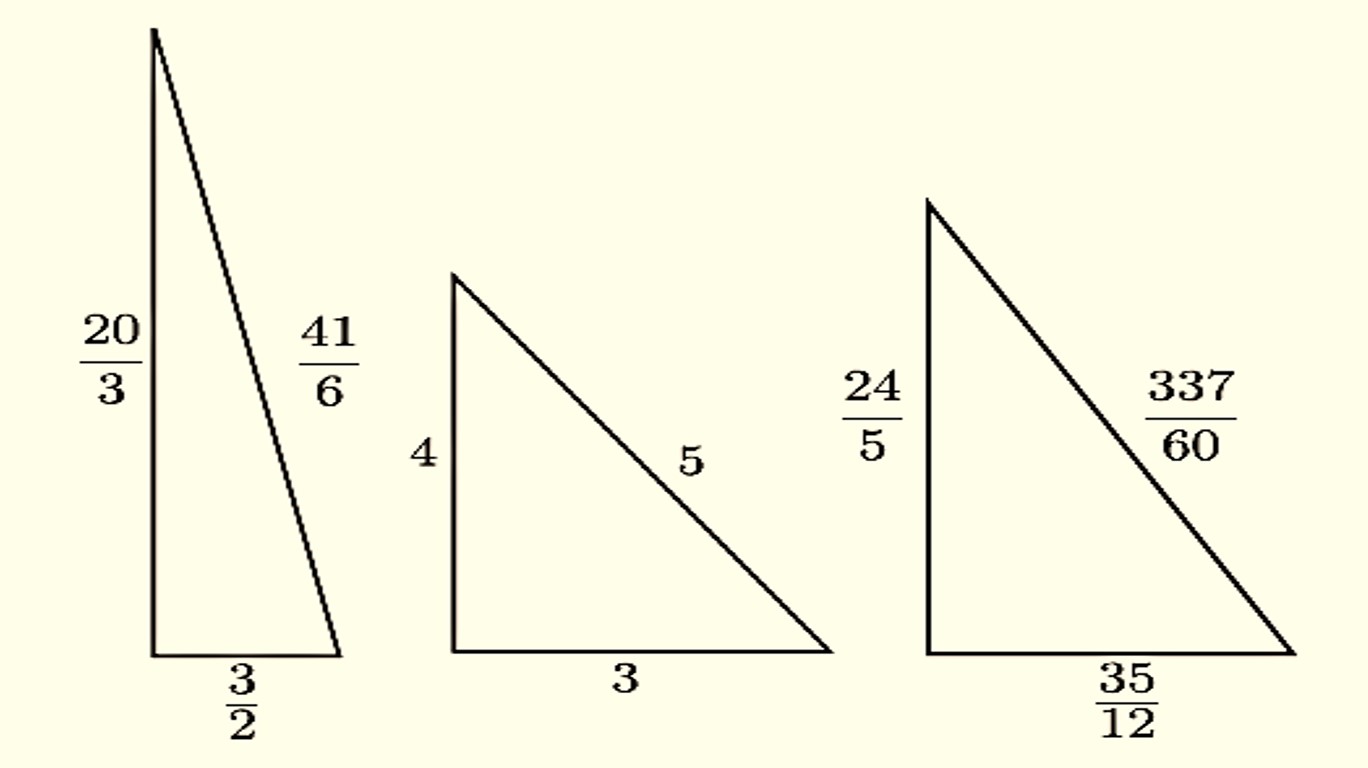
Como se indica en el libro History of the Theory of Numbers (volumen II), del matemático estadounidense Leonard Eugene Dickson (1874-1954), la historia de los números congruentes se inicia con el matemático griego Diofanto (siglo III). Aunque su estudio fue el tema central de dos manuscritos árabes del siglo X, en los que ya aparecen mencionados los números 5 y 6 como números congruentes. El matemático italiano Leonardo de Pisa (aprox. 1170-1240), conocido como Fibonacci, descubrió que el 7 también es un número congruente y afirmó, aunque sin demostrarlo, que el número 1 no es un número congruente, luego ningún número cuadrado lo es (ya que si m2 fuese un número congruente con triángulo rectángulo asociado (a, b, c), entonces 1 sería un número congruente con triángulo rectángulo asociado (a / m, b / m, c / m)). El matemático francés Pierre de Permat (1601-1665) fue el primero en demostrar que el número 1 no es un número congruente –y, por lo tanto, tampoco todos los números cuadrados-, ni tampoco los números 2 y 3.
Teorema (Fermat, 1640): El número 1 no es un número congruente.
La demostración de este resultado se realiza mediante la técnica del descenso infinito de Fermat. La idea es la siguiente. Para empezar, supongamos que existe un triángulo rectángulo, de lados racionales, cuya área sea igual a 1. Entonces renombrando los lados del triángulo rectángulo como a / d, b / d y c / d, con a, b, c y d números enteros, se tiene una 4-tupla de números enteros (a, b, c, d) tales que
![]()
A continuación, si tenemos una 4-tupla de números enteros (a, b, c, d) tales que satisfacen las ecuaciones (1), entonces puede demostrarse que a y b son coprimos (es decir, a no tienen divisores comunes, salvo el 1).
Entonces, el método del descenso infinito de Fermat consiste en demostrar que si tenemos una 4-tupla de números enteros (a, b, c, d) tales que satisfacen (1) y a y b son coprimos, puede construirse otra 4-tupla de números enteros (a’, b’, c’, d’) tales que satisfacen (1) y a’ y b’ son coprimos, con 0 < c’ < c (es decir, que el nuevo número c’ es más pequeño que c). Si seguimos realizando este proceso llegamos a una contradicción, puesto que es imposible realizar este proceso de forma infinita, ya que c es un número positivo (finito). Por lo tanto, no existe un triángulo rectángulo de lados racionales y área igual a 1.
Para quienes estén interesados en leer la demostración completa, y no solo este bosquejo, pueden consultar, por ejemplo, el artículo The Congruent Number Problem, del matemático Keith Conrad.

La sucesión de números congruentes está recogida en la Enciclopedia On-line de Sucesiones de Números Enteros (OEIS) como la sucesión A003273, cuyos primeros elementos son:
5, 6, 7, 13, 14, 15, 20, 21, 22, 23, 24, 28, 29, 30, 31, 34, 37, 38, 39, 41, 45, 46, 47, 52, 53, 54, 55, 56, 60, 61, 62, 63, 65, 69, 70, 71, 77, 78, 79, 80, 84, 85, 86, 87, 88, 92, 93, 94, 95, 96, 101, 102, 103, 109, 110, 111, 112, 116, 117, 118, 119, 120, …
Por otra parte, volviendo al concepto de número congruente, podemos observar que la condición de que un número N sea congruente es equivalente a que exista un número racional u tal que u2 – N y u2 + N son también cuadrados, que es como consideraron originalmente el problema Diofanto, los matemáticos árabes o Fibonacci. La justificación es sencilla. Si tenemos que N es un número congruente, entonces existen números racionales (a, b, c) tales que a2 + b2 = c2 y N = ab / 2, luego u = c / 2, ya que:
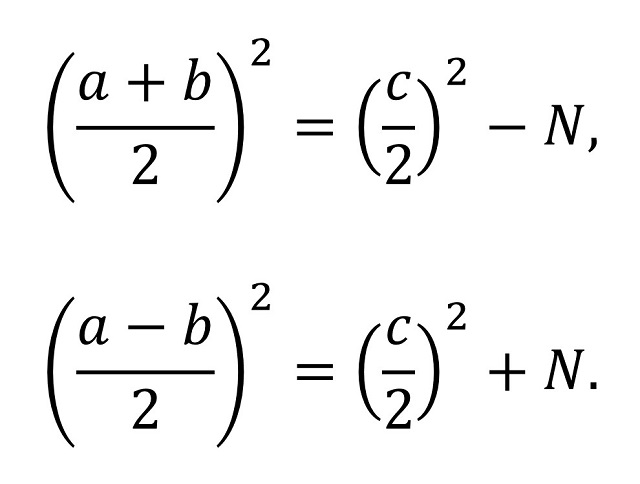
De forma análoga el recíproco. Es decir, estamos diciendo que la condición de que N sea un número congruente es equivalente a que existan números racionales u, p y q tales que
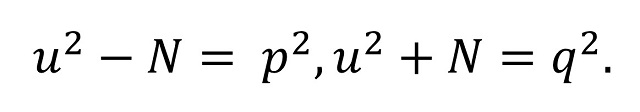
Teniendo en cuenta que u, p y q son racionales, luego cocientes de números enteros, se puede probar fácilmente que la condición de que un número N sea congruente es equivalente a que existan números enteros a, b, x, y tales que
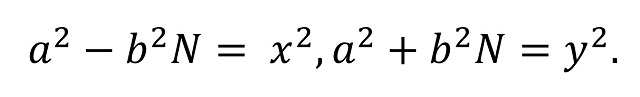

Obtener ejemplos de números congruentes no es difícil, basta con tener una terna o triple pitagórico, es decir, una terna de tres números enteros (a, b, c) que satisfacen la ecuación del teorema de Pitágoras a2 + b2 = c2, siendo uno de los números a o b par, ya que en ese caso el número N = ab / 2 es un número congruente.
Por ejemplo, si consideramos la fórmula de Euclides para generar ternas pitagóricas, es decir, dados dos números enteros n y m tales que m > n > 0, entonces
![]()
es una terna pitagórica y b siempre es par. En conclusión, a partir de este método se obtienen ejemplos de números congruentes.
Así, en la siguiente tabla podemos observar algunos ejemplos de ternas pitagóricas generadas con la fórmula de Euclides y el número congruente obtenido.

Existen otros métodos de generar ternas pitagóricas, aunque esto solo nos da algunos números congruentes, que además están generados mediante los lados enteros –no racionales en general- de un triángulo rectángulo.
Sin embargo, la cuestión importante, y más compleja, es conocer, dado un número entero cualquiera, si es, o no, un número congruente. Este es el conocido como el problema del número congruente. Este es uno de los problemas de la teoría de números que aún continúa abierto.
El problema de si un número N es congruente está relacionado con las soluciones de la ecuación y2 = x3 – N2 x (que es un ejemplo de lo que se conoce como “curva elíptica”, aunque de eso no hablaremos hoy). De hecho, estudiando esta ecuación, el matemático estadounidense Jerrold B. Tunnell (1950) obtuvo una resolución parcial del problema del número congruente.
Teorema de Tunnell: Sea N un número entero, libre de cuadrados (si es múltiplo de un número cuadrado sabemos que no es congruente, por el teorema de Fermat), y sean los conjuntos
donde el símbolo # indica la cantidad de elementos del conjunto, es decir, soluciones enteras de la correspondiente ecuación diofántica de cada conjunto. Entonces, si N es un número congruente impar, entonces f(N) = 2 g(N), y si N es un número congruente par, entonces h(N) = 2 k(N).
Además, si se verifica la conjetura de Birch y Swinnerton-Dyer (que es uno de los 7 problemas del milenio del Instituto Clay de Matemáticas, aunque en esta entrada no hablaremos de este tema) para la curva elíptica y2 = x3 – N2 x, se verificaría el recíproco, es decir, las igualdades anteriores son suficientes para afirmar que N es congruente.
En particular, si la conjetura de Birch y Swinnerton-Dyer fuese cierta, se tendría que todos los números N congruentes con 5, 6 o 7, módulo 8 (véase la entrada Un código detector de errores: la letra del DNI), serían números congruentes. En particular, los primeros números N congruentes con 5, 6 o 7, módulo 8, son: 5, 6, 7, 13, 14, 15, 21, 22, 23, 29, 30, 31, 37, 38, 39, 45, 46, 47, 53, 54, 55, … que, como podemos observar en la lista anterior, son números congruentes.
Una cuestión curiosa es la distribución de los números congruentes dentro de los números naturales. Si consideramos los 2.500 números naturales, representados en espiral, como en la espiral de Ulam (véase la entrada El poema de los números primos), y pintamos de rojo los cuadrados que se corresponden con números congruentes y de un color claro los que no lo son, la imagen que nos queda es la siguiente:

Para terminar, el número correspondiente al día de hoy, 23.022.022, se escribe en el sistema de numeración binario como:
1010111110100100111000110.
Bibliografía
1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.
2.- Página web: Numbers Aplenty.
3.- Keith Conrad, The Congruent Number Problem
4.- Wikipedia: congruent number
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
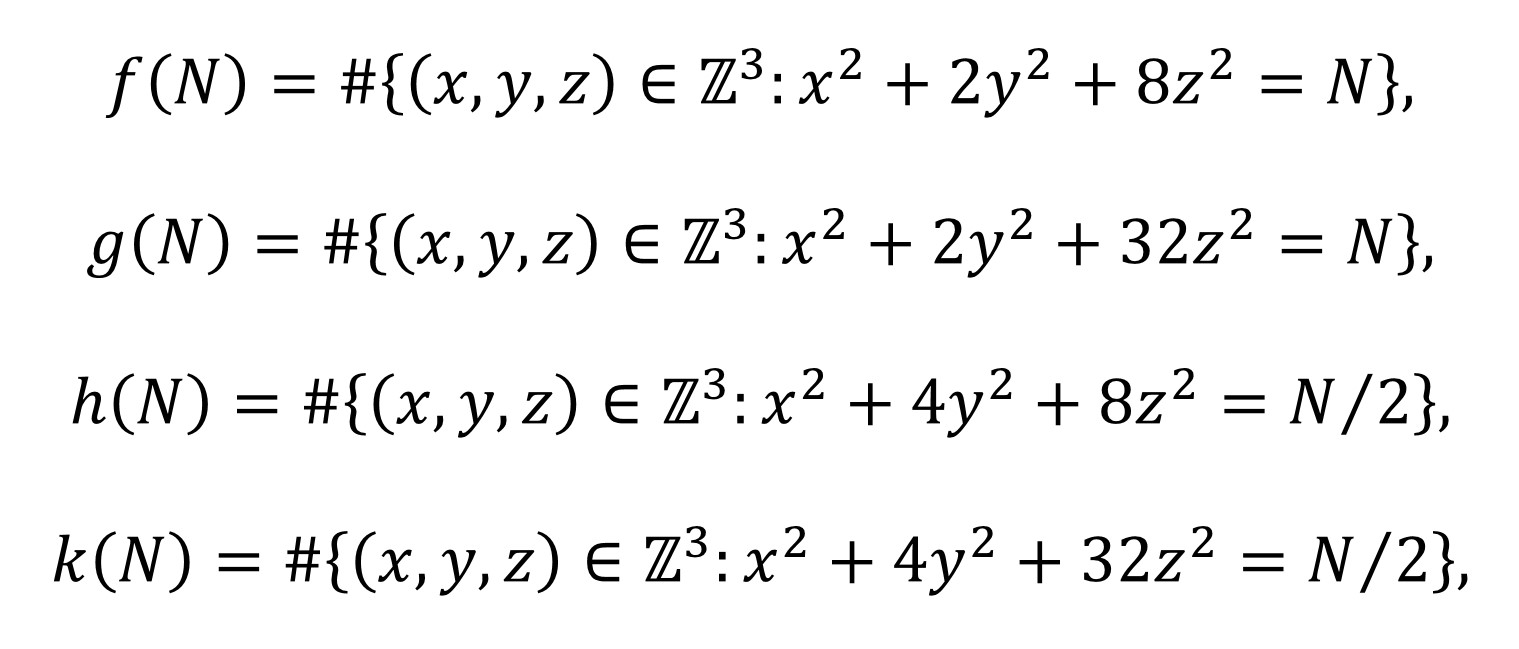
Jesús Carrero Plaza
Hay un error (a+b)/2)^2=(c)/2)^2-N, debe ser +N y viceversa en la otra ecuacion