Un objeto que manejamos prácticamente a diario en nuestra vida es el DNI, el documento nacional de identidad, que está formado por un número de ocho dígitos y, desde hace unos años, también una letra. Muchas personas piensan que esa letra se nos asigna de forma aleatoria, como el número, pero esto no es así. En esta entrada del Cuaderno de Cultura Científica vamos a explicar, aunque es posible que muchas de vosotras ya lo conozcáis, cómo se asigna esa letra y cuál es su significado.

Si nos vamos a la página web del Ministerio de Interior del Gobierno de España, que es quien emite el documento nacional de identidad, podemos leer que este es un documento público, personal e intransferible que acredita la identidad y los datos personales de su titular, y que es obligatorio para los mayores de 14 años.
Hasta hace unos años el DNI constaba solamente de un número de 8 dígitos, pero en 1990 para evitar, en la medida de lo posible, errores, se añadió una letra. Cuando rellenamos algún formulario en el que se nos pide el documento nacional de identidad es relativamente fácil equivocarnos en un dígito o cambiar dos dígitos de orden, por lo que se añadió al número del DNI un código de detección de errores, la letra.
La letra del DNI se calcula de la siguiente forma. Se toma el número del mismo, se divide por 23 y el resto de esa división nos va a dar la letra, para lo cual se utiliza una tabla que asigna a cada número, entre 0 y 22, una de las “23” letras del abecedario –, aunque son 27, se han quitado las letras I, O, U y Ñ-, de la siguiente forma:

Pongamos un ejemplo sencillo. Supongamos que el número del DNI que nos han asignado es 12.345.678. Si lo dividimos entre 23, el resto nos da 14. Miramos en el cuadro que nos asigna a cada número, entre 0 y 22, una letra y vemos que la letra asignada al número 14 es Z. Por lo tanto, el DNI será 12.345.678Z.
O si nuestro número fuese 98.765.432, entonces como al dividirlo entre 23 el resto es 5, la letra asignada es M y el DNI completo sería 98.765.432M.

Una primera cuestión que nos podemos plantear es cómo calcular el resto. Podríamos hacer la división a mano, como nos enseñaron en la escuela y calcular así el resto, como en la siguiente imagen.
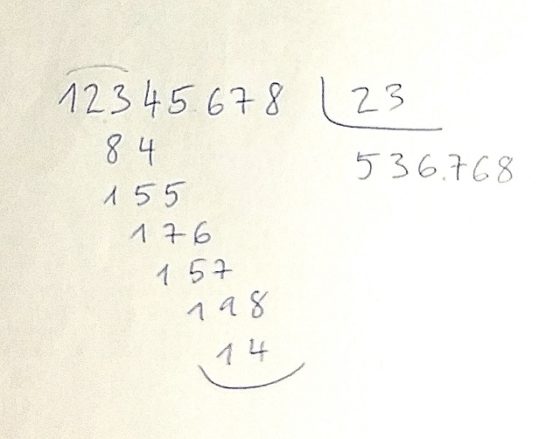
Aunque no hace falta que hagamos la división a mano para obtener el resto. Basta con utilizar una simple calculadora. Por ejemplo, si tenemos el número 12.345.678 y lo dividimos por 23 en nuestra calculadora nos dará
536.768,60869565217391304347826087…
es decir, la división nos da el número natural 536.768, seguido de una serie de decimales. Para calcular el resto a partir de este resultado, le restamos la parte no decimal, 536.768, y a lo que nos queda, la parte decimal,
0,60869565217391304347826087…
la multiplicamos por 23. El resultado, o el número más cercano al resultado, es el resto, en este caso 14.
Calcular la letra de nuestro DNI es fácil, e incluso diseñar un pequeño programa para calcularla. Más aún, hay sitios web para calcularla online si queremos ahorrarnos la división y el cálculo del resto, como la página letra NIF. Pero vayamos con algunos comentarios sobre el cálculo de la misma.
Para empezar, en la asignación de una letra asociada al número del DNI se han eliminado cuatro letras de nuestro alfabeto –que consta de 27 letras–, las mencionadas, I, O, U y Ñ. El motivo es el siguiente. Las letras I y O se han quitado para evitar confusiones con los números 1 y 0. La letra Ñ se eliminó para evitar los problemas con los sistemas informáticos del resto del mundo, donde no tienen esta letra. Las personas que la tenemos en nuestro apellido, IBAÑEZ, sabemos los problemas que da cuando viajamos en avión o vamos a algún otro país. Y la letra U se eliminó para tener un conjunto de 23 letras, ya que el número 23 es un número primo, el más grande menor que 27, lo cual es un elemento necesario para el proceso de detección de errores.
La asignación de la letra para el documento nacional de identidad, que acabamos de explicar, asegura que se van a detectar errores gracias a lo que en matemáticas se llama aritmética modular, también conocida como “aritmética del reloj”, por la analogía con las horas.

La aritmética modular, o del reloj, es un sistema aritmético que consiste en lo siguiente. Para empezar, consideramos los números enteros Z, esto es, los números naturales {1, 2, 3, …}, junto con los negativos {– 1, – 2, – 3, …} y el cero {0}, sobre los que tenemos las operaciones aritméticas básicas de la suma y la multiplicación.
![]()
Los números enteros, junto con la suma y la multiplicación, satisfacen una serie de propiedades naturales, que en matemática denominamos “estructura de anillo”, que básicamente quiere decir que cumple, más o menos, las propiedades aritméticas usuales:
i) la suma + es una operación asociativa [a + (b + c) = (a + b) + c], conmutativa [a + b = b + a], tiene un elemento neutro, el cero 0 [a + 0 = a] y tiene elemento inverso [a + (–a) = 0];
ii) la multiplicación x es una operación asociativa [a x (b x c) = (a x b) x c], tiene un elemento neutro, el 1 [a x 1 = a] y es distributiva respecto de la suma [a x (b + c) = a x b + a x c; (a + b) x c = a x c + b x c]; en este caso, además es conmutativa [a x b = b x a], por lo que hablamos de un “anillo conmutativo”.
Observemos que la multiplicación no tiene elemento inverso, ya que la división no es una operación “cerrada” en los números enteros, la división de dos números enteros puede no ser entero. Así, el inverso de 2 sería 1 / 2 = 0,5 (puesto que 2 x 0,5 = 1), sin embargo, no es un número entero.
En la aritmética modular no se considera el conjunto de todos los números enteros, sino los “números enteros módulo n”, Zn, para un cierto número natural n, que es el módulo. La idea es la siguiente. Dado el módulo n se considera el conjunto finito de n elementos Zn = {0, 1, …, n – 1}, pero, a partir del módulo, los números vuelven al principio “dando la vuelta” y cada número se asociará –de hecho, se considerarán iguales- con uno del conjunto básico {0, 1, …, n – 1}, su congruente. Así, n pasa a ser igual a 0, n + 1 igual a 1, etcétera (como las 13 horas es igual a la 1, las 14 a las 2, las 15 a las 3, …). Además, dos números enteros a y b se dice que son congruentes, módulo n, si, dentro de esa asociación que acabamos de definir, son iguales a un mismo número del conjunto básico {0, 1, …, n – 1}, lo cual ocurre (pensémoslo un poco) si a – b es divisible por n.
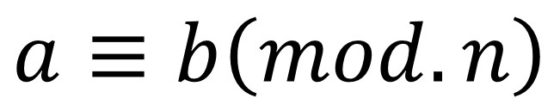
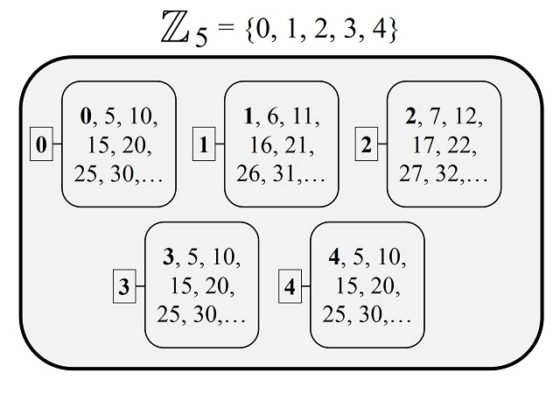
Por ejemplo, si tomamos n = 5, entonces el conjunto básico es Z5 = {0, 1, 2, 3, 4} y tenemos que, por ejemplo, 5 es congruente con 0 (módulo 5), 6 es congruente con 1 (módulo 5), 7 es congruente con 2 (módulo 5) o, por ejemplo, que 13 es congruente con 3 (módulo 5).
Esto es algo así como dividir los números enteros en 5 conjuntos y que los elementos de cada conjunto se consideren iguales.
Una vez considerado el conjunto de los números enteros módulo n, se restringen las operaciones aritméticas de la suma y la multiplicación al mismo. Por ejemplo, para el conjunto de los números enteros módulo 5, Z5 = {0, 1, 2, 3, 4}, se tiene que 2 + 3 = 0 (observemos que en este conjunto los números 2 y 3 son inversos el uno del otro, respecto de la suma), 3 + 3 = 1 o 3 + 4 = 2, para la suma, y 2 x 3 = 1 (esto es, que el 2 y el 3 son inversos respecto de la multiplicación), 2 x 4 = 3, o 4 x 4 = 1 (el cuatro es inverso de sí mismo), para la multiplicación.
Podemos dibujar las tablas de estas dos operaciones sobre el conjunto Z5 de los números enteros módulo 5.
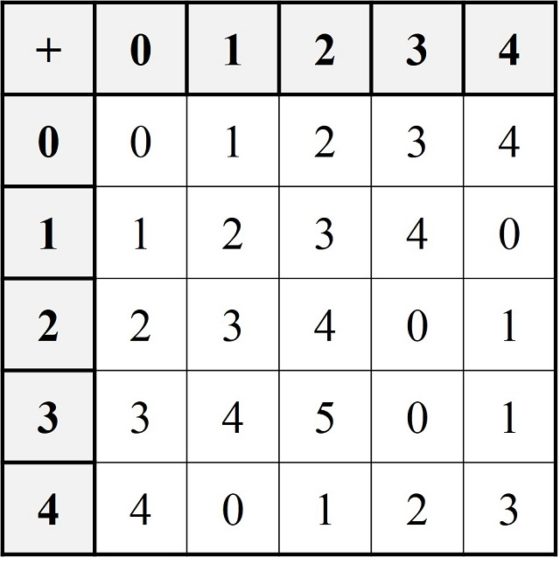
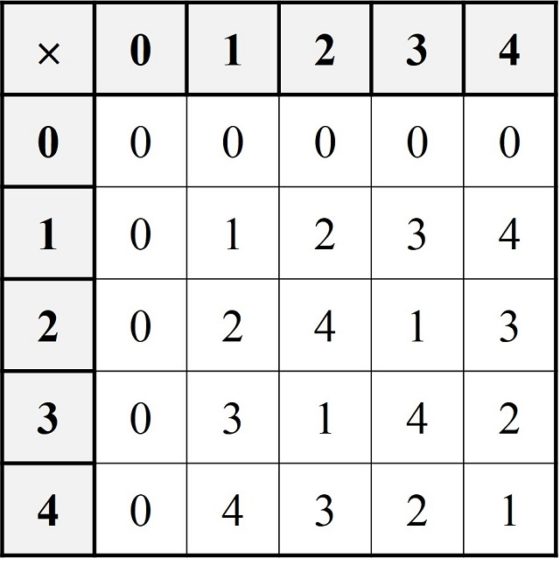
Podemos observar que Z5 ha heredado las propiedades aritméticas de la suma y la multiplicación que se cumplían sobre los números enteros Z. Por lo tanto, Z5 también tiene estructura de anillo conmutativo. En general, Zn, los números enteros módulo n, para cualquier n, tienen estructura de anillo conmutativo con las operaciones de suma y multiplicación heredadas de los números enteros, Z.
Dibujemos ahora las tablas aritméticas sobre el conjunto Z6.
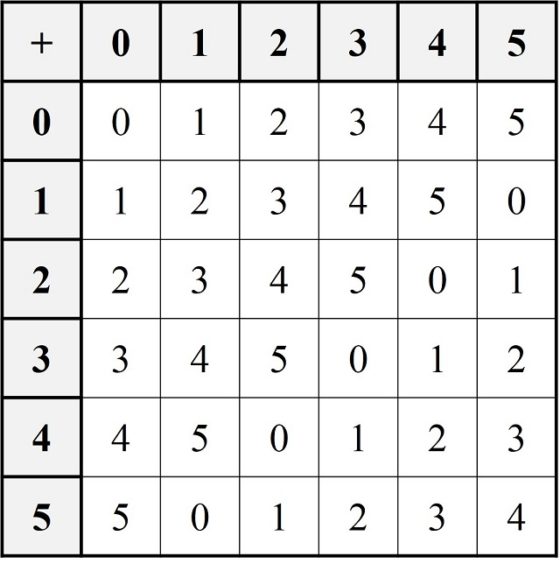
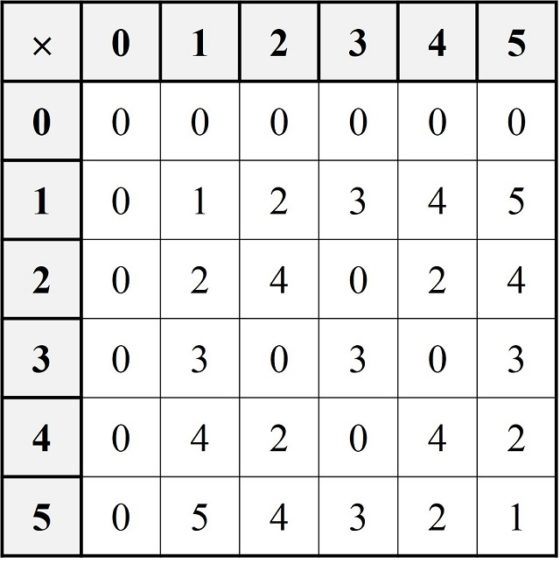
Lo primero que podemos observar es que en Z6 existen “divisores del cero”, es decir, números a y b tales que su multiplicación es igual a 0, a x b = 0, lo cual no ocurría para los números enteros Z (y, dicho sea de paso, tampoco para Z5). En concreto tenemos que en Z6 se satisface que 2 x 3 = 0 o que 3 x 4 = 0.
Por otra parte, como ocurría en los números enteros, Z, no todos los elementos no nulos de Z6 tienen inverso respecto a la multiplicación. No lo tienen ni 2, ni 3, ni 4, aunque sí 5, que es inverso de sí mismo. Pero si nos fijamos en Z5, aquí si tienen inverso, respecto de la multiplicación, todos los elementos no nulos. De hecho, esta propiedad es más general aún, ya que los enteros módulo un número primo p, Zp, satisfacen que todos los elementos no nulos tienen inverso, respecto de la multiplicación. En matemáticas, si tenemos un anillo conmutativo que satisface que existen también inversos respecto de la multiplicación se dice que tiene “estructura de cuerpo”. Por lo tanto, los enteros módulo un número primo p, Zp, tienen estructura de “cuerpo”.
Y aquí es donde volvemos a enlazar con el documento nacional de identidad, puesto que para asignar la letra hemos considerado los enteros módulo el número primo 23, Z23, que tiene estructura matemática de “cuerpo”.
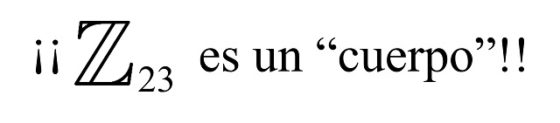
Ahora, utilizando la aritmética modular se pueden demostrar algunos resultados que nos permiten demostrar que la letra del DNI es un código detector de errores. Por ejemplo, puede demostrarse el siguiente resultado.
Teorema 1: La letra del DNI permite detectar un error.
Es decir, si nos hemos equivocado al escribir uno de los dígitos del DNI –el resto de dígitos y la letra están bien–, entonces detecta el error, o lo que es lo mismo, en ese caso la letra asociada al número incorrecto no podrá ser esa misma letra. Por ejemplo, dos números del DNI que solo se diferencian en un dígito, como 12.345.678 y 12.395.678, no pueden tener la misma letra. Efectivamente, esos números tienen dos letras distintas 12.345.678Z y 12.395.678N.
La demostración del teorema 1 es relativamente sencilla. Recordemos que para que dos números enteros p y q determinen el mismo número módulo 23 se tiene que cumplir que p – q sea divisible por 23. Si tenemos dos números de DNI A y B que solo se diferencian en un dígito (es decir, hemos cometido un error), entonces A – B = 10n x (a – b), donde n es la posición del dígito que es distinto (de derecha a izquierda) y a y b son los dígitos que son diferentes. Por ejemplo, en el caso anterior 12.395.678 – 12.345.678 = 90.000 – 40.000 = 105 x (9 – 4). Pero como 10n no es divisible por 23 (solo lo es por 2, 5 y potencias de ambos), para que A – B sea divisible por 23 (y a ambos números les corresponda el mismo número en Z23, luego la misma letra en la asignación descrita), tendría que ocurrir que a – b fuese divisible por 23. Pero, resulta que a y b son números entre 0 y 9, luego la única forma de que a – b sea divisible por 23 es que a – b = 0, es decir, a = b, con lo cual no habría error. En nuestro ejemplo, con 12.395.678 – 12.345.678, el número 5 tendría que ser divisible por 23, que no lo es, por eso los dos números tienen asignadas letras distintas. Y con este razonamiento queda demostrado el resultado del teorema 1.

Sin embargo, la letra no permite detectar dos errores en el DNI, es decir, existen números de DNI que difieren en dos dígitos y tienen la misma letra. Por ejemplo, 12.345.678 y 12.345.655 ambos tienen la letra Z: 12.345.678Z y 12.345.655Z. Observemos que 12.345.678 – 12.345.655 = 23.
El código de detección de errores que es la letra del DNI permite detectar más errores aún.
Teorema 2: La letra del DNI permite detectar el intercambio de dos dígitos consecutivos en el número del DNI.
Por ejemplo, dos números que difieran únicamente en el orden de dos dígitos consecutivos, como 12.345.678 y 12.346.578 no pueden tener la misma letra. Así, 12.346.578 tiene asociada la letra V (12.346.578V) y no la letra Z como 12.345.678Z. La demostración de este resultado es similar al anterior, pero la dejamos para aquellas personas que quieran intentar realizar la demostración por ellas mismas (quien esté interesado puede ver las demostraciones de estos resultados en el artículo Algunos secretos del documento nacional de identidad español: una aplicación de la aritmética modular a códigos detectores de errores).
A continuación, démosle la vuelta a la asignación de la letra a nuestro número del documento nacional de identidad. Imaginemos ahora que queremos obtener un número de DNI con una letra concreta, por ejemplo, la B. ¿Cómo lo haríamos? Lo primero que debemos saber es cuál es el número de resto asociado a esa letra. En este caso, para la B, es 11. A continuación, tomamos un número cualquiera, por ejemplo, 69.134.572, cuya letra es la E, 69.134.572-E, ya que el resto es 22. Como la B se corresponde con el 11 y nos ha salido el resto 22, entonces restamos 22 – 11 = 11 a nuestro número, 69.134.572 – 11 = 69.134.561. Efectivamente, sería 69.134.561B.

Para terminar esta entrada del Cuaderno de Cultura Científica, algunas creencias relativas al documento nacional de identidad.
Creencia 1: “Los primeros dígitos identifican la provincia”. Esto es falso. Los números del DNI se asignan, en la actualidad, de forma aleatoria según se expiden. Aunque en el pasado los números del documento nacional de identidad se asignaban por lotes a las comisarías de policía que se dedicaban a la realización de los documentos nacionales de identidad, por eso, nos podíamos encontrar con conocidos que tuviesen los mismos primeros números de nuestro DNI.
Creencia 2: “Los números del DNI de las personas fallecidas se vuelven a poner en circulación”. Esto también es falso. Como decíamos al principio de esta entrada, el documento nacional de identidad es un documento personal e intransferible que acredita la identidad y los datos personales de su titular. Utilizando números de 8 dígitos tenemos 99.999.999 posibles números (recordemos que la población de España en 2.020 era de 47,35 millones) y todavía no se han agotado.
Creencia 3: “Los números del DNI que empiezan con 0 pertenecen a personas fallecidas”. Tampoco esto es verdad. Los números de DNI que empiezan por 0 muchos de ellos fueron así expedidos cuando se asignaban a mano, mientras que los que se conceden en la actualidad, son lotes de números recuperados que por algún momento cuando correspondía otorgarlos, no se utilizaron.
Creencia 4: “El número de la parte de atrás de nuestro documento nacional de identidad nos indica el número de personas que se llaman como nosotros”. Esto sería gracioso, pero no es cierto. La parte de atrás de nuestro DNI contiene tres líneas de caracteres que están diseñadas para su lectura por dispositivos de reconocimiento de texto. Consiste en información sobre nosotros y sobre el documento, así como diferentes dígitos de control, pero ninguna relación con las personas que se llaman como nosotros.
Creencia 5: “En la parte de atrás del DNI se indican tus antecedentes penales”. Tan falso como lo anterior.
Creencia 6: “Los primeros números del DNI corresponden a la familia real”. Esto sí es cierto. Cuando se creó el documento nacional de identidad, en tiempos del dictador Francisco Franco, este se quedó con el número 1, su mujer Carmen Polo con el número 2 y su hija Carmen Franco el número 3. Por su parte, la familia real tiene reservados los números que van del 10 al 99. El rey emérito Juan Carlos I tiene el 10 y la reina Sofía el 11. Las infantas Elena y Cristina tienen el 12 y el 14 (se saltaron el 13, seguramente por motivos supersticiosos). Por este motivo, cuando el Ministerio de Hacienda publicó un comunicado que decía “el error en la imputación de transmisiones de inmuebles a la Infanta Cristina es consecuencia de que la información recibida por la Agencia Tributaria figura atribuida a un DNI que coincide con el suyo”, no parecía este un argumento muy creíble, ya que la infanta tiene un DNI singular, 14Z. Seguimos, el rey Felipe VI tiene el número de DNI 15, la princesa Leonor el 16 y la infanta Sofía el 17.
Creencia 7: “El primer DNI expedido fue el del general Francisco Franco”. A pesar de que Franco tenía el número 1 en su documento nacional de identidad, sin embargo, no fue el primer DNI expedido. El primer Documento Nacional de Identidad fue expedido el 20 de marzo de 1951, aunque fue en 1944 cuando se aprobó el decreto que regulaba estos documentos de identificación personal. Ese primer documento tenía el número 19.103.001, que había sido adjudicado en los lotes al equipo de Valencia. Pertenecía a Eva García Ayala, que era la mujer de un fotógrafo valenciano, que quería mostrar a sus clientes que en su establecimiento también se podían hacer fotografías para el nuevo documento nacional de identidad.
Pero no se vayan todavía. Terminamos, ahora sí, la entrada con algunas de las propuestas de diseños para el documento nacional de identidad que se presentaron en el concurso de 1946. Pueden verse más en el artículo Así podría haber sido el DNI: los diseños descartados de los años 40 y 80.


Bibliografía
1.- Página web del Ministerio del Interior del Gobierno de España sobre el Documento Nacional de Identidad
2.- Historia del Documento Nacional de Identidad [PDF]
3.- Varios autores, Sesenta años de expedición del Documento Nacional de Identidad 1951-2011, Fundación Policía Española, 2013.
4.- Ramón Esteban-Romero, Algunos secretos del documento nacional de identidad español: una aplicación de la aritmética modular a códigos detectores de errores, Modelling in Science Education and Learning 9 (2), 59-65, 2016.
5.- La verdad: Mitos y leyendas del DNI que creías ciertos y no lo son
6.- Huffington Post: 4 leyendas urbanas sobre el DNI y 6 detalles que quizá no conocías
7.- Hoy: Una identidad acartonada
8.- La cabeza llena: Así podría haber sido el DNI: los diseños descartados de los años 40 y 80
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Un código detector de errores: la letra …
[…] Un objeto que manejamos prácticamente a diario en nuestra vida es el DNI, el documento nacional de identidad, que está formado por un número de ocho dígitos y, desde hace unos años, también una letra. Muchas personas piensan que esa letra se nos asigna de forma aleatoria, como el número, pero esto no es […] […]
Cas típic 3515: noi li agrada la tetera de l’assassí | Pons's blog
[…] El codi de detector d’errors de la lletra del DNI […]