En mi anterior entrada en el Cuaderno de Cultura Científica, “Quipu y yupana, instrumentos matemáticos incas (I)”, estuvimos hablando del sistema de numeración inca, que es un sistema de numeración decimal y posicional, como también lo es el sistema de numeración indo-arábigo que utilizamos de forma generalizada en la actualidad, pero cuyas cifras básicas son nudos que se realizan sobre cuerdas que cuelgan de una cuerda principal en los quipus.

Los quipus servían para representar los números, relacionados con los diferentes usos de estos instrumentos matemáticos y sociales, sin embargo, no servían para realizar operaciones aritméticas como sumas, restas, multiplicaciones y divisiones. Como mucho podían registrar los resultados de una operación aritmética, como mostramos en la anterior entrada con la suma de cuatro cantidades y su resultado, 658 = 38 + 273 + 258 + 89.

Para realizar las operaciones aritméticas utilizaban una especie de ábaco, que el cronista José de Acosta (1540-1600) menciona en su texto Historia Natural y Moral de las Indias, como “quipus de granos de maíz”.

“… pues verles otra suerte de quipos, que usan de granos de maíz, es cosa que encanta; porque una cuenta muy embarazosa, en que tendrá un muy buen contador que hacer por pluma y tinta, para ver a como les cabe entre tantos, tanto de contribución, sacando tanto de acullá y añadiendo tanto de acá, con otras cien retartalillas, tomarán estos indios sus granos y pondrán uno aquí, tres acullá, ocho no sé dónde; pasarán un grano de aquí, trocarán tres de acullá, y, en efecto, ellos salen con su cuenta hecha puntualísimamente sin errar un tilde, y mucho mejor se saben ellos poner en cuenta y razón de lo que cabe a cada uno de pagar o dar, que sabremos nosotros dárselo por pluma y tinta averiguado. Si esto no es ingenio y si estos hombres son bestias, júzguelo quien quisiere, que lo que yo juzgo de cierto es que, en aquello que se aplican, nos hacen grandes ventajas.”

El jesuita José de Acosta nos describe la destreza con la cual los indios realizaban sus operaciones aritméticas con este instrumento de contabilidad inca, el “quipu de granos de maíz”, que hoy se conoce con el nombre de “yupana” (que procede del término quechua “yupay” que significa contar) o, simplemente, “ábaco inca”.

Sin embargo, en el texto de José de Acosta no se describe cómo es ese dispositivo para realizar operaciones aritméticas, ni cómo funciona. Otro tanto pasa en el texto Comentarios reales de los Incas (1609) del escritor e historiador Gómez Suárez de Figueroa (1539-1616), apodado el Inca Garcilaso de la Vega, que también se maravilla con el manejo que tenían del ábaco al decir que “hacían las cuentas con piedrezuelas y las sacaban tan ajustadas y verdaderas…”. En dicho texto también menciona que los indios sabían mucho de geometría y de aritmética.

Pero respecto al instrumento para realizar esos cálculos, el ábaco inca o yupana, solo es mínimamente descrito en dos fuentes de la época. La primera es la Historia del Reino de Quito y crónica de la provincia de la compañía (1789), del sacerdote jesuita Juan de Velasco (1727-1792), quien se refiere a “ciertos archivos o depósitos hechos de madera, de piedra o de barro, con diversas separaciones, en las cuales se colocaban piedrecillas de distintos tamaños, colores y figuras angulares”. Se correspondería con una serie de artefactos encontrados en excavaciones arqueológicas, como el que aparece en la imagen anterior, y que se conocen como “yupanas arqueológicas”.

La otra fuente sobre la yupana es la imagen del quipucamayo que aparece en el texto Nueva corónica i buen gobierno (1615), del cronista Felipe Guamán Poma de Ayala, dibujado junto a los dos instrumentos matemáticos incas, el quipu y la yupana.

Esta imagen es la única “especie de explicación” que existe sobre el ábaco inca y su funcionamiento. A partir de la misma se ha intentado reconstruir su funcionamiento, pero debido a la falta de información que supone esa única imagen, existen muchas teorías que intentan explicarlo. Veremos algunas de ellas.

En la mayoría de intentos de explicar el funcionamiento de la yupana de Poma de Ayala se considera que, de forma similar a los quipus, el sistema de numeración que está detrás de la yupana es un sistema de numeración posicional decimal. Cada una de las filas se correspondería con una de las potencias de diez, las posiciones de la representación del número, es decir, las unidades (1), decenas (10), centenas (100), unidades de millar (1.000) y decenas de millar (10.000).

La interpretación más antigua se debe al antropólogo sueco Henry Wassen (1908-1996), que aparece en su artículo The ancient peruvian abacus (1931). En su interpretación de la ilustración de Poma de Ayala los círculos blancos representarían huecos del ábaco en los que colocar los maíces o piedrecitas, de forma que los círculos negros de la imagen representarían huecos en los que ya se han colocado los maíces. Además, Wassen asigna a cada una de las columnas, de izquierda a derecha, los valores 1, 5, 15, 30. Es decir, cada maíz en la primera columna de la izquierda tendría el valor de 1, dentro de la posición correspondiente en función de la fila, cada maíz de la segunda columna tendría el valor 5, el valor 15 en la tercera y 30 en la última.

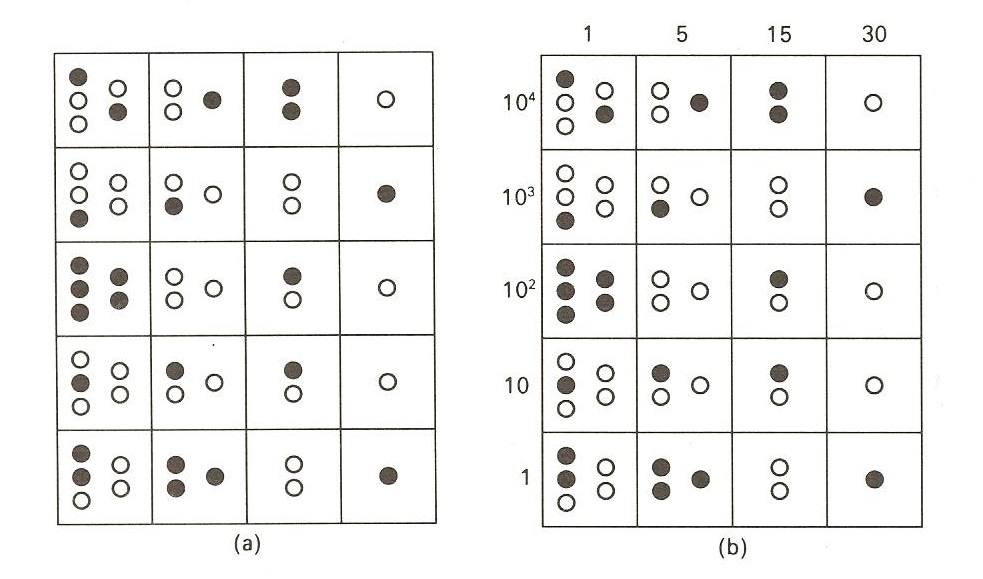
De esta forma, la yupana representada por Poma de Ayala estaría representando al número 408.257. En la primera fila, la de las unidades, tendríamos 2 maíces en la primera columna (2 × 1), más tres en la segunda (3 × 5), ninguno en la tercera (0 × 15) y un maíz en la cuarta columna (1 × 30), en total, 2 + 15 + 30 = 47. De la misma forma se realizaría el cálculo para las demás filas, obteniéndose el resultado mencionado,

47 + 21 × 10 + 20 × 100 + 36 × 1.000 + 37 × 10.000 = 408.257.

Una de las cuestiones que llaman la atención de esta interpretación es que hay números que se pueden representar de varias formas. Por ejemplo, el número 47 mencionado antes también se podría obtener como (2, 0, 1, 1), es decir, 2 maíces en la primera columna, ninguna en la segunda, 1 en la tercera y 1 en la cuarta, frente a la representación anterior (2, 3, 0, 1). Aunque esto bien podría tener la intención de dejar espacios para manejar los maíces en el propio proceso de la operación aritmética.

Aunque una de las mayores críticas a esta interpretación de la yupana, motivo por el cual se quedaría rápidamente desfasada, es la complejidad de la misma.

George G. Joseph en su libro La cresta del pavo real realizó una interpretación similar, pero más sencilla, y en su opinión más plausible que la de Wassen, de la yupana de Poma de Ayala. Para Joseph los maíces o piedrecillas de cada columna tendrían siempre el valor de una unidad (1), pero en la primera columna solo se podrían colocar 5 maíces, es decir, habría 5 huecos, en la segunda 3 maíces, en la tercera 2 y en la última 1.

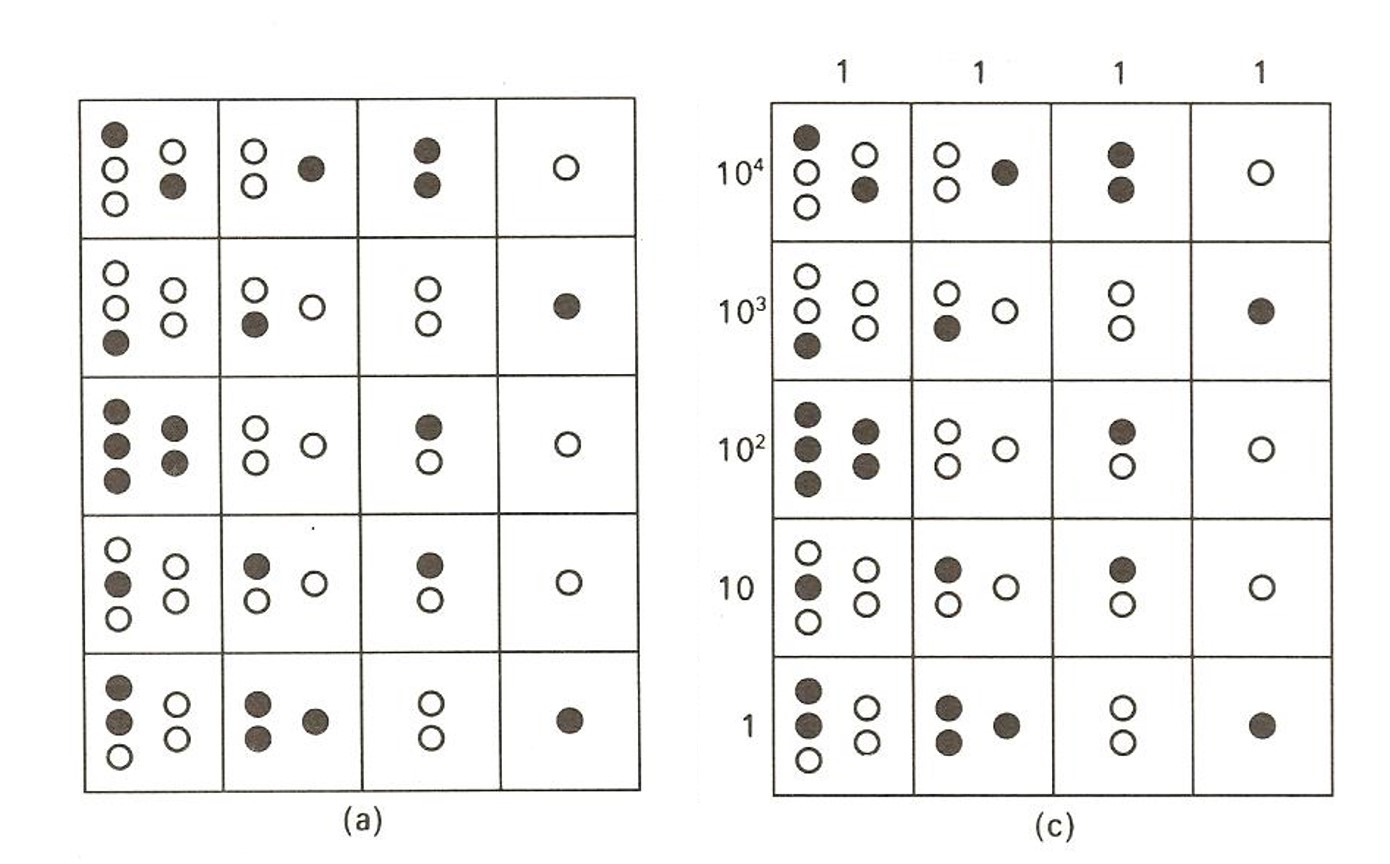
De esta forma, el valor representado en la ilustración del ábaco inca de Poma de Ayala sería 53.636, puesto que sería

6 + 3 × 10 + 6 × 100 + 3 × 1.000 + 5 × 10.000 = 53.636.

Una observación rápida de esta interpretación de la ilustración de Nueva corónica i buen gobierno, me hace preguntarme que de ser esta la interpretación correcta, cuál es el motivo por el cual los maíces (círculos negros en la imagen) están colocados en esas posiciones y no en otras. Por ejemplo, tanto en la primera fila como en la tercera hay 6 maíces en cada una de ellas que representan el 6 en cada una de las posiciones, pero están colocadas en diferentes posiciones, mientras que, si el objetivo es solamente representar a los números, sería más lógico y en orden, de izquierda a derecha, rellenando huecos.

Una posible explicación estaría en el hecho de que la yupana no es simplemente para representar números, sino para realizar operaciones aritméticas, y Poma de Ayala podría estar representando el resultado de una operación aritmética, por ejemplo, una multiplicación, de forma que los maíces habrían quedado en la posición consecuencia de los movimientos de la operación aritmética.

George G. Joseph se aventura a intentar explicar cómo serían las operaciones aritméticas con la yupana, según su interpretación de la misma. Como él mismo comenta, la adición y la sustracción no plantearían muchos problemas, y la forma de realizarse sería más o menos sencilla.

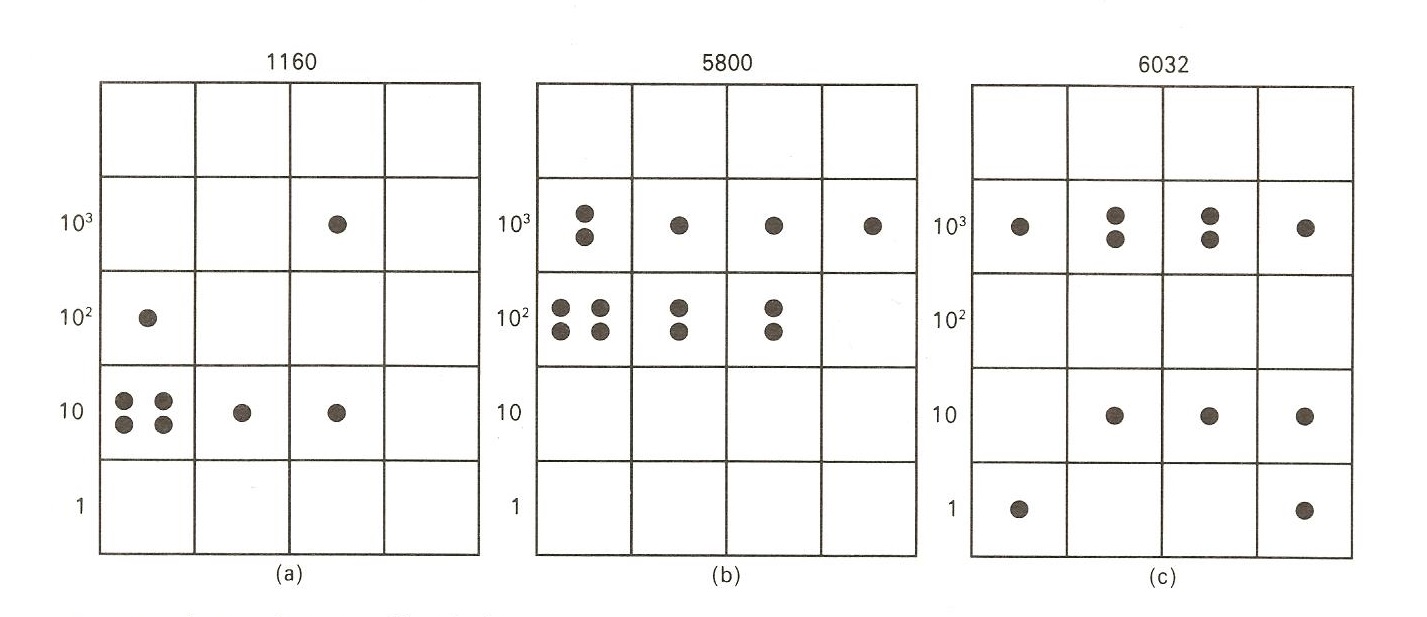
Pero realiza la siguiente conjetura sobre el mecanismo de multiplicación con el ábaco inca. Supongamos que se quieren multiplicar los números 116 y 52. Teniendo en cuenta que 52 es igual a 5 × 10, primero se desplazaría una fila hacia arriba la representación del número 116 con maíces, es decir, se obtendría el número 1.160 (10 × 116). Ahora se sumaría 1.160 a sí misma 5 veces (5 × 1.160), obteniendo 5.800. Y finalmente se añadiría dos veces 116 al resultado anterior, obteniéndose el valor buscado, 6.032, como se muestra en la imagen de abajo.

El método es esencialmente utilizar la idea de multiplicación sobre una numeración posicional, ya que

116 × 52 = 116 × (5 × 10 + 2) = 116 × 10 × 5 + 116 × 2,

de forma análoga a como se realiza en otros procedimientos de multiplicación para sistemas posicionales.

El historiador italiano radicado en Perú, Carlo Radicati di Primeglio (1914-1990), propone también una interpretación en la que cada maíz simboliza una unidad, como en el caso de Joseph, pero en su opinión se podían poner hasta nueve maíces en cada recuadro, y no 5, 3, 2 y 1, como sugiere la imagen del texto de Poma de Ayala. A partir de esa suposición construye toda una serie de procedimientos para sumar, restar, multiplicar y dividir, que pueden verse en su texto El sistema contable de los Incas, Yupana y Quipu (1976).

Para terminar la entrada de hoy del Cuaderno de Cultura Científica veamos la última de las interpretaciones, que podríamos clasificar como clásicas, tanto por el momento en que son formuladas, como por el hecho de que mantienen la suposición de un sistema de numeración de la yupana es decimal y posicional. Es la propuesta del ingeniero textil británico William Burns Glynn (1923-2014), quien cuando llegó a Perú quedó fascinado por el arte textil peruano y por los quipus, y es quien propuso el nombre de “yupana” para el ábaco inca.

La propuesta, en cuanto a la representación de los números dentro del ábaco, es similar a la propuesta por George G. Joseph, con la diferencia de que solo son válidas para la representación de los números las tres primeras columnas (con 5, 3 y 2 huecos para piedras), mientras que la última columna sería la columna de la “memoria”, y que sería un elemento fundamental para los métodos de cálculo.

Por lo tanto, en cada fila puede haber hasta 10 piedras (5 + 3 + 2), y cuando se tienen las 10 piedras, se pueden sustituir por una de memoria mientras se está computando, lo cual equivale a una piedra en la siguiente fila (hacia arriba). Por ejemplo, en la siguiente imagen se representa el número 53.906, según el modelo de Glynn.

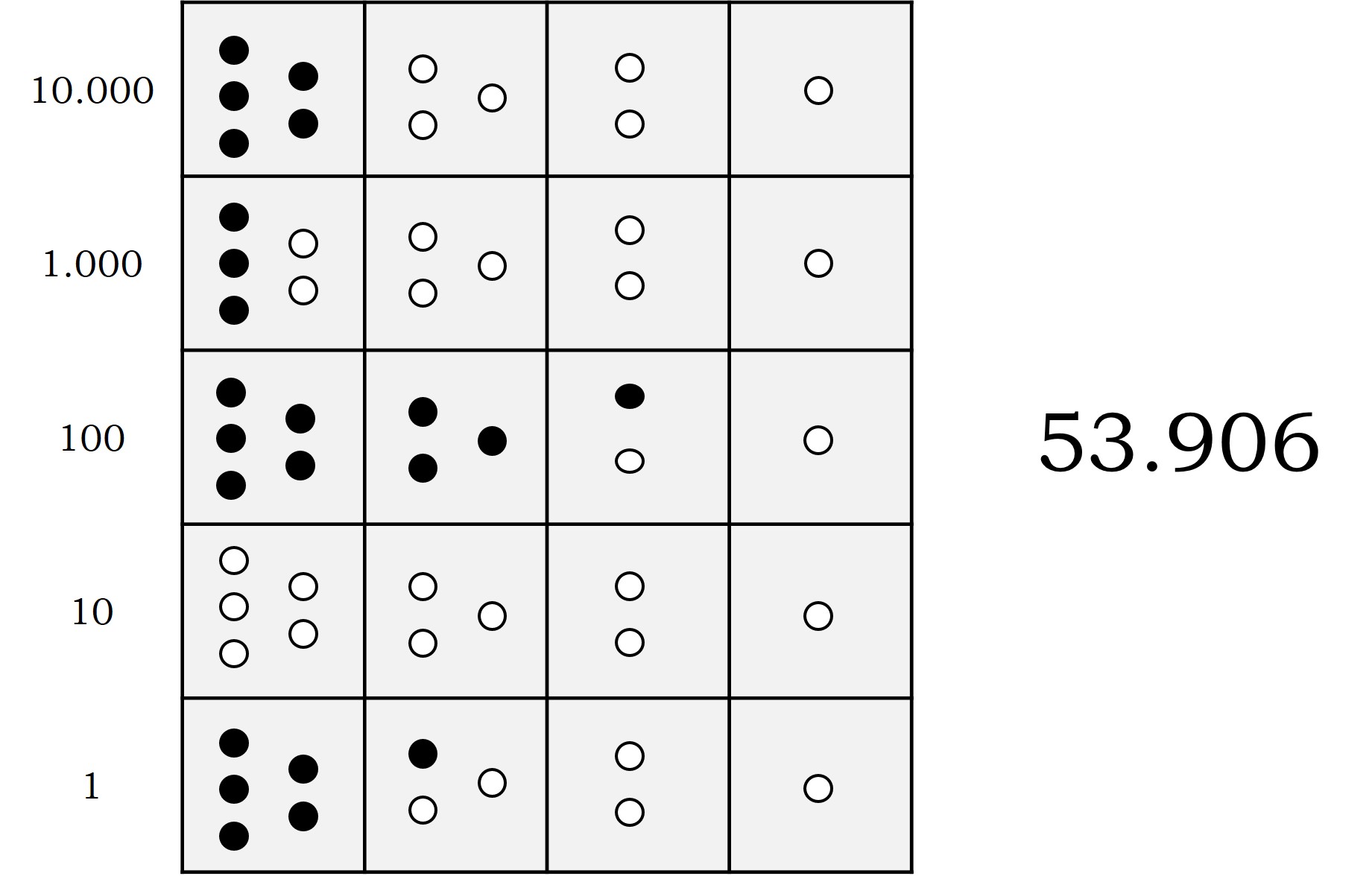
A partir de la interpretación de William Burns Glynn de la yupana, este propone los posibles métodos para realizar las operaciones aritméticas que podrían utilizar en el imperio inca. Veamos el sencillo proceso de suma, que esencialmente es el mismo que en cualquier otro ábaco.

Supongamos que queremos sumar 489 y 754. En primer lugar, se colocan las piedras en la yupana representando uno de los números, por ejemplo, el 489, y se colocan las fichas que representarían el otro número fuera de la yupana, al lado de la memoria, como se muestra en la imagen.

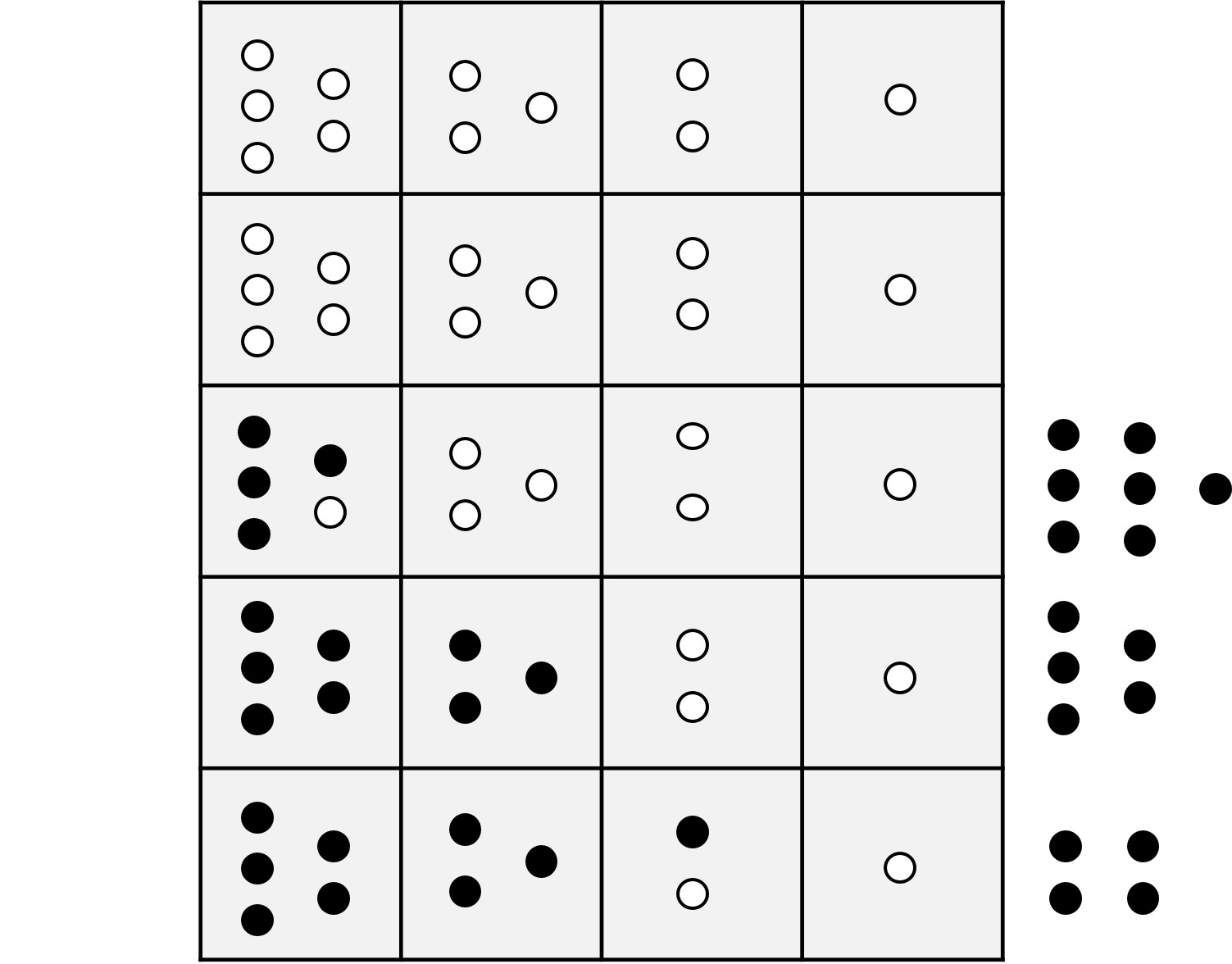
A continuación, se empiezan a meter piedras de las unidades que están en el lateral dentro de la yupana hasta completar las 10 (5 + 3 + 2), en este caso solo una y quedando tres aún en el lateral. Una vez completadas las diez se recogen y se pone una en la parte de la memoria, quedando como en la siguiente imagen.

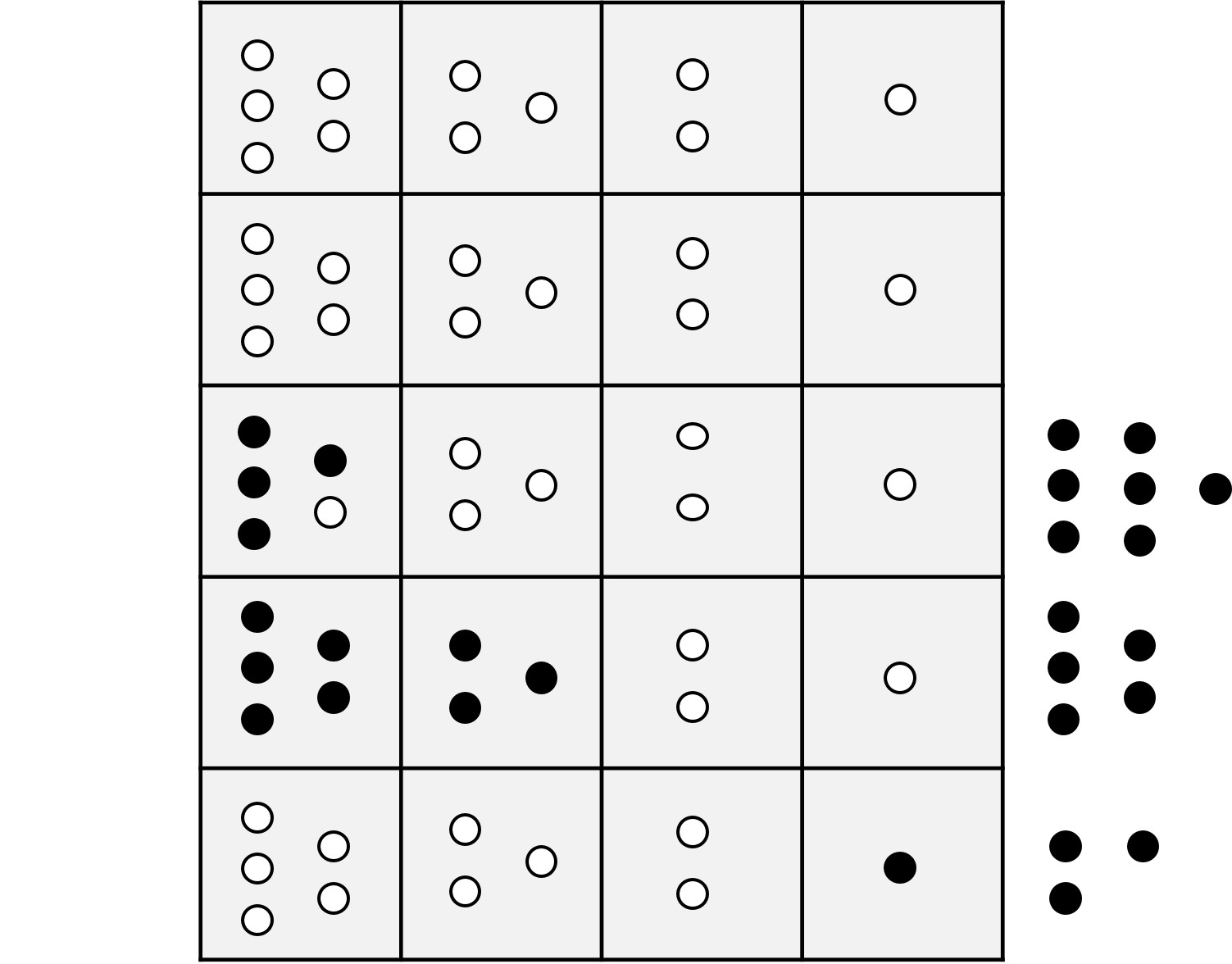
Como ya quedan huecos libres en las unidades de la yupana, se colocan las piedras que aún quedan en el lateral, que son tres, y después, la piedra de la memoria se pasa a la siguiente fila, en este caso, a la de las decenas. El resultado es el siguiente.

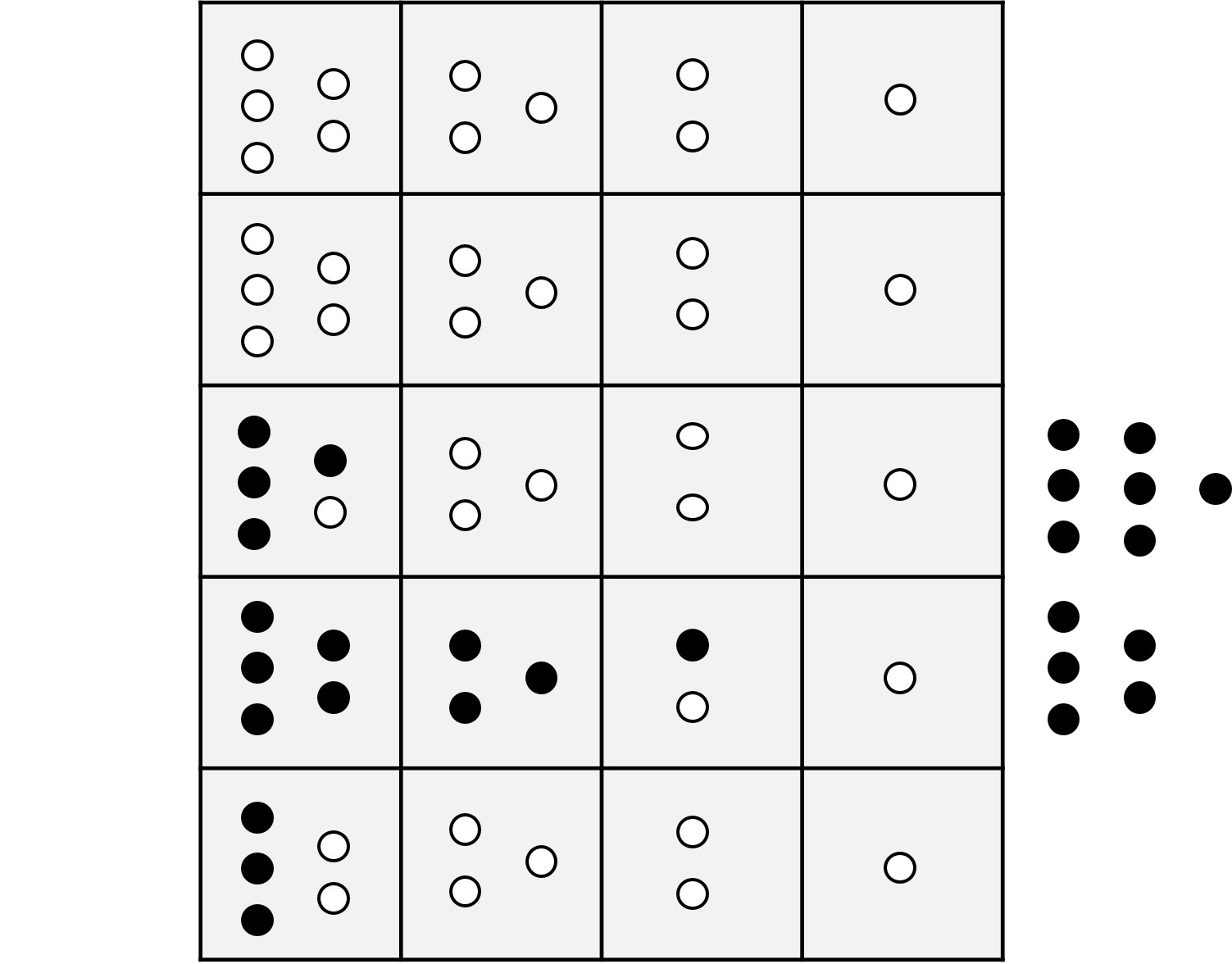
Una vez que hemos terminado con las piedras laterales de las unidades, se realiza la misma operación para las decenas. Solo queda un hueco libre en la segunda fila, la de las decenas, luego se coloca una de las piedras laterales de las decenas y como se ha completado la fila, se quitan las 10 piedras de esa segunda fila y se pone, en su lugar, una piedra de memoria. Además, han quedado libres los huecos, por lo que se colocan las piedras restantes del lateral de las decenas, que, en este caso, son 4. El resultado es el siguiente.

Como antes, la piedra que está en la memoria (en la parte de las decenas) se traslada a la siguiente fila de la yupana, la de las centenas. Y de nuevo, se incorporan las piedras del lateral, que en este caso son 7, a la zona de la yupana, y cuando se complete la fila se quitan las 10 piedras y se coloca una en la memoria, dejando sitio para continuar colocando las piedras del lateral. Y no nos olvidemos de subir la piedra de la memoria, a la siguiente fila, en este caso, la de las unidades de millar (como se muestra en la siguiente imagen). Como ya no hay más piedras en el lateral para añadir se ha concluido la suma y el número que queda representado es el resultado, 489 + 754 = 1.243.

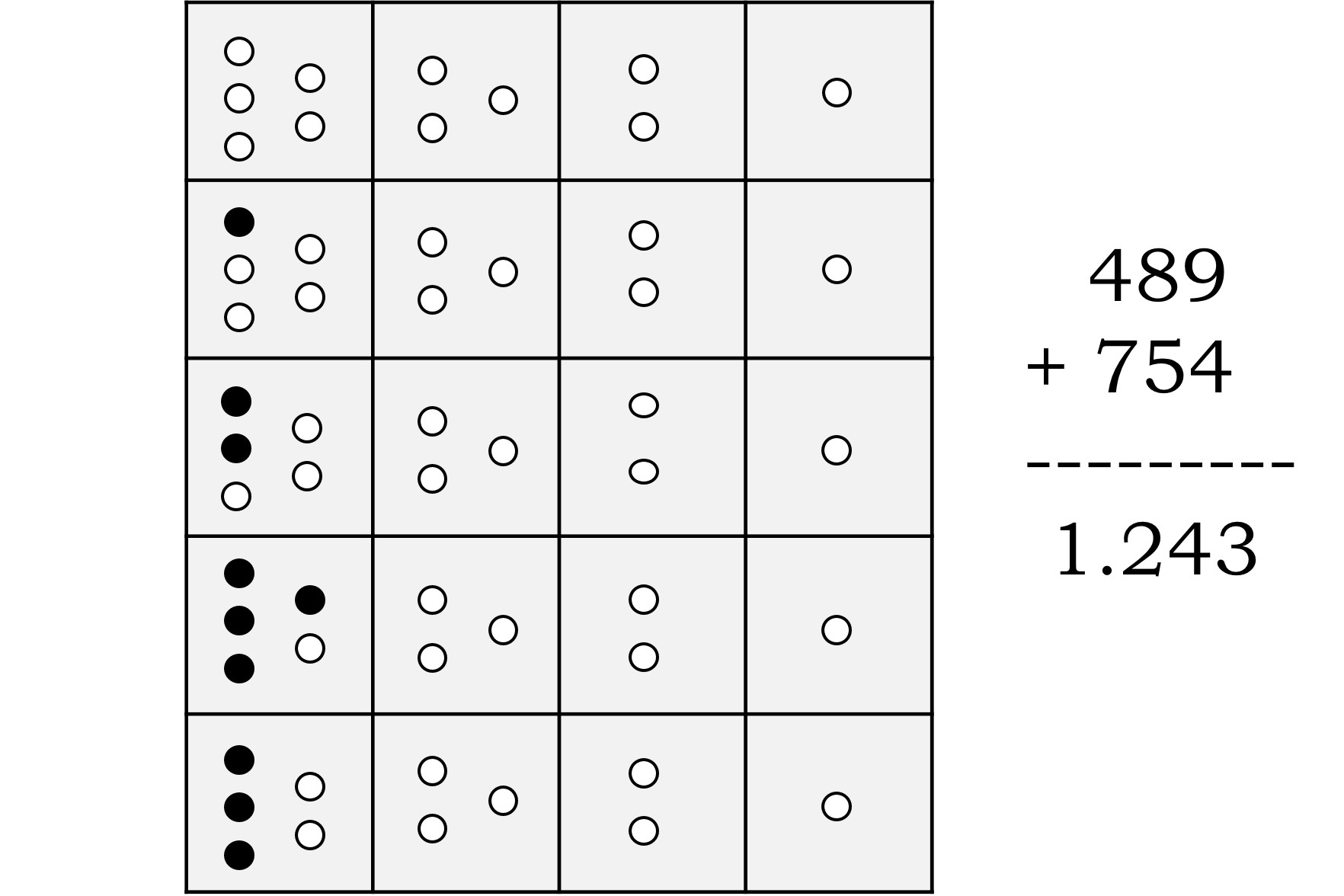
La interpretación de Glynn de la yupana de Poma de Ayala ha alcanzado cierta popularidad y se está utilizando en la enseñanza, como una nueva herramienta didáctica.

Existen más interpretaciones del ábaco inca que aparece en la ilustración de la Nueva corónica i buen gobierno de Felipe Guamán Poma de Ayala, algunas abandonan la condición de decimal del sistema de numeración y otros la condición de ser un sistema posicional. Pero de estas otras interpretaciones más modernas hablaremos en otra ocasión.

Bibliografía

1.- Raúl Ibáñez, Quipu y yupana, instrumentos matemáticos incas (I), Cuaderno de Cultura Científica, Mayo, 2018

2.- Carlos Radicati de Primeglio, El sistema contable de los Incas, Yupana y Quipu, Librería Studium, 1976.

3.- Carlos Radicati de Primeglio, Estudios sobre los quipus, UNMSM, Fondo Editorial; COFIDE; Istituto Italiano di Cultura, 2006.

4.- Diego Pareja, Instrumentos prehispánicos de cálculo: el quipu y la yupana, revista Integración, Departamento de Matemáticas UIS, vol. 4, n. 1, p. 37-55, 1986.

5.- Felipe Guamán Poma de Ayala, Nueva corónica i buen gobierno, 1615. Versión online en la Biblioteca Real Danesa

6.- José de Acosta, Historia natural y moral de las Indias, 1589. Versión online en la Biblioteca Virtual Miguel de Cervantes, 1999.

7.- George Gheverghese Joseph, La creta del pavo real, Las matemáticas y sus raíces no europeas, Pirámide, 1996.

8.- Henry Wassen, The ancient Peruvian abacus, Comparative Ethnological Studies 9, p. 191-205, 1931.

9.- William Burns Glynn, La Tabla de Cálculo de los Incas, Lima, 1981.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica