En la mítica novela Contacto (1985), del astrónomo y divulgador científico estadounidense Carl Sagan (1934-1996), que sería posteriormente llevada al cine en 1997 por el director Robert Zemeckis, famoso por películas como Regreso al futuro (1985) o Forrest Gump (1994), los extraterrestres envían un mensaje, en forma de impulsos de radio, que consiste en una lista de números primos.

“… lo que estamos recibiendo semeja una larga secuencia de números primos, números enteros solo divisibles por sí mismos y por uno. Como ningún proceso astrofísico genera números primos, me atrevería a suponer que, de acuerdo con todos los criterios que conocemos, esto tiene visos de ser auténtico. […]

– El hecho de que yo sea asesor presidencial sobre temas científicos no significa nada –dijo él–, puesto que mi campo es la biología. Por eso le pido que me explique todo muy despacio. Entiendo que, si la fuente emisora se halla a veintiséis años luz, el mensaje debió de haber sido enviado hace veintiséis años. Digamos que, en la década de los sesenta, unos hombrecitos de aspecto extraño y orejas puntiagudas quisieron hacernos saber cuán aficionados eran a los números primos. Sin embargo, los números primos no son difíciles, o sea que ellos no estarían haciendo alarde de nada. Esto más bien se parece a un curso de recuperación de matemáticas. Quizá deberíamos sentirnos ofendidos.

–No –repuso ella con una sonrisa–. Piénselo de este modo. Todo esto no es más que una señal para atraer nuestra atención. Habitualmente recibimos impulsos insólitos provenientes de cuásares, púlsares y galaxias. Sin embargo, los números primos son muy específicos, muy artificiales. Por ejemplo, ningún número par es también primo. Nos cuesta creer que alguna galaxia en explosión o plasma radiante pueda emitir un conjunto de señales matemáticas como estas. Los números primos tienen como objeto despertar nuestra curiosidad.

–Pero ¿para qué? –preguntó él, desconcertado.

–No lo sé, pero en estas cuestiones es preciso armarse de paciencia. A lo mejor, dentro de un tiempo dejan de enviarnos números primos y los reemplazan por otra cosa, algo más significativo, el mensje verdadero. No nos queda más remedio que seguir escuchando.

Esa era la parte más difícil de explicar al periodismo: que las señales no tenían ningún sentido. Eran solo los primeros centenares de números primos, en orden, para comenzar otra vez desde el principio. 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31…

El 9 no era número primo, sostenía Ellie, porque era divisible por 3 (además de por 9 y 1, desde luego). El 10 tampoco lo era, porque era divisible por 5 y por 2 (además de por 10 y 1). El 11 sí era número primo, ya que solo era divisible por 1 y por sí mismo. Sin embargo, ¿por qué optaban por transmitir dichos números? Pensó en un idiot savant, una de esas personas deficientes en destrezas comunes, verbales o sociales, pero también capaces de realizar complicadísimas operaciones matemáticas tales como calcular al momento en qué día de la semana va a caer el 1 de junio del año 6977. No lo hacen para nada, sino solo porque les gusta, porque son capaces de hacerlo…”

Los números primos son muy importantes desde el punto de vista matemático, y juegan un papel fundamental en todas las áreas de las matemáticas, en particular, en la aritmética y la teoría de números. Esto seguramente se deba a que los números primos son los ladrillos con los que se contruye todo el edificio de los números naturales, como nos dice el teorema fundamental de la aritmética, es decir, todo número natural se puede expresar como producto de números primos, de forma única. Además, los números primos tienen importantes aplicaciones para nuestra sociedad, siendo la más conocida el sistema de codificación RSA, dentro de la criptografía, que se basa precisamente en la factorización de los números naturales como producto de números primos.

Pero no es ni la importancia de los números primos, fuera y dentro de las matemáticas, ni las aplicaciones de los mismos, el objetivo de esta entrada del Cuaderno de Cultura Científica, sino el problema de la distribución de los números primos dentro de los números naturales, o más bien, la distribución de los no primos.

Aunque empecemos por el principio. Los números primos son aquellos números naturales que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 25 no es primo ya que se puede dividir por 5 (además de por 1 y 25), o tampoco el 27 (divisible por 3 y 9), mientras que el número 19 sí es primo, ya que solamente es divisible por el 1 y él mismo, al igual que lo son los números 2, 3, 5, 7, 11 y 13, entre otros. A los números que no son primos, se les llama números compuestos. El número 1 no se considera primo, ya que en ese caso la factorización de los números naturales (teorema fundamental de la aritmética) no sería única, siempre se puede multiplicar por 1, pero tampoco se considera compuesto.

Si empezamos por los primeros números primos… el primero es el 2. Y es obvio que todos los múltiplos de 2 no van a ser números primos, puesto que son divisibles por 2, es decir, podemos quitar a todos los números pares de la lista de candidatos a números primos. Siguiendo el orden natural dentro de los números, nos encontramos con el siguiente número primo, el 3, y podemos quitar todos los múltiplos de 3 de la lista de candidatos a números primos. El siguiente número que no hemos eliminado y, por lo tanto, es primo, es el 5, luego podemos tachar a todos los múltiplos de 5 de la lista de números primos, y así continuamos con los múltiplos de 7, 11, 13, 17, 19, etc… Este es el conocido como método de la criba Eratóstenes (matemático griego del siglo III a.c.) para obtener los números primos, mediante la eliminación de los múltiplos de los primos que se van obteniendo.

En la siguiente imagen, hemos incluido la criba de Eratóstenes, pero solo con números impares (ya hemos eliminado los múltiplos de 2, los pares), para números más pequeños que 361 = 19². Hemos dibujado las líneas de los múltiplos de 3, 5, 7, 11, 13 y 17, con las cuales ya hemos eliminado todos los números compuestos menores que 361. Los números que quedan son todos los números primos menores que 361.

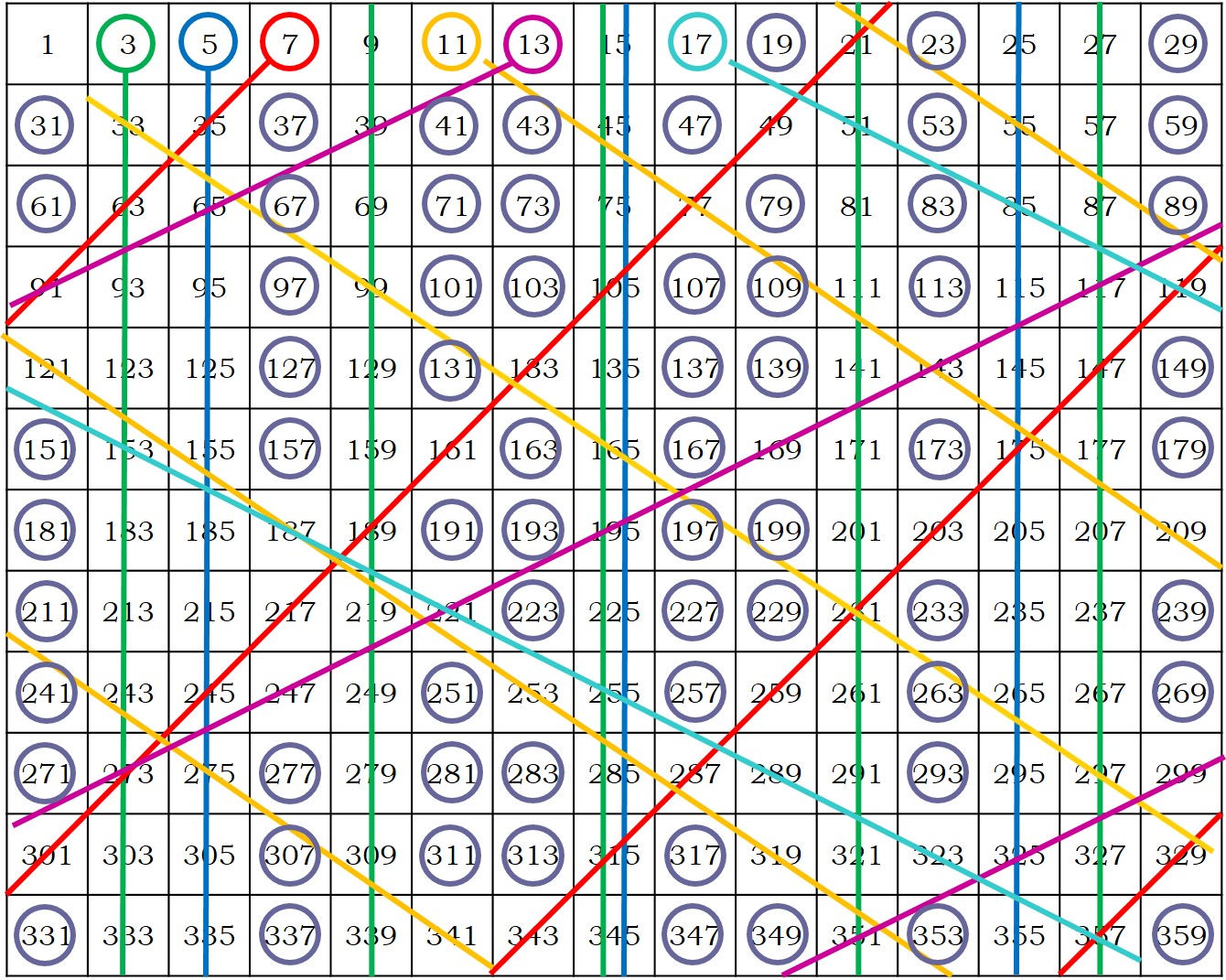
La Criba de Eratóstenes nos permite ir obteniendo los números primos desde el 2 en adelante, pero es un método lento para obtener números primos, aunque con paciencia y muchos, muchos cálculos pueden obtenerse tablas de primos. La primera tabla amplia de números primos fue obtenida en 1606 por el matemático italiano Pietro Cataldi (1548 – 1626), que mostraba los números primos menores que 800. Así, se fueron obteniendo tablas cada vez más largas. Los primos menores que 1.020.000 fueron obtenidos en 1811 por el matemático húngaro Ladislaus Chernac (1742-1816) y hasta 100.330.200 se llegó hacia 1863, por el matemático nacido en la ciudad del imperio austriaco Lenberg (ahora ciudad ucraniana de Lviv) Jakob Philipp Kulik (1793-1863). Kulik estuvo 20 años preparando su tabla, que ocupó 8 volúmenes manuscritos con un total de 4.212 páginas. Al morir Kulik, que había dedicado su vida a la obtención de tablas matemáticas, se dijo de él: “ha dejado de calcular y de vivir”. Este tipo de tablas de números primos incluía también las descomposiciones en factores primos de los números compuestos. Todo esto antes de la era de los ordenadores.

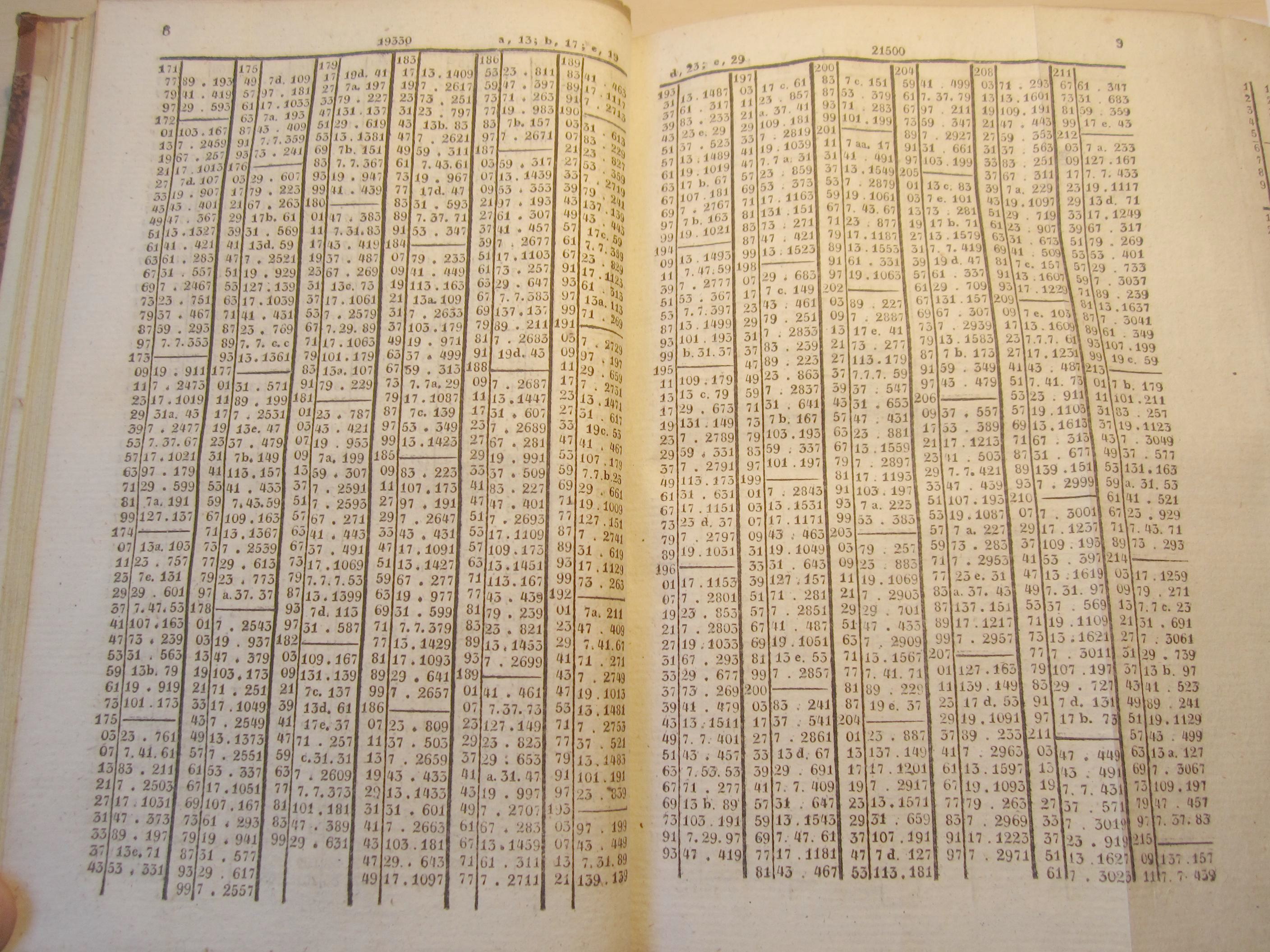
Sin embargo, el método descrito por Eratóstenes no nos permite saber si un cierto número alto, por ejemplo, 28.295.303, es primo o no, salvo que se tenga ya la tabla que alcance a ese número. Para saberlo tendríamos que ver si se puede dividir por todos los números primos menores que él, lo cual es complicado como ya menciona el gran matemático alemán Carl Friedrich Gauss (1777-1855) en su obra Disquisitiones Arithmeticae (1801). Por cierto, el número 28.295.303 es compuesto y se puede dividir por 269, 293 y 359.

“El problema de distinguir los números primos de los compuestos y de descomponer estos últimos en sus factores primos se sabe que es uno de los más importantes y útiles de la aritmética. Ha ocupado el trabajo y la sabiduría de los geómetras antiguos y modernos hasta tal extremo que sería superfluo tratar el problema en toda su extensión… Es más, la propia dignidad de la ciencia parece requerir que se explore todo medio posible para la solución de un problema tan elegante y tan famoso.”
[Disquisitiones Arithmeticae, 1801, Carl F. Gauss]

Con el método de la Criba de Eratóstenes podemos ir obteniendo primos “lentamente” y con muchos cálculos. Son los números que quedan al ir eliminando los múltiplos de los primos que vamos obteniendo. Así, se puede ir consiguiendo cada vez más números primos, por lo que la primera cuestión evidente que nos podemos plantear es si llegará algún momento en que nos quedemos sin números primos, es decir, ¿hay una cantidad finita o infinita de números primos?

Los griegos ya conocían la respuesta a esta pregunta. A pesar de lo que afirma uno de los personajes de la novela La conjetura de Perelman (Ediciones B, 2011), del escritor murciano Juan Soto Ivars, la matemática Ludmila, madre en la novela de Grigory Perelman, “Se han hecho listas de números primos con ese método de comprobación, pero no se sabe si más allá siguen existiendo. No sabemos si son infinitos porque no sabemos cómo se generan”, existe una cantidad infinita de números primos.

La demostración aparece recogida en la gran obra Los Elementos del matemático griego Euclides (aprox. 325-265 a.c.). En concreto, la Proposición 20, del Libro IX, de Los Elementos, dice así “Los números primos son más que cualquier cantidad propuesta de números primos”.

El argumento de Euclides es el siguiente. Si existiese una cantidad finita de números primos, p₁, p₂, …, p_n, se puede construir un número más grande que los números p₁, p₂, …, p_n-1 y p_n, pero que no es divisible por ninguno de ellos, a saber, el número p₁x p₂x … x p_n + 1, en consecuencia, o es primo o es divisible por un primo que no es ninguno de los anteriores. Por lo tanto, existen infinitos números primos.

Por ejemplo, si consideramos los cinco primeros primos números primos 2, 3, 5, 7 y 11, podemos construir el número

2 x 3 x 5 x 7 x 11 + 1 = 2.311,

que no se puede dividir por ninguno de los números primos 2, 3, 5, 7 o 11. De hecho, 2.311 es otro número primo. O si tomamos los seis primeros números primos

2 x 3 x 5 x 7 x 11 x 13 + 1 = 30.031,

se obtiene un número que no se puede dividir por ninguno de esos seis números primos, pero como no es primo, se tiene que poder factorizar mediante números primos mayores que 13, como así es, 30.031 = 59 x 509, ambos dos nuevos primos.

Volvamos a la idea de la Criba de Eratóstenes. Cuantos más números primos se van obteniendo, mayor cantidad de números compuestos se pueden generar como multiplicación de los mismos y sus potencias, que son los que vamos descartando en este método de obtención de los números primos. Por lo tanto, aunque sabemos que existen infinitos números primos, da la impresión de que cada vez hay menos, ya que generamos muchísimos números compuestos, ¿será esto cierto o se irá manteniendo más o menos constante la cantidad de primos que van apareciendo dentro de los números naturales?

Miremos los listados de números primos. Si miramos la Criba de Eratóstenes anterior, observaremos que entre los 100 primeros números hay 25 primos, es decir, 1 de cada 4 números es primo. Sin embargo, si miramos entre los 1.000 primeros números, resulta que hay 168 que son primos, 1 de cada 6 números. Un porcentaje menor. Y así, como podemos ver en la siguiente tabla, según vamos ampliando la cantidad de números considerados, existe un menor porcentaje de números primos. Luego según vamos avanzando en la recta de números naturales, los números primos van siendo cada vez más infrecuentes, y los números compuestos van ocupando más el espacio dentro de los números naturales.

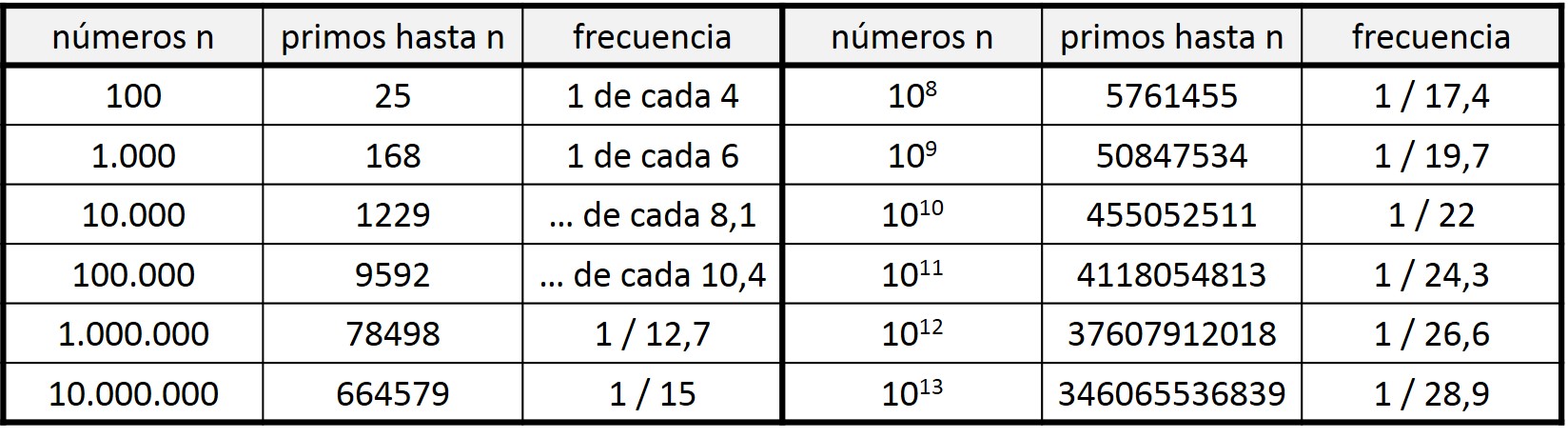
El problema de la distribución de los números primos dentro de la recta de los números naturales es un problema importante de la teoría de números, relacionado con uno de los siete problemas del milenio “la hipótesis de Riemann”, del que ya hablaremos en el Cuaderno de Cultura Científica en otra ocasión. En esta entrada queremos hacer una pequeña reflexión sobre el problema dual, la distribución de los números compuestos.

Si volvemos a mirar la imagen de la Criba de Eratóstenes anterior observamos que al principio hay muchos números primos y la distancia entre ellos no es muy grande. Los primos 2 y 3 están pegados. Entre los primos 3 y 5, 5 y 7, 11 y 13, o 17 y 19, solamente hay un número par (de hecho, los números primos que están tan cerca, que solo les separa un número par, se llaman números primos gemelos). Entre los primos 7 y 11, 13 y 17, o 19 y 23, hay un hueco de tres números compuestos. Poco más adelante encontramos un hueco de cinco números no primos, entre el 23 y el 29, y un hueco de siete lo encontramos entre los números 89 y 97. El hueco más grande de números compuestos entre los menores de 361, que son los que aparecen en esa tabla, lo encontramos entre los números 113 y 127, que es una laguna sin números primos de 13 números compuestos. Al igual que entre los números 317 y 331.

Como hemos comentado anteriormente, cada vez hay menos números primos y más números compuestos, por lo que nos podemos plantear si existen lagunas de números compuestos tan grandes como queramos, que tengan, al menos, 100, 1.000, 1.000.000 o cualquier otra cantidad de números compuestos.

Si miramos en la literatura matemática descubriremos que el primer hueco con más de 100 números compuestos se produce a partir del número primo 370.261. De hecho, hay 111 números compuestos entre ese primo y el siguiente. Esta laguna fue encontrada por el matemático inglés James Whitbread Lee Glaisher (1848-1928) en 1877.

La primera laguna de más de 1.000 números compuestos nos la encontramos a partir del número primo 1.693.182.318.746.371. Entre este número primo y el siguiente existen 1.131 números compuestos consecutivos. Esta laguna fue obtenida por el matemático sueco Bertil Nyman en 1999.

Pero, ¿existen lagunas de números compuestos, entre dos números primos, tan grandes como queramos? La respuesta es afirmativa.

A continuación, vamos a mostrar una sencilla técnica para obtener este tipo de lagunas, para la cual necesitamos utilizar el factorial de un número. Recordemos que el factorial de un número n, que se denota n!, se define como el producto de todos los números naturales desde 1 hasta n,

n! = 1 x 2 x 3 x … x (n – 1) x n.

Aquí podéis ver un pequeño video, de la sección Una de mates del programa Órbita Laika (año 2015) de La 2, con una explicación sobre el significado del factorial de un número.

Ahora, vamos a construir lagunas de números compuestos, entre números primos, de tamaños tan grandes como deseemos. Pero vayamos poco a poco. Imaginemos que queremos encontrar dos números primos entre los cuales haya, por lo menos, 4 números compuestos consecutivos. Entonces consideramos los números

5! + 2 = 122, 5! + 3 = 123, 5! + 4 = 124, 5! + 5 = 125,

que resulta que no son números primos, ya que, por ejemplo, 5! + 2, es divisible por 2, puesto que 5! + 2 = 1 x 2 x 3 x 4 x 5 + 2 = 2 x (1 x 3 x 4 x 5 + 1), sacando el 2 como factor común. De igual forma, 5! + 3 es divisible entre 3, 5! + 4 entre 4 y 5! + 5 entre 5, luego no son primos. En consecuencia, entre el primo anterior a 122 y el siguiente a 125 se genera una laguna con, al menos, 4 números primos. Aunque, de hecho, es la laguna que hemos comentado anteriormente, entre 113 y 127, que tiene 13 números compuestos consecutivos entre ambos.

Si se desea construir una laguna de, al menos, 7 números no primos consecutivos, utilizando esta técnica, se considera el factorial de 8, que da lugar a los siguientes 7 números compuestos no consecutivos:

8! + 2, 8! + 3, 8! + 4, 8! + 5, 8! + 6, 8! + 7 y 8! + 8.

Si tenemos en cuenta que 8! = 40.320, entonces los números compuestos anteriores son 40.322, 40.323, 40.324, 40.325, 40.326, 40.327 y 40.328.

En general, si buscamos una laguna con al menos n números compuestos consecutivos, debemos de considerar el factorial de (n + 1), con el que podemos generar los n números compuestos siguientes

(n + 1)! + 2, (n + 1)! + 3, …, (n + 1)! + (n + 1).

Esta técnica es válida para cualquier número n. Luego el punto fuerte de este resultado es que nos asegura la existencia de lagunas de números compuestos tan grandes como queramos, aunque como ponen de manifiesto los ejemplos anteriores, esas lagunas pueden no ser óptimas en los siguientes sentidos.

La laguna de números no primos consecutivos puede ser más grande que el n del que partimos, como en el primer ejemplo, para el cual n = 4, luego aseguramos una laguna de, al menos, 4 elementos, pero realmente la laguna llega a tener 13 elementos. La otra cuestión es que para generar una laguna de, al menos, 8 números compuestos nos vamos al número 40.322 y los siguientes, aunque realmente una laguna con al menos 8 números no primos la encontramos ya entre los primeros números naturales, ya que como hemos comentado antes, entre los números primos 113 y 127, hay 13 números que no son primos. La cosa es más grave aún para números mayores, por ejemplo, 1000 (que tampoco es que sea excesivamente grande), ya que 1001! es un número enorme, con 2.571 dígitos, en contraste con la laguna de, al menos, 1000 números compuestos consecutivos vista anteriormente.

Bibliografía

1.- Clifford A. Pickover, La maravilla de los números, Ma Non Troppo, 2002.

2.- John Conway, Richard K. Guy, The book of numbers, Springer-Verlag, 1996.

3.- Enrique Gracián, Los números primos, un largo camino al infinito, El mundo es matemático, RBA, 2010.

4.- Wikipedia: Prime Number Theorem

5.- Eric W. Weisstein, Prime Gaps, fromMathWorld-A Wolfram Web Resource.

6.- Thomas R. Nicely, First occurrence prime gaps

7.- Página web del humorist gráfico Sydney Harris

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica