En esta entrada del Cuaderno de Cultura Científica vamos a hablar de un concepto sencillo, pero que da mucho juego, los números pandigitales.

Se dice que un número es pandigital si está formado por todas las cifras básicas (incluyendo o no, el número 0), de forma que cada cifra aparece una única vez, como en los números 321.576.984 (sin incluir el 0) o 9.753.102.468 (incluyendo el 0). A estos números en los que cada cifra básica aparece una única vez se les denomina números pandigitales restringidos, en contraposición con los números pandigitales redundantes en los que hay repeticiones de cifras básicas, es decir, cada dígito aparece al menos una vez, como en los números 1.223.445.667.889 o 10.203.040.506.070.809.
Existen 9! = 362.880 números pandigitales restringidos sin cero, desde el número 123.456.789, que es el más pequeño, al número 987.654.321, que es el mayor. Esto se debe a que todos los números pandigitales restringidos sin 0 se obtienen mediante todas las permutaciones de las nueve cifras básicas {1, 2, 3, 4, 5, 6, 7, 8, 9}, de manera que cada permutación da lugar al número pandigital que consiste en las cifras del 1 al 9 colocadas en el orden que determina la permutación (por ejemplo, la permutación {2, 4, 6, 8, 1, 3, 5, 7, 9} tiene asociado el número 246.813.579 o la permutación {2, 1, 4, 3, 6, 5, 8, 7, 9} el número 214.365.879), luego como existen 9! permutaciones de nueve elementos (véase la entrada Buscando lagunas de números no primos), esta es la cantidad de números pandigitales restringidos sin cero que existen.
Por otra parte, cada uno de los números pandigitales restringidos de los anteriores, sin cero, como 123.456.789 da lugar a nueve números pandigitales restringidos con cero, en función de en cuál de las 9 posiciones posibles coloquemos la cifra 0. Así, el número 123.456.789 da lugar a los nueve números que van desde 1.023.456.789 hasta 1.234.567.890. Por lo tanto, en total hay 9 x 9! = 3.265.920 números pandigitales restringidos con cero. Respecto a los números pandigitales redundantes, con o sin cero, claramente existen infinitos.
Ejemplos curiosos de números pandigitales
A. El número pandigital restringuido más pequeño es 123.456.789 (sin cero) y 1.023.456.789 (con cero), mientras que el más grande es 987.654.321 (sin cero) y 9.876.543.210 (con cero).
El número pandigital 123.456.789 es un número curioso ya que si lo multiplicamos por 8 nos da otro número pandigital, que casi (con la excepción del “12” y “21”) es el recíproco del anterior, 123.456.789 x 8 = 987.654.312. Más aún, multiplicando por 2, 4, 5 y 7 seguimos teniendo números pandigitales.
123.456.789 x 2 = 246.913.578,
123.456.789 x 4 = 493.827.156,
123.456.789 x 5 = 617.283.945,
123.456.789 x 7 = 864.197.523,
123.456.789 x 8 = 987.654.312.
Si tomamos números pandigitales restringidos, que incluyan el cero, también nos encontramos ejemplos tales que algunos de sus múltiplos también son pandigitales. Por ejemplo, el número pandigital 1.098.765.432 al multiplicarlo por 2, 4, 5 y 7 da como resultados números pandigitales.
1.098.765.432 x 2 = 2.197.530.864,
1.098.765.432 x 4 = 4.395.061.728,
1.098.765.432 x 5 = 5.493.827.160,
1.098.765.432 x 7 = 7.691.358.024.
O el número pandigital (sin cero) 987.654.321 se transforma en números pandigitales (con cero) al multiplicarlo por 2, 4, 5, 7 y 8.
987.654.321 x 2 = 1.975.308.642,
987.654.321 x 4 = 3.950.617.284,
987.654.321 x 5 = 4.938.271.605,
987.654.321 x 7 = 6.913.580.247,
987.654.321 x 8 = 7.901.234.568.
Más aún, la diferencia entre este, el número pandigital restringido (sin cero) más grande, y 123.456.789, el número pandigital restringido (sin cero) más pequeño, sigue siendo un número pandigital (sin cero).
987.654.321 – 123.456.789 = 864.197.532.
B. No existen números pandigitales restringuidos primos.
Recordemos que los números primos son aquellos números que solamente se pueden dividir por 1 y por ellos mismos, como los números 2, 3, 5, 7, 11, 13 o 19, mientras que números como 6, que también se puede dividir por 2 y 3, o 25, también divisible por 5, no son primos. Sabemos que no existen números pandigitales restringidos primos por el criterio de divisibilidad del número 9, es decir, un número es divisible por 9 si, y sólo si, la suma de sus dígitos es divisible por 9 (véase la entrada Las curiosas reglas de divisibilidad), puesto que la suma de los dígitos de un número pandigital restringido, tenga o no cero, es igual a 45, que es divisible por 9.
Pero sí existen números pandigitales redundantes primos. Los primeros (con cero) son 10.123.457.689, 10.123.465.789, 10.123.465.897, 10.123.485.679, etc., que forman la sucesión denominada A050288 en la Enciclopedia On-line de Sucesiones de Números Enteros (OEIS).

Si consideramos los números pandigitales redundantes sin cero, entonces el primer primo es 1.123.465.789, seguido de los siguientes 1.123.465.879, 1.123.468.597, 1.123.469.587, 1.123.478.659, etc. que forman la sucesión A050290 de la Enciclopedia On-line de Sucesiones de Números Enteros.
C. El único número pandigital restringido sin cero (respectivamente con cero) que es “polidivisible” es 381.654.729 (resp. 3.816.547.290).
Recordemos, ya que no es un concepto habitual, que un número es polidivisible, también llamado mágico, si verifica las siguientes propiedades: su primer dígito (por la izquierda) es no nulo, sus dos primeros dígitos (por la izquierda) forman un número divisible por 2, el número formado por los tres primeros dígitos es divisible por 3, el formado por los cuatro primeros dígitos es divisible por 4, y así hasta que terminemos con los dígitos del número.
Por lo tanto, el número pandigital con cero 3.816.547.290 es polidivisible ya que 38 es divisible por 2 (38 : 2 = 19), 381 es divisible por 3 (381 : 3 = 127), 3.816 es divisible por 4 (3816 : 4 = 954), 38.165 es divisible por 5 (38.165 : 5 = 7.633), 381.654 es divisible por 6 (381.654 : 6 = 63.609), 3.816.547 es divisible por 7 (3.816.547 : 7 = 545.221), 38.165472 es divisible por 8 (38.165472 : 8 = 4.770.684), 381.654.729 es divisible por 9 (381.654.729 : 9 = 42.406.081) y 3.816.547.290 es divisible por 10 (3.816.547.290 : 10 = 3.816.547.29).

Por cierto, el número polidivisible más grande que existe tiene 25 dígitos y es el número 3.608.528.850.368.400.786.036.725.
D. El número pandigital restringido sin cero (respectivamente, con cero) más pequeño que es un cuadrado es 139.854.276 = 11.8262 (resp. 1.026.753.849 = 32.0432), mientras que el mayor es 923.187.456 = 30.3842 (resp. 9.814.072.356 = 99.0662), de un total de 30 (resp. 87) números pandigitales restingidos sin cero (resp. con cero) que existen.
La sucesión de los treinta números pandigitales restringidos sin cero que son cuadrados es la sucesión A036744 en la Enciclopedia On-line de Sucesiones de Números Enteros (139.854.276, 152.843.769, 157.326.849, 215.384.976, etc.), mientras que la sucesión A036745 es la formada por los ochenta y siete números pandigitales restringidos con cero que son cuadrados (1.026.753.849, 1.042.385.796, 1.098.524.736, 1.237.069.584, etc.).
E. El número 12.345.678.987.654.321 es un número pandigital redundante sin cero bastante curioso, ya que es capicúa (véase la entrada El secreto de los números que no querían ser simétricos), de hecho, el más pequeño posible entre los pandigitales sin cero, y cuadrado. Este número es igual al cuadrado del número formado únicamente por unos 111.111.111.
F. Potencias de 2 pandigitales.
Busquemos potencias de 2 que sean pandigitales. Si vamos analizando las diferentes potencias de 2, tenemos que hasta la potencia 27 no tenemos un número con nueve cifras (227 = 134.217.728), pero no es pandigital. De hecho, no existen potencias de 2 que sean números pandigitales restringuidos. La primera potencia de 2 que nos da un número pandigital redundante sin cero es 51, ya que 251 = 2.251.799.813.685.248, que claramente es pandigital. La siguiente es 67, que da lugar al número pandigital redundante sin cero 147.573.952.589.676.412.928. Existen cuatro potencias de dos más que nos dan números pandigitales redundantes sin cero, que son 72, 76, 81 y 86. Más aún, 86 es la potencia k más alta conocida para la que 2k no contiene la cifra 0 entre los dígitos de su expresión decimal. Es un problema abierto si existe otra potencia k con esta propiedad.
Por otro lado, la primera potencia de 2 que nos da un número pandigital redundante con cero es 68. En concreto, 268 = 295.147.905.179.352.825.856. Y van apareciendo cada vez más de estas potencias, 70, 79, 82, 84, 87, 88, 89, etc. hasta llegar a 167. Entonces, tenemos 168 que es la última potencia conocida para la que 2168 no es un número pandigital redundante con cero. De hecho, existe la conjetura de que todas las potencias 2k, con k mayor que 168, son pandigitales.

Rompecabezas numéricos pandigitales
Los números y expresiones numéricas pandigitales han formado parte de las revistas y libros de rompecabezas matemáticos desde hace muchísimo tiempo. A continuación, vamos a mostrar algunos ejemplos clásicos.
A. El siglo digital.
Un problema clásico de este estilo es el que aparece ligado a dos de los más grandes creadores de juegos lógicos y rompecabezas matemáticos, el estadounidense Sam Loyd (1841-1911) y el inglés Henry E. Dudeney (1857-1930), quienes colaboraron por correspondencia durante un tiempo, hasta que el inglés acusó al norteamericano de robarle sus rompecabezas y publicarlos con su nombre. El pasatiempo que vamos a incluir a continuación aparece con el nombre El siglo digital en el libro de Dudeney Diversiones matemáticas (1917) y en el libro de Loyd Cyclopedia de 5000 rompecabezas, trucos y acertijos con respuestas (1914), como El problema centenario.
El siglo digital: Con todas las cifras, del 1 al 9, en orden creciente, intercalar los signos «+» y «–» de forma que el resultado de la operación sea 100. Por ejemplo,
1 + 2 + 3 – 4 + 5 + 6 + 78 + 9 = 100.
Hay diez soluciones, aparte de la mostrada. Si el problema te atrae, intenta encontrar las quince soluciones del mismo problema, pero donde las cifras se colocan en orden decreciente.
Nota: También podrían considerarse otras operaciones como la multiplicación “x” o la división “:” y cualquier orden, no solo los órdenes creciente y decreciente.
Este es un problema muy sencillo que incluimos en las tarjetas de pasatiempos matemáticos del proyecto Marzo, Mes de las Matemáticas, del año 2021. Podéis verlo, con su solución, en la página web del proyecto marzomates.
B. Sumas pandigitales.
En general, este tipo de problemas son de la forma ABC + DEF = GHI, donde las letras corresponden a las nueve cifras básicas no nulas, del 1 al 9, o incluso, a nueve de las 10 cifras básicas, incluyendo el cero. También, puede tenerse la forma ABC + DEF = GHIK, con las diez cifras básicas.
De nuevo, encontramos los primeros ejemplos en los problemas del británico Henry E. Dudeney, en su libro Diversiones matemáticas / Amusements in mathematics (1917). El problema 79 con el título El rompecabezas de las taquillas, que fue originalmente publicado en la revista británica Tits-Bits, en 1897.
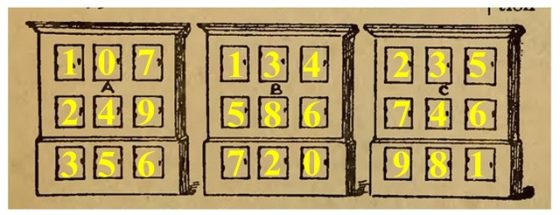
El rompecabezas de los casilleros: Un hombre tenía en su oficina tres armarios, cada uno de los cuales contenía nueve casilleros, como se muestra en el diagrama. Le dijo a su empleado que colocara un número de una cifra diferente en cada taquilla del armario A, y que hiciera lo mismo en el caso de B, y de C.
Ahora bien, el empresario no dijo que los armarios debían ser numerados en ningún orden numérico, y se sorprendió al encontrar, cuando el trabajo estaba hecho, que las cifras habían sido aparentemente mezcladas indiscriminadamente. Al pedirle explicaciones a su empleado, el excéntrico muchacho le dijo que se le había ocurrido ordenar las cifras de manera que en cada caso formaran una simple suma, las dos filas superiores de cifras producían la suma de la fila inferior. Pero el punto más sorprendente era éste: que los había dispuesto de tal manera que la suma en A daba la menor suma posible, que la suma en C daba la mayor suma posible, y que los nueve dígitos de los tres resultados totales de las sumas eran diferentes. El acertijo consiste en mostrar cómo se puede hacer esto. No se admiten decimales y el cero no puede aparecer en el lugar de la centena.
Es decir, nos está pidiendo que busquemos tres sumas del tipo ABC + DEF = GHI, como comentábamos al principio. La solución a este problema, aunque os animo a que la encontréis vosotros mismos, es la siguiente. La suma más pequeña de este tipo es 107 + 249 = 356 (que iría en el primer armario), mientras que la suma más grande es 235 + 746 = 981, o también, 324 + 657 = 981 (una de ellas iría en el tercer armario). Como los resultados de esas dos sumas son 356 y 981, entonces el resultado de la suma del armario del centro debe de tener tres de las cifras restantes, es decir, 0, 2, 4, 7. Por lo tanto, las sumas posibles para el armario del centro son 134 + 586 = 720, 134 + 568 = 702 ó 138 + 269 = 407.
En el mismo libro, Diversiones matemáticas (1917), Dudeney plantea otro interesante problema pandigital, el número 77, llamado dígitos y cuadrados.
Dígitos y cuadrados: Como se muestra en el siguiente diagrama, se han colocado las nueve cifras básicas en un cuadrado de manera que el número de la segunda fila es el doble que el de la primera fila, y el número de la fila inferior sea el triple del de la fila superior. Hay otras tres formas de ordenar los dígitos para obtener el mismo resultado. ¿Puedes encontrarlas?
Antes de comentar la solución a este rompecabezas pandigital, os animo, como siempre, a que os divirtáis buscando vosotras mismas las soluciones. En este problema nos están pidiendo que busquemos tres números, de tres dígitos, de manera que entre los tres tengan las nueve cifras básicas, del 1 al 9, que el segundo sea el doble del primero, que el tercero sea el triple del primero y que la suma de los dos primeros sea el tercero. Como puede verse en la anterior imagen, estas propiedades se cumplen para los tres números incluidos en ella, la terna (192, 384, 596): 192, 384 (= 192 x 2) y 596 (= 192 x 3), que entre los tres tienen las nueve cifras básicas y 192 + 384 = 596. Las otras tres soluciones por las que nos pregunta el rompecabezas son las ternas de números (219, 438, 657), (273, 546, 819) y (327, 654, 981). Una curiosidad más. Las cuatro ternas pueden dividirse en dos grupos de dos ternas, de manera que en cada uno de los dos grupos los tres números de una terna son anagramas (sus dígitos están escritos en otro orden) de los tres números de la otra terna: (192, 384, 596) y (219, 438, 657); (273, 546, 819) y (327, 654, 981).
Otro problema de este tipo aparece propuesto en el libro The Calculator Puzzle Book (1978), de Claude Birtwistle. Este rompecabezas, titulado Tres por tres, segunda parte, aunque con una escritura más literaria que la que proponemos aquí, nos plantea lo siguiente.
Tres por tres, segunda parte: Buscar tres números de tres dígitos ABC, DEF, GHI, que entre los tres tengan las nueve cifras básicas y tales que su suma y su producto sea la menor posible.
La solución sería la siguiente. Para empezar, pensemos en los tres números ABC, DEF y GHI que nos den la menor suma posible. Para ello, los dígitos de las centenas A, B, C deben ser lo más pequeños posibles, luego deberían ser 1, 2 y 3. Y razonando de la misma forma para decenas y unidades, tenemos que la suma más pequeña es 147 + 258 + 369 = 774. Aunque si permutamos el orden de los dígitos de cada posición (centenas, decenas, unidades) se obtiene la misma suma, por ejemplo, 347 + 158 + 269 = 774 ó 368 + 249 + 157 = 774. Como el orden de la suma y del producto no importa, podemos considerar que A = 1, B = 2 y C = 3, luego tendremos 62 = 36 grupos de tres números con tres dígitos cuya suma sea 774 para ver cuánto es su producto. De todos ellos, el menor producto corresponde precisamente a 147 x 258 x 369 = 13.994.694.

C. Productos pandigitales.
Si miramos la historia de los rompecabezas matemáticos relacionados con los productos pandigitales nos encontramos de nuevo a los dos grandes creadores de juegos lógicos y rompecabezas matemáticos mencionados, Sam Loyd y Henry E. Dudeney. Según el matemático estadounidense David Singmaster la primera aparición de un problema de este tipo fue en la revista Tits-Bits, en 1897. Era el problema Malabares con las cifras de Sam Loyd y se pedía encontrar un producto ABCD x E = FGHIJ, tal que esté formado por las diez cifras básicas, del 0 al 9, y el resultado del producto sea el menor posible. La solución a este problema es 3907 x 4 = 15.628. Además, si nos piden que el resultado sea el mayor posible la solución sería 9.403 x 7 = 65.821.
En el libro Los acertijos de Canterbury (1907) de Henry E. Dudeney nos encontramos también algunos rompecabezas de este tipo, como el siguiente (que había sido publicado en el London Magazine, en 1902).
El acertijo del molinero: El Molinero llevó luego a la compañía hacia un rincón y les mostró nueve sacos de harina, que estaban colocados como se ilustra en la figura.
“Ahora escuchad todos — les dijo—, pues os presentaré la adivinanza de los nueve sacos de harina. Y observad, caballeros y señores míos, que hay sólo un saco en cada extremo, cada cual seguido de un par, y tres sacos juntos en medio. Por San Benito, sucede que si multiplicamos el par 28 por su vecino, 7, el producto es 196, que ciertamente es la cifra que muestran los tres sacos del medio. Sin embargo, no es verdad que el otro par, 34, al ser multiplicado por el único saco en ese extremo, 5, resulte también 196. Por tanto, os ruego, gentiles señores, que recoloquéis los sacos con el menor trabajo posible, de tal forma que cada par, al ser multiplicado por su vecino, produzca el número del medio.” Ya que el Molinero ha estipulado, en efecto, que debe moverse la menor cantidad de bolsas posible, hay una sola respuesta a este acertijo, que todos deberían poder hallar.
El problema consiste en buscar el doble producto A x BC = DEF = GH x I formado por las nueve cifras básicas positivas, de 1 al 9, pero de forma que el número de movimientos de los sacos sea el menor posible. Si intentamos solucionar el problema aritmético A x BC = DEF = GH x I, tenemos las siguientes soluciones 2 x 78 = 156 = 39 x 4; 4 x 39 = 156 = 78 x 2; 3 x 58 = 174 = 29 x 6; 6 x 29 = 174 = 58 x 3. La que requiere menos movimientos de sacos es 2 x 78 = 156 = 39 x 4.
Otro rompecabezas en el mismo libro es Los bloques numerados, que dice así.
Los bloques numerados: Los niños de la ilustración han encontrado que se puede inventar una gran cantidad de acertijos muy interesantes e instructivos, a partir de cubos numerados; es decir, cubos que presenten los diez dígitos de las cifras arábigas —1, 2, 3, 4, 5, 6, 7, 8, 9 y 0―. El acertijo en particular con el que se han estado divirtiendo es dividir los bloques en dos grupos de cinco, y luego disponerlos en forma de dos multiplicaciones, en las que un producto sea igual al otro. El número posible de soluciones es muy considerable, pero ellos han dado con la disposición que da el menor producto posible. Así, 3.485 multiplicado por 2 es 6.970, y 6.970 multiplicado por 1 es lo mismo. Les resultará imposible conseguir un resultado menor.
Bien, mi acertijo consiste en hallar el mayor resultado posible. Dividan los cubos en dos grupos de cinco a gusto, y dispónganlos para formar dos multiplicaciones que resulten en el mismo producto y el más alto posible. Eso es todo, y sin embargo es un asunto que requiere bastante trabajo.
Por supuesto, no se permiten fracciones, ni tampoco trucos de ninguna especie. El acertijo es lo bastante interesante en la sencilla forma en que se los he dado. Quizás deba agregarse que los segundos factores pueden tener dos cifras.
En este caso, se busca solucionar el problema aritmético AB x CDE = FG x HIJ, utilizando las diez cifras básicas. La solución es 915 x 64 y 732 x 80, cuyo producto en ambos casos es 58.560
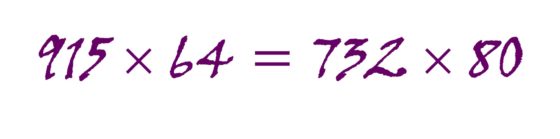
Podríamos contar mucho más sobre los rompecabezas de productos pandigitales y otros tipos de problemas de ingenio relacionados con las expresiones pandigitales, pero eso lo dejamos para otro día, que por hoy ya es suficiente.

Bibliografía:
1.- Raúl Ibáñez, La gran familia de los números, Catarata, 2021.
2.- Wolfram Mathworld: Pandigital number
3.- N. J. A. Sloane, Enciclopedia on-line de sucesiones de números enteros: oeis.org
4.- Wikipedia: Pandigital number
5.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1986.
6.- Henry E. Dudeney, Amusements in Mathematics, Thomas Nelson and sons,1917 (el original puede verse en la librería Internet Archive).
7.- David Singmaster, Sources in recreational mathematics, an annotated bibliography
8.- Henry E. Dudeney, Los acertijos de Canterbury y otros problemas curiosos, Granica, 1988.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

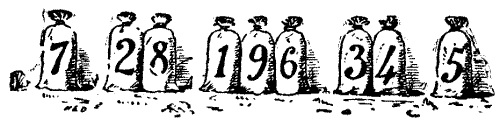

Universo pandigital — | Acusmata | Scoop…
[…] Un concepto sencillo, pero que da mucho juego, los números pandigitales, formados por todas las cifras básicas y cada cifra una única vez […]
Fracciones pandigitales — Cuaderno de Cultura Científica
[…] la anterior entrada del Cuaderno de Cultura Científica, titulada Universo pandigital, estuvimos hablando de números pandigitales, tanto de sus curiosas propiedades, como de algunos […]