Una serie clásica de novelas de ciencia ficción de la década de los años 1980 es La guía del autoestopista galáctico, del escritor inglés Douglas Adams (1952 – 2001). Originalmente fue una serie para la radio, de 1978, con ese mismo nombre. La serie literaria se compone de cinco libros, el primero que da título a toda la serie, La guía del autoestopista galáctico, fue publicado en 1979, al que siguieron El restaurante del fin del mundo; La vida, el universo y todo lo demás; Hasta luego, y gracias por el pescado e Informe sobre la Tierra.

En la novela aparece un superordenador, llamado Pensamiento Profundo y que es el segundo ordenador más grande del universo del espacio y del tiempo, que ha sido construido por una raza de seres “pan-dimensionales” que buscan el sentido de la vida. Cuando le preguntan al superordenador cuál es la “respuesta definitiva a la vida, el universo y todo lo demás”, éste contesta, después de siete millones y medio de años haciendo cálculos, que “cuarenta y dos”.
– Buenos días –dijo al fin Pensamiento Profundo.
– Hmmm… Buenos días, Pensamiento Profundo –dijo nerviosamente Loonquawl–, ¿tienes… hmmm, es decir…?
– ¿Una respuesta que daros? –le interrumpió Pensamiento Profundo en tono majestuoso–. Sí, la tengo.
Los dos hombres temblaron de expectación. Su espera no había sido en vano.
– ¿De veras existe? –jadeó Phouchg.
– Existe de veras –le confirmó Pensamiento Profundo.
– ¿A todo? ¿A la gran pregunta de la Vida, del Universo y del Todo?
– Sí.
Los dos hombres estaban listos para aquel momento, se habían preparado durante toda la vida; se les escogió al nacer para que presenciaran la respuesta, pero aun así jadeaban y se retorcían como criaturas nerviosas.
[…] Los dos hombres se agitaron inquietos. La tensión era insoportable.
– En serio, no os va a gustar –observó Pensamiento Profundo.
– ¡Dínosla!
– De acuerdo –dijo Pensamiento Profundo–. La Respuesta a la Gran Pregunta…
– ¡Sí…!
– … de la Vida, del Universo y de Todo… –dijo Pensamiento Profundo.
– ¡Sí…!
– Es… –dijo Pensamiento Profundo, haciendo una pausa.
– ¡Sí…!
– Es…
– ¡¡¡¿Sí…?!!!
– Cuarenta y dos –dijo Pensamiento Profundo, con calma y majestad infinitas.
Ante el asombro de sus creadores, el supercomputador les plantea que tienen que buscar cuál es la “pregunta definitiva”. Y como ese ordenador no puede contestar a esa pregunta construyen el superordenador más grande del universo, llamado Tierra, que es destruido antes de responder a la cuestión de cuál es la “pregunta definitiva” y se pierde la posibilidad de conocer esa información de vital importancia.
Esta historia de La guía del autoestopista galáctico es el motivo por el cual cuando hace unas semanas se pudo leer en la prensa que los matemáticos habían resuelto un problema relacionado con el número 42, a muchas personas nos vino a la cabeza la “respuesta definitiva a la vida, el universo y todo lo demás”.

Algunos de los titulares de prensa que pudieron leerse hace unas semanas fueron
“Matemáticos resuelven el diabólico acertijo del número 42, sin solución durante 65 años” (ABC Ciencia)
“Un viejo problema sobre el 42, resuelto” (Investigación y Ciencia)
“Resuelven por fin un misterioso problema matemático que lo puede cambiar todo” (El Confidencial)
Dejando la ciencia ficción a un lado, expliquemos cuál es el problema matemático al que se estaban refiriendo los titulares de la prensa. El problema es el siguiente.
Problema: ¿cómo expresar los números naturales del 1 al 100 como suma de tres cubos de números enteros?
Si lo escribimos de forma algebraica sería lo siguiente. Dado un número natural k, entre 1 y 100, buscar los números enteros x, y, z tales que verifican la ecuación diofántica:
x3 + y3 + z3 = k.
Empecemos explicando qué es una ecuación diofántica. Estas son ecuaciones polinómicas de dos o más variables x, y, z, etc, para las que se estudian las soluciones con números enteros (los naturales, el cero y los negativos).
Por ejemplo, se puede considerar la ecuación, en las variables x, y, z, relacionada con el teorema de Pitágoras x2 + y2 = z2 y estudiar sus soluciones enteras. Una solución de esta ecuación es la clásica (3, 4, 5), ya que 32 + 42 = 52. Estas soluciones enteras se conocen con el nombre de ternas pitagóricas. Otras ternas pitagóricas son (5, 12, 13) o (8, 15, 17). Los griegos se dedicaron a investigar la existencia de diferentes ternas pitagóricas. El matemático griego Diofanto, que vivió en Alejandría en el siglo III, escribió un libro sobre ecuaciones algebraicas de título Arithmetica. En particular, Diofanto elaboró una regla general para encontrar todas las ternas pitagóricas, y se interesó por el estudio de lo que hoy llamamos ecuaciones diofánticas.

Pero volviendo a nuestro problema, a la ecuación diofántica concreta x3 + y3 + z3 = k, o cómo expresar los números naturales del 1 al 100 como suma de tres cubos de números enteros, esta cuestión fue planteada de forma explícita y extensamente estudiada en un artículo publicado en 1955, en la revista Journal of the London Mathematical Society, por los matemáticos ingleses, J. C. P. Miller y M. F. C. Woollett, con el explícito título Solutions of the Diophantine Equation x3 + y3 + z3 = k.
Estos matemáticos se interesaron por este problema a raíz de un comentario del matemático inglés L. J. Mordell en otro artículo anterior, de 1953, en la misma revista:
“No sé absolutamente nada sobre las soluciones enteras de x3 + y3 + z3 = 3, más allá de la existencia de (1, 1, 1) y (4, 4, – 5); y tiene que ser realmente muy difícil descubrir algo sobre otras soluciones”.
Además, Mordell sugirió a sus colegas Miller y Woollett que utilicen el ordenador ERSAC, de la Universidad de Cambridge, para obtener soluciones de la ecuación diofántica x3 + y3 + z3 = k, para valores de k menores, o iguales, a 100. Fruto de ese trabajo es el mencionado artículo.
Aunque ya con anterioridad de había estudiado la ecuación x3 + y3 + z3 = k. En la revista inglesa de matemática recreativa The Ladies’ Diary se publicó en 1825, por S. Ryley, una familia de soluciones racionales, no enteras, de esa ecuación. Y las primeras soluciones enteras fueron obtenidas para las ecuaciones diofánticas x3 + y3 + z3 = 1 y x3 + y3 + z3 = 2 (k = 1, 2), en 1908 y 1936, respectivamente.

Pero volvamos a la ecuación diofántica x3 + y3 + z3 = k y al estudio de sus soluciones enteras.Veamos algunos ejemplos que nos permitan entender mejor la cuestión. Podríamos incluso plantearnos primero la ecuación x3 + y3 + z3 = 0, la cual por el último teorema de Fermat (véase la entrada Euler y el último teorema de Fermat) no tiene soluciones más allá de las triviales, del tipo (a)3 + (– a)3 + 03 = 0.
Para k = 1, además de la solución trivial 13 + 03 + 03 =1, se pueden encontrar otras soluciones, como 93 + (–8)3 + (–6)3 = 729 – 512 – 216 = 1 o (– 12)3 + 103 + 93 = –1728 + 1000 + 729 = 1. De hecho, en 1908 se demostró que existen infinitas formas de obtener 1 como suma de cubos, como aparece en el artículo de Miller y Woollett:
(9 t4)3 + (3 t – 9 t4)3 + (1 – 9 t3)3 = 1.
Este resultado se extiende, de forma natural, a los números que son cubos, a3. Luego, para números menores de 100 serían 8, 27 y 64.
También se probó, en 1936, que para k = 2, algunas de cuyas soluciones son 13 + 13 + 03 = 2 y 73 + (– 5)3 + (–6)3 = 2, existen, de nuevo, infinitas soluciones:
(6 t3 + 1)3 + (– 6 t3 + 1)3 + (– 6 t2)3 = 2,
que se extiende a los números que son el doble de un cubo, 2 a3. Para menores de 100 serían 16 y 54.
Para el 3, como menciona Mordell, se conocían solo las soluciones 13 + 13 + 13 = (– 5)3 + 43 + 43 = 3. A pesar de los intentos computacionales de encontrar más soluciones a esta ecuación diofántica x3 + y3 + z3 = 3, no se produjo ningún avance. Solo, en 1985, se demostró que una condición necesaria para que una terna de números enteros (x, y, z) fuese solución de esa ecuación debía de cumplir que x, y y z fuesen congruentes entre sí, módulo 9. Es decir, que el resto al dividirlos por 9 fuese el mismo. Pero ninguna solución particular fue encontrada.
Ahora tocaría el turno a los números 4 y 5. Aunque os recomiendo que no lo intentéis, puesto que no es posible. De hecho, el resultado es más general.
Proposición: No existen soluciones de la ecuación diofántica x3 + y3 + z3 = k, para valores de k “congruentes con 4 o 5, módulo 9”, es decir, que al dividirlos por 9 el resto de la división es 4 o 5, como los números 4, 5, 13, 14, 22, 23, 31, 32, 40, 41, 49, 50, 58, 59, 67, 68, 76, 77, 85, 86, 94 y 95.
Esto se debe a que cualquier número elevado al cubo a3 es congruente con 0, 1 u 8, módulo 9, es decir, el resto de dividir a3 entre 9 solo puede ser 0, 1 u 8. Por lo tanto, la suma de tres cubos no puede ser congruente con 4 o 5, módulo 9, puesto que no hay forma de sumar tres valores (pueden ser repetidos) de 0, 1 u 8 para que quede un resultado congruente con 4 o 5, módulo 9. Por ejemplo, los siguientes cubos 23 = 8, 33 = 27, 53 = 125, son congruentes con 8, 0 y 8, módulo 9, respectivamente, luego su suma es congruente con 8 + 0 + 8 = 16, es decir, congruente con 7, módulo 9. Efectivamente, 8 + 27 + 125 = 160 es congruente con 7, módulo 9, ya que al dividir 160 entre 9 nos queda 17 y de resto 7.

Los matemáticos británicos Miller y Woollett, utilizando el ordenador EDSAC, encontraron soluciones particulares para 69 valores de k entre 1 y 100, buscando en un rango de valores de x, y, z comprendidos entre – 3.164 y 3.164. Si tenemos en cuenta que además había 22 valores, menores que 100, para los que no existen soluciones, quedaron sin resolver las ecuaciones diofánticas correspondientes a nueve valores, a saber, 30, 33, 39, 42, 52, 74, 75, 84 y 87.
Llegados a este punto de esta entrada del Cuaderno de Cultura Científica, os animo a que os enfrentéis vosotros mismos a la búsqueda de soluciones particulares al problema de expresar los números naturales del 1 al 100 (evitad los nueve valores que no consiguieron resolver Miller y Woollett, así como los 22 valores que no tienen solución) como suma de tres cubos de números enteros. Para algunos valores de k no es difícil encontrar soluciones, mientras que para otros no es tan sencillo, aunque para la mayoría existen soluciones con x, y, z menores, en valor absoluto, que 25 (esto es, entre – 25 y 25). En particular, para k = 16 la solución de Miller y Woollett es complicada,
16263 + (– 1609)3 + (– 511)3 = 16.
Bueno, pues si os animáis, disfrutad del problema/juego… divertíos… pero no os olvidéis de seguir leyendo esta entrada.
A partir del artículo Solutions of the Diophantine Equation x3 + y3 + z3 = k, de J. C. P. Miller y M. F. C. Woollett, se empezó a trabajar en la solución de estos nueve números menores que 100 que quedaban pendientes, pero también se estudió la ecuación diofántica x3 + y3 + z3 = k, para valores de k mayores que 100, en particular, se puso mucho énfasis en los menores que 1.000. Para resolver estas ecuaciones diofánticas se desarrollaron nuevos algoritmos computacionales y se amplió el rango de valores para x, y, z.
Hasta el año 2001 se había resuelto el problema para todos los números menores que 100, salvo 33, 42 y 74, para los cuales se sabía que no existían soluciones para x, y, z menores (en valor absoluto) que 1011. Así mismo, se habían encontrado soluciones para las ecuaciones diofánticas de todos los valores menores de 1000, salvo veinte, además de los tres anteriores.
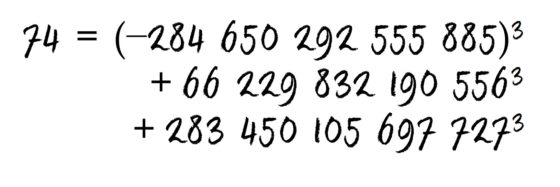
Hubo que esperar a 2016 para obtener una solución para el número 74 y al inicio de este año 2019, aún quedaban por resolver los números 33 y 42.
En abril de este año, 2019, el matemático británico Andrew Booker, de la Universidad de Bristol, empezó a trabajar en el problema de escribir el número 33 como suma de tres cubos a raíz del video The uncracked problem with 33 [https://www.youtube.com/watch?v=wymmCdLdPvM] del canal de Youtube Numberphile.
Booker desarrolló un nuevo algoritmo que le permitiera buscar soluciones enteras con números de 16 dígitos de la ecuación diofántica x3 + y3 + z3 = 33. Y, con ayuda de este algoritmo, encontró la buscada solución. Como cuenta el propio Andrew Booker en una entrevista para Numberphile, saltó de alegría en su despacho cuando encontró esa solución.

Y a principios del pasado mes de septiembre (de 2019) Andrew Brooker, junto con el matemático estadounidense Andrew Sutherland del MIT, han conseguido la solución del número que faltaba, el 42. Para ello han tenido que subir el rango de las posibles soluciones x, y, z a números de 17 dígitos. En concreto, el 42 se puede expresar como suma de tres cubos de la siguiente forma

Booker y Sutherland también encontraron algunas soluciones para números menores que 1000, como 165, 795 y 906. De esta forma ha quedado resuelto el problema, hasta los 100 primeros números, aunque hasta 1.000 aún quedan unos pocos… 114, 390, 579, 627, 633, 732, 921 y 975, sobre los que se seguirá trabajando en el diseño de algoritmos que los resuelvan.
Pero, ¡sorpresa! Solo diez días más tarde del anuncio de que habían conseguido resolver el problema de expresar el 42 como suma de tres cubos, Booker y Sutherland volvieron a hacer otro importante anuncio, relacionado con este problema. Por fin, habían encontrado una nueva solución de la ecuación diofántica citada por el matemático británico L. J. Mordell en 1953, x3 + y3 + z3 = 3, más allá de las ya conocidas (1, 1, 1) y (4, 4, – 5). Los números de esta solución no trivial tienen 21 dígitos.

Para resolver estos complicados problemas de computación, asociados a la solución de la ecuación diofántica, los matemáticos Andrew Booker y Andrew Sutherland utilizaron la aplicación Charity Engine, que conecta más de 500.000 ordenadores personales de todo el planeta, creando una red planetaria de ordenadores.
Existen muchos otros problemas que implican la suma de cubos de números, por ejemplo, el problema de ver qué números, en progresión aritmética, verifican que la suma de sus cubos es, de nuevo, un cubo. Por ejemplo, 33 + 43 + 53 = 63 (por cierto, que a este número, 63, se le conoce como el número de Platón) o 113 + 123 + 133 + 143 = 203, pero eso es otra historia que será contada en otra ocasión.

Bibliografía
1.- University of Bristol: Sum of three cubes for 42 finally solved
2.- Andrew R. Booker, Cracking the problem with 33, Res. Number Theory vol. 5, n. 29, 2019.
3.- John Pavlus, Sum-of-Three-Cubes Problem Solved for “Stubborn” number 33, Quanta Magazine, March, 2019.
4.- J. C. P. Miller y M. F. C. Woollett, Solutions of the Diophantine Equation x3 + y3 + z3 = k, Journal of the London Mathematical Society, vol. 30, pp. 101 – 110, 1955.
5.- L. J. Mordell, On the integer solutions of the equation x2+y2+z2+2xyz = n, Journal London Math. Soc, vol. 28, pp. 500-510, 1953.
6.- Armen Avagyan, Gurgen Dallakyan, A New Method in the Problem of Three Cubes, Universal Journal of Computational Mathematics vol. 5, n. 3, pp. 45-56, 2017.
7.- J. W. S. Cassels, A Note on the Diophantine Equation x3 + y3 + z3 = 3, Mathematics of Computation, vol. 44, n. 169, pp. 265-266, 1985.
8.- University of Bristol: Almost imposible 66-years-old maths puzzle solved
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Nota del editor: Como es costumbre en España se traduce el nombre del rey o la reina y su correspondiente consorte. También es correcto su título como «rey de Gran Bretaña»; la denominación «Gran Bretaña» para el estado duró desde el 1 de mayo de 1707 al 1 de enero de 1801, momento en el que pasó a ser «Reino Unido de la Gran Bretaña e Irlanda» («…Irlanda del Norte» desde 1927).
