Con esta entrada termina la serie Imago Mundi de la sección Matemoción del Cuaderno de Cultura Científica, que hemos dedicado a mostrar diferentes retratos del mundo, realizados con diferentes proyecciones cartográficas (matemáticas). En la primera entrega, ‘Imago mundi’, 7 retratos del mundo, las 7 proyecciones cartográficas utilizadas fueron: la proyección cilíndrica conforme de Mercator, la proyección pseudo-cilíndrica isoareal de Mollweide, la proyección pseudo-cilíndrica isoareal de Eckert IV, la proyección isoareal interrumpida homolosena de Goode, la proyección convencional de Van der Grinten, la proyección central, que preserva los caminos más cortos, y la proyección estereográfica, que es conforme.
Pero vayamos directamente a los retratos de esta tercera, y última, entrega de la serie.
Retrato 1: La proyección en perspectiva general
Si preguntáramos a la gente por la forma correcta de representar la superficie terrestre en un plano, muchas personas nos dirían que es realizando un retrato, o fotografía, desde un punto cualquiera del espacio. Esta es la conocida como proyección en perspectiva general.
La proyección en perspectiva general es una proyección geométrica azimuthal, que consiste en proyectar la superficie de la Tierra sobre un plano desde un punto de proyección mediante las rectas o “rayos” de proyección, es decir, como si estuviesemos mirando desde ese punto. Dependiendo de la posición del plano de proyección hablamos de perspectiva vertical o inclinada. La perspectiva es vertical si el plano es perpendicular a la recta que une el punto de proyección con el centro de la superficie terrestre, en otro caso, es inclinada.
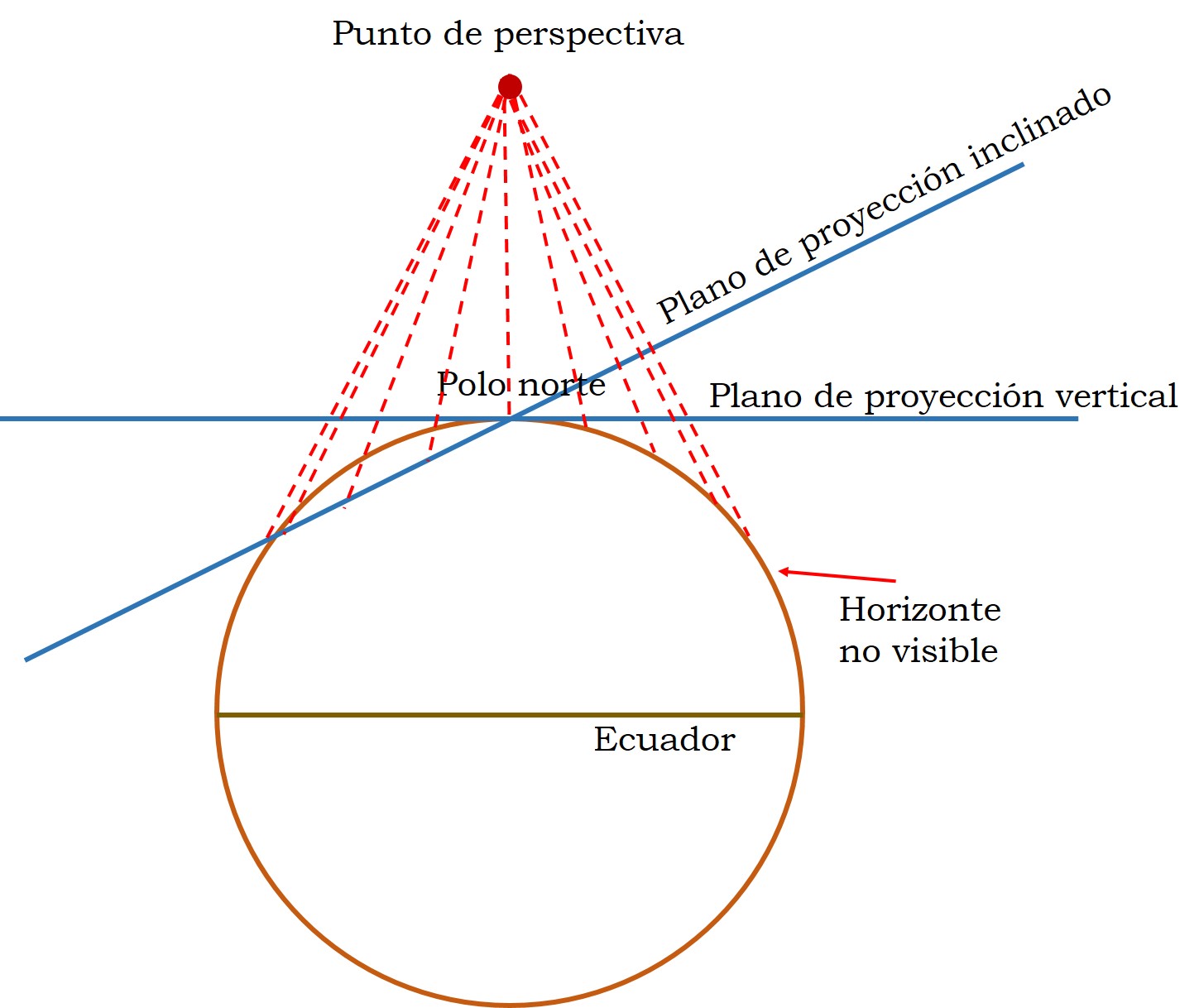
Dependiendo de lo lejos que esté el punto de proyección la imagen será más amplia o más reducida.

Pero estamos hablando de proyecciones matemáticas, y no de fotografía, por lo que podemos proyectar desde cualquier punto, incluso que esté en el interior del globo terrestre, y con el plano de proyección situado en cualquier posición, por ejemplo, en el lado opuesto, al punto de perspectiva, de la Tierra (lo que se llaman mapas en perspectiva vertical lejanos). Las proyecciones gnomónica, estereográfica y ortográfica (que veremos en el siguiente retrato) son casos particulares de la familia de proyecciones en perspectiva. Los siguientes diagramas nos muestran las diferentes opciones.
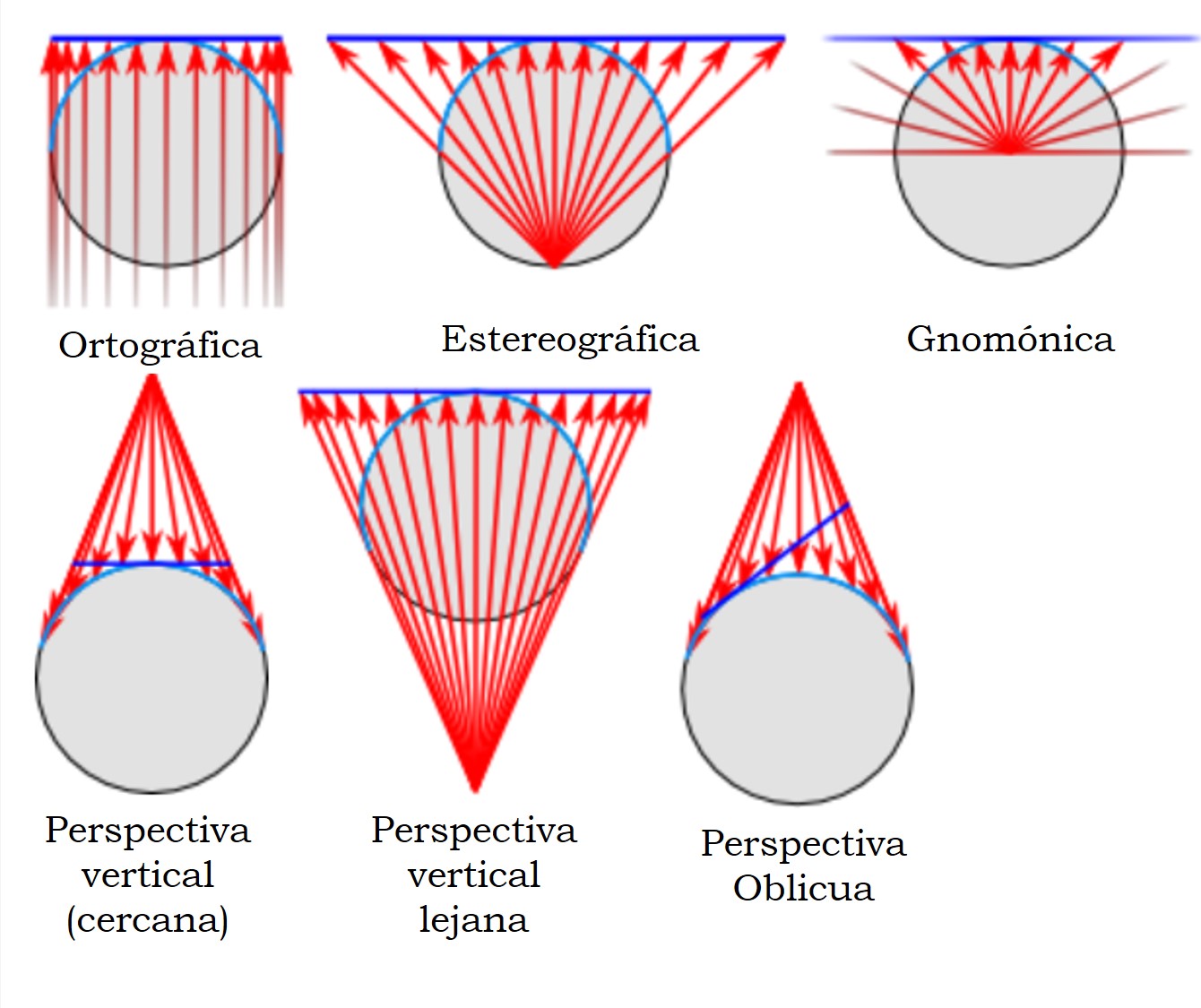
Mientras que las imágenes en perspectiva vertical general (con el plano cercano) nos muestran solo una parte de uno de los hemisferios, mediante el uso de un plano “lejano”, en la parte opuesta, de la superficie terrestre, al punto de proyección, se pueden obtener mapas que cubran más que un hemisferio.
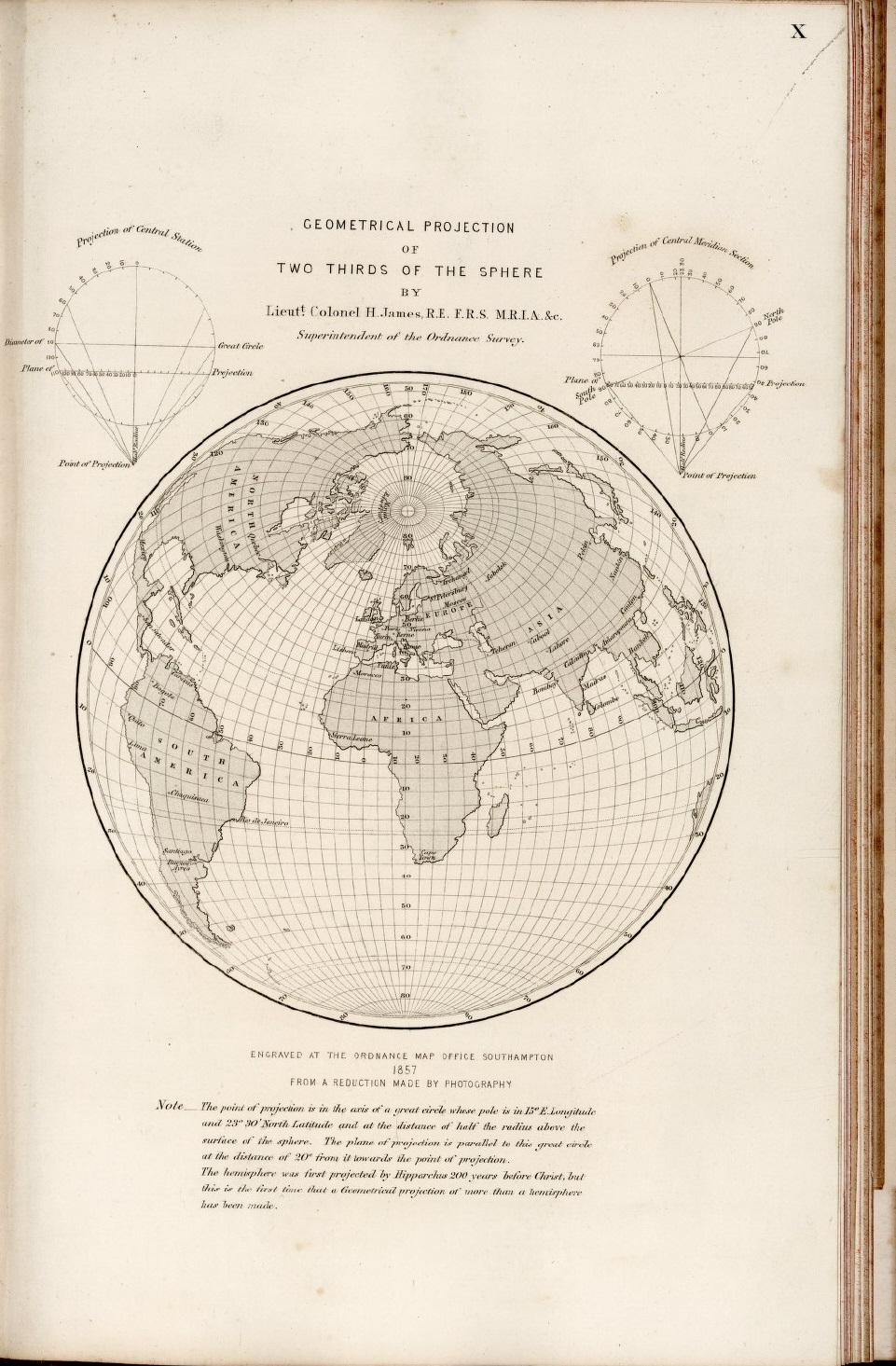
Por este motivo, la proyección en perspectiva vertical lejana fue utilizada por varios autores. El matemático francés Phillipe de La Hire (1640-1719) en 1701 con una distancia del punto de proyección de 1,7 veces el radio de la Tierra, desde el centro y en dirección opuesta al plano de proyección, el coronel británico Henry James (1803-1877), quien fuera director general de la agencia de mapas de Gran Bretaña, con una distancia de 1,5 veces el radio terrestre en 1857, el geodesta británico Alexander R. Clarke (1828-1914), junto con Henry James, a una distancia de 1,368 veces, en 1862, o solo, en su famosa “proyección crepúsculo”, con el plano a una distancia de 1,4 veces el radio de la Tierra, en 1879.
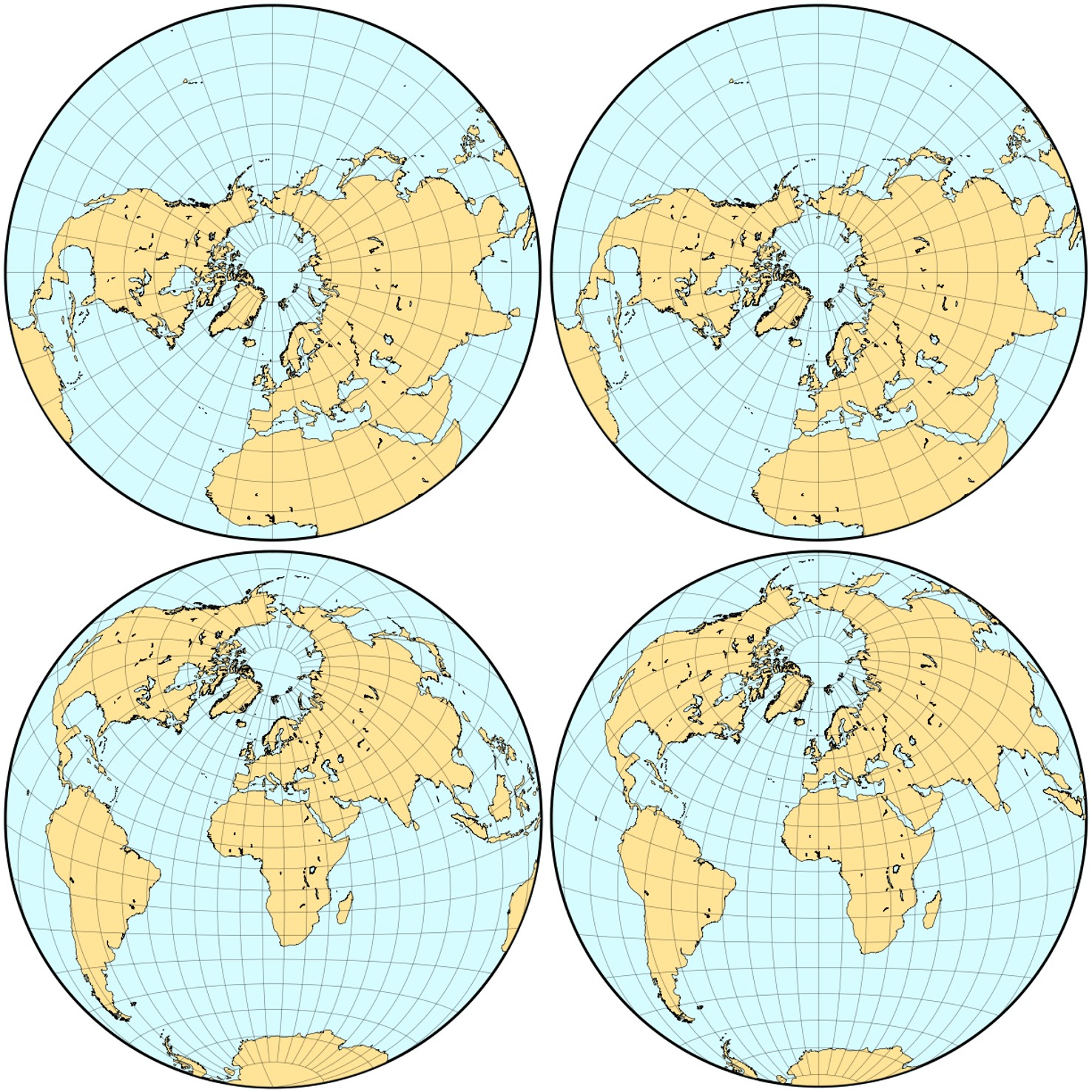
Retrato 2: La proyección ortográfica
La proyección en perspectiva es un caso particular de la anterior familia, si consideramos que el punto de proyección está lejos, en el infinito, luego los rayos de proyección van paralelos entre sí y perpendiculares al plano de proyección.

Esta proyección ya era conocida desde la antigüedad. Seguramente la era conocida por los egipcios y el matemático y astrónomo Hiparco de Nicea (aprox. 190-120 a.n.e.) la utilizó para sus cálculos de astronomía. En la antigüedad se conocía con el nombre de “analema”, que sería reemplazado por “ortográfica” en 1613, por el matemático francés Francois d’Aguillon (1567-1617). Aunque fue utilizada por primera vez para mapas del mundo en el siglo XVI, por el cartógrafo austriaco Johannes Stabius (1450-1522) y el artista renacentista alemán Alberto Durero (1471-1528).
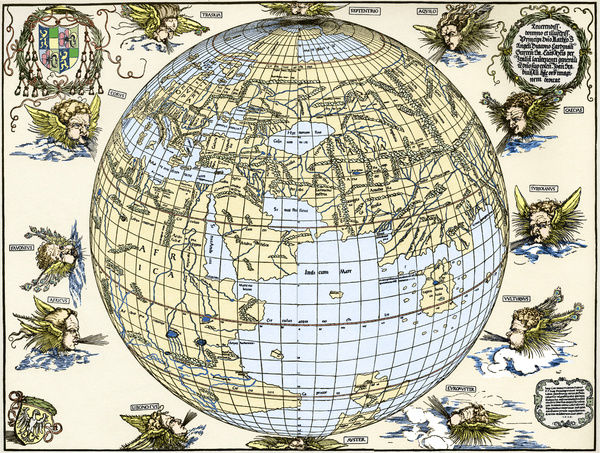
Esta proyección se suele utilizar por su aspecto similar al aspecto que tiene el planeta visto desde el espacio. No es una proyección que se haya utilizado en muchos atlas, pero sí en algunos, cuando se quiere mostrar la imagen de la Tierra desde el espacio exterior, como en The Global Atlas, A New View of the World from Space, publicado por Frank Debenham en 1958, en varios de los atlas de Rand McNally o por la US Geological Survey, USGS. Y volvió a utilizarse cuando empezó la carrera espacial.
Retrato 3: La proyección cónica conforme de Lambert
Tanto en las dos primeras entregas de esta serie de retratos del mundo, Imagi Mundi, como en los dos primeros retratos de esta tercera entrega, solamente hemos presentado proyecciones cilíndricas y acimutales, o generalizaciones de estas. Ahora vamos a presentar algunas proyecciones cónicas, es decir, cuya superficie auxiliar de proyección es el cono. Es decir, en el caso de las proyecciones geométricas, se proyecta primero la esfera terrestre básica sobre un cono, tangente (la intersección es una circunferencia, que será un paralelo en el caso normal, esto es, si el eje del cono coincide con el de la esfera terrestre básica) o secante (con dos circunferencias de intersección, que serán paralelos en el caso normal), a la esfera y luego este se despliega, cortando por una de sus rectas generadoras, en un plano.
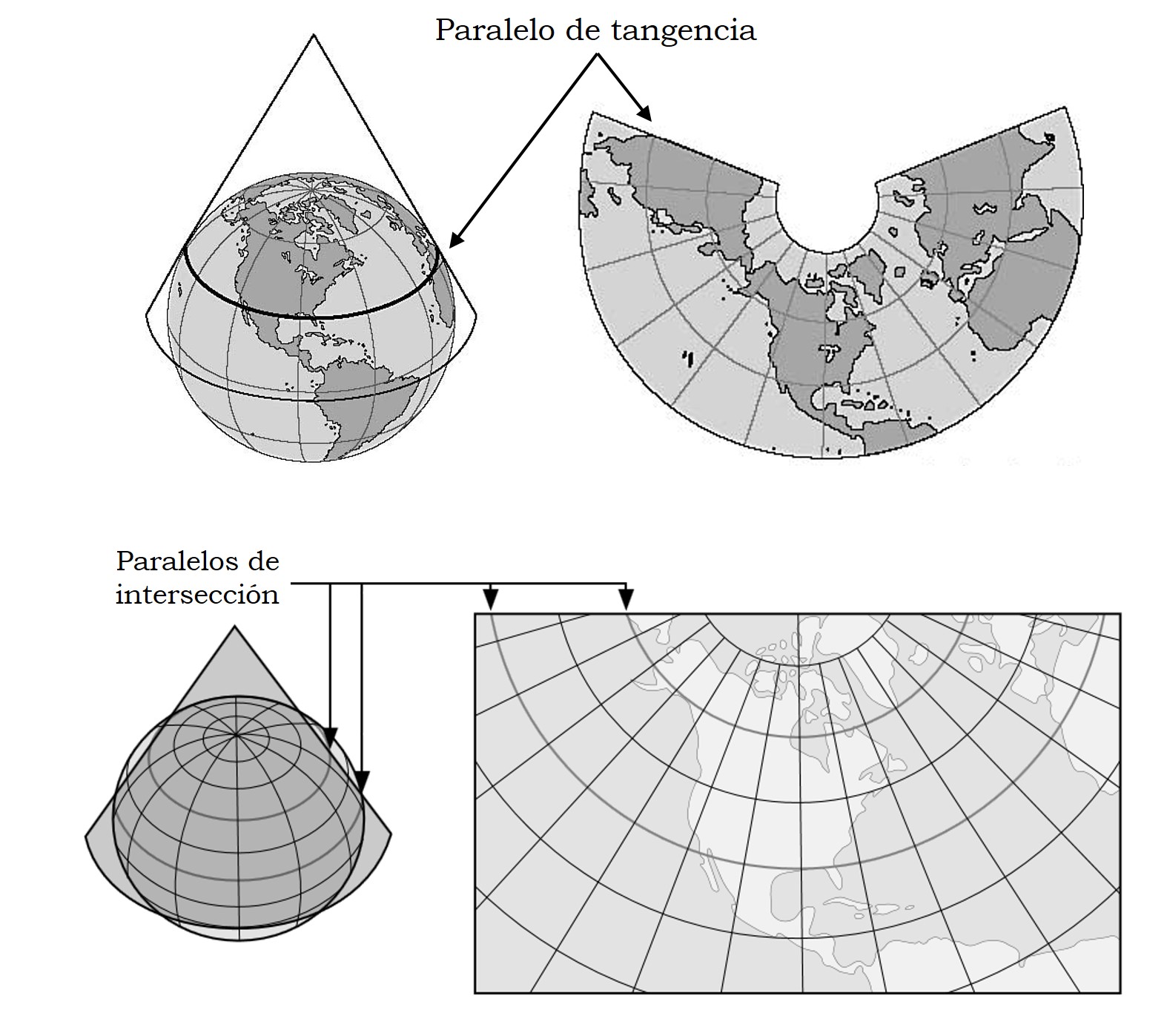
La proyección cónica conforme de Lambert es una de las siete proyecciones presentadas por el matemático alemán, aunque de origen francés, Johann H. Lambert (1728-1777) en su trabajo Notas y comentarios sobre la composición de mapas terrestres y celestes (1772). Lambert utilizó las herramientas matemáticas en su poder (cálculo, geometría, álgebra y trigonometría) para construir una familia de proyecciones conformes intermedias entre la proyección estereográfica (que es acimutal) y la proyección de Mercator (que es cilíndrica), para los casos tangentes (con un paralelo de tangencia) y secantes (con dos paralelos de intersección).
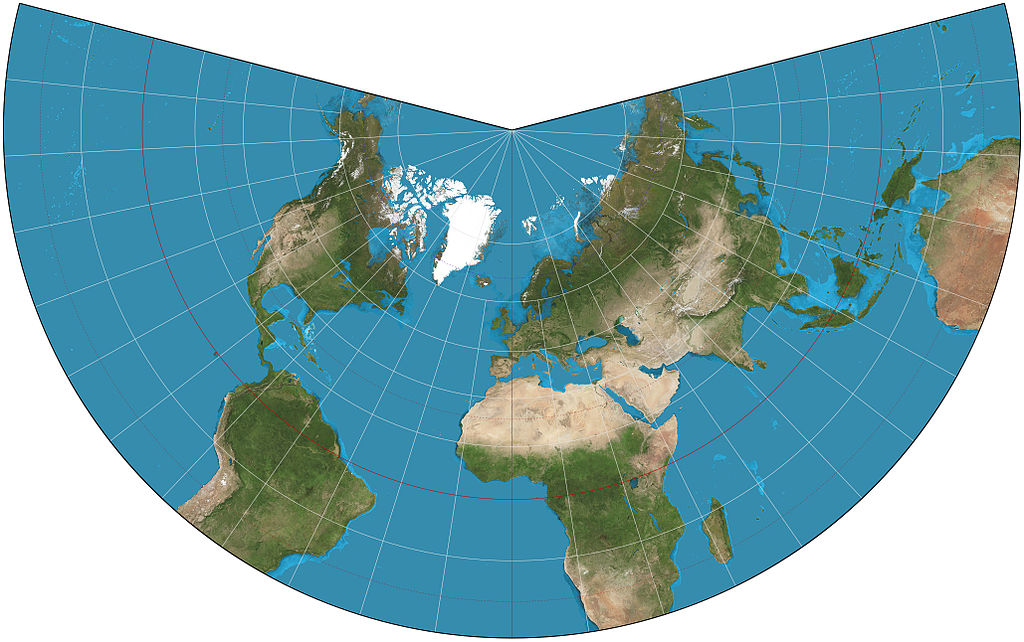
Como hemos comentado, esta proyección es conforme, preserva los ángulos, los rumbos, y para regiones pequeñas también las formas. La deformación es pequeña cerca de los paralelos de tangencia o intersección, y mayor al alejarse de ellos. Por este motivo, la proyección es muy útil para mapas de territorios en la dirección este-oeste, que se desarrollen alrededor del paralelo de tangencia o entre los dos paralelos de intersección, no estando estos muy alejados.
Hasta que fue utilizada por Francia durante la primera guerra mundial, esta proyección había permanecido olvidada. Después se ha convertido en una de las proyecciones más utilizadas para mapas de “escala grande” (esto es, es factor de proporcionalidad de la escala es pequeño), es decir, mapas de territorios pequeños. La utiliza la USGS de Estados Unidos, así como muchas otras agencias internacionales, para mapas topográficos. La Comisión Europea la recomienda para mapas conformes de Europa al completo de escalas mayores o iguales a 1:500.000 (como 1:100.000 o 1:25.000), y es común en países como Francia, Estados Unidos, Canada o México. También se emplea mucho para cartas náuticas.
Retrato 4: La proyección cónica isoareal de Albers
En su monografía de 1772, Johann Lambert también propuso una proyección cónica isoareal, que sería generalizada por el cartógrafo alemán Heinrich C. Albers (1773-1833) en 1805, también con uno o dos paralelos de intersección, que son aquellos en los que la escala es real (luego son llamados paralelos estándar). Como en el caso de la proyección cónica conforme de Lambert, los paralelos son arcos de circunferencias concéntricas y los meridianos son radios –rectas- de esas circunferencias igualmente espaciados, que cortan perpendicularmente a los paralelos. Los polos son arcos de circunferencia, el interior y el exterior, mientras que en la cónica conforme de Lambert era un punto (el norte o el sur, dependiendo de la versión), y el infinito.
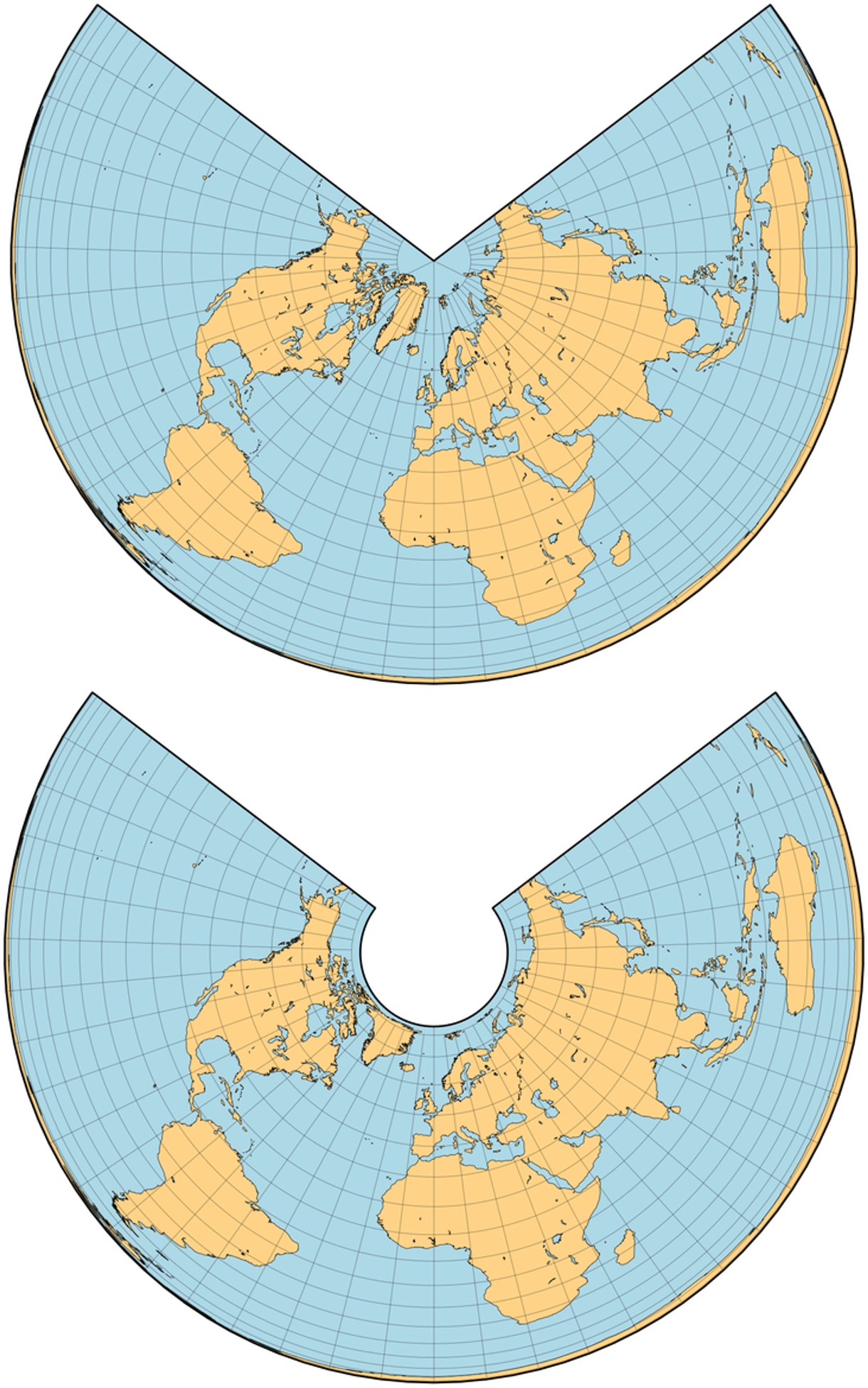
De nuevo, la deformación es pequeña cerca de los paralelos de tangencia o intersección, y mayor al alejarse de ellos, por lo que también es útil para mapas este-oeste. En particular, es una proyección, con deos paralelos estándar, muy utilizada para los mapas de Estados Unidos.
Retrato 5: La proyección de Bonne
En las proyecciones cónicas, ya sean geometricas puras o su generalización matemática, los meridianos (en la versión normal) se representan como radios (rectas), igualmente espaciados, de los arcos de circunferencias concéntricas que representan a los paralelos, mientras que en la generalización de estas proyecciones, las llamadas pseudo-cónicas, los meridianos siguen siendo arcos de circunferencia, mientras que los paralelos ya no son rectas.
Un ejemplo de proyección pseudo-cónica es la proyección de Bonne, que realmente es toda una familia de proyecciones pseudo-cónicas isoareales, en función de cual sea el paralelo estándar o central (correspondiente al paralelo de intersección con el cono).

El autor de esta familia de proyecciones fue el cartógrafo e ingeniero francés Rigobert Bonne (1727-1795). Aunque la proyección de Bonne ya había sido utilizada con anterioridad. Por ejemplo, en el mapa Universalis Cosmographia del cartógrafo alemán Martin Waldseemüller (1470-1520) de 1507 que modifica la segunda proyección de Ptolomeo o en su generalización en el mapa del mundo de Petrus Apianus de 1520, así como en el mapa del mundo del cartógrafo italiano Bernardo Sylvanus de 1511.


Los casos extremos son la proyección de Werner (o Stabius-Werner), cuando el paralelo estandar es 90ºN, que tiene forma de corazón y la proyección sinusoidal o de Sanson-Flamsteed, cuando el paralelo es 0º.
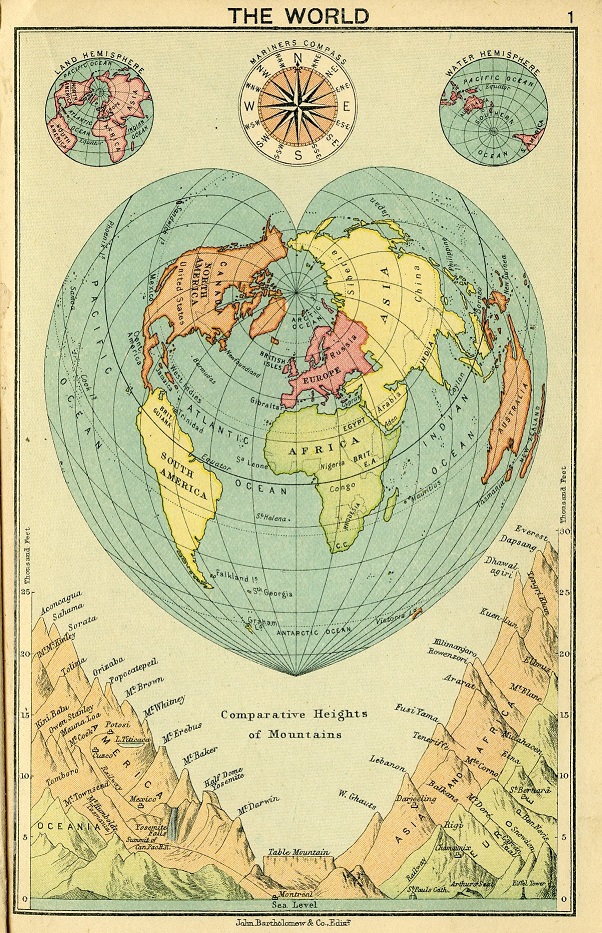
La proyección sinusoidal tiene este nombre ya que los meridianos son sinusoides, curvas de la función seno, mientras que los paralelos son rectas estándar, es decir, la escala es correcta a lo largo de los paralelos. Por este motivo, el mapa diseñado con la proyección sinusoidal se va encogiendo según los paralelos van acercándose a los polos, que son dos puntos. Para que la compresión no sea tan fuerte en los polos, se suele utilizar una versión cortada, o interrumpida.
Retrato 7: La proyección armadillo
Como ya hemos comentado, existen tres familias principales de proyecciones, en función de si la superficie auxiliar de proyección no existe (acimulates), es un cilindro (cilíndricas) o es un cono (cónicas). También se podrían tomar otras superficies auxiliares intermedias no necesariamente desarrollables, aunque no suele ser lo habitual, como en la proyección armadillo, desarrollada en 1943 por el cartógrafo estadounidense, de origen húngaro, Erwin J. Raisz (1893-1968), que consiste en proyectar la superficie terrestre básica sobre un toro (recordemos que en las matemáticas un “toro” es la superficie que tiene la forma de un flotador) y luego proyectar ortogonalmente, según una cierta dirección, en un plano.
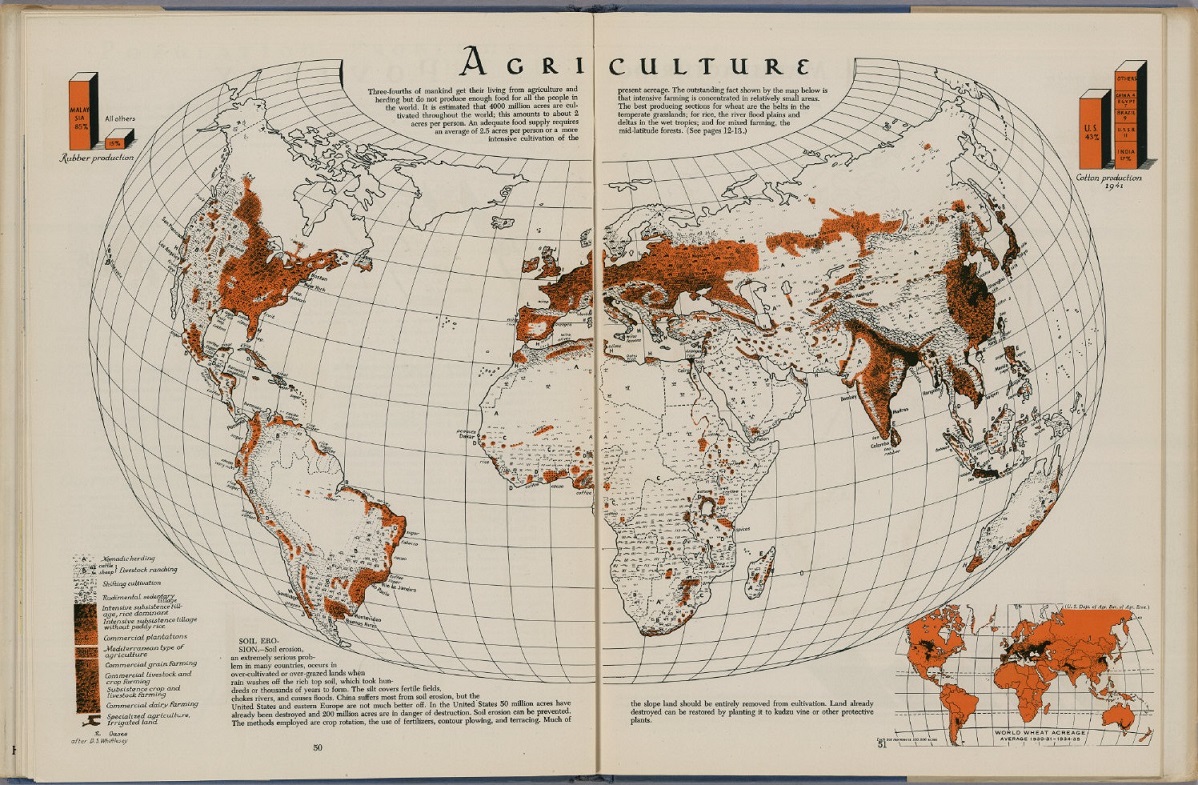
Retrato 8: La proyección globular de Nicolosi
Las proyecciones globulares son aquellas que pretenden representar la imagen esférica del globo terrestre, y contrariamente a las proyecciones acimutales, no son proyecciones geométricas, es decir, no están definidas a través de “rayos”, como ocurre en proyecciones acimutales como la gnomónica o la estereográfica, y en proyecciones cilíndricas como la proyección cilíndrica isoareal de Lambert. No preservan ni áreas, ni ángulos. Se limitan a un hemisferio, por lo que se necesitan dos mapas para cubrir toda la superficie terrestre.
Son proyecciones muy antiguas. Una de las proyecciones globulares más antiguas fue descrita por el filósofo inglés Roger Bacon (1214-1294) hacia 1265. La proyección globular conocida como de “Nicolosi”, que es una modificación de una proyección globular, la llamada primera, del jesuita, geógrafo y matemático francés Georges Fournier (1595-1652), fue realizada por el geógrafo italiano Giovanni Battista Nicolosi (1610-1670), aunque seguramente fue creada por el matemático persa Al-Biruni (973-1048).
En el mapamundi diseñado con la proyección globular de Nicolosi los meridianos y paralelos son circulares. De las proyecciones globulares, esta es la que produce menos distorsión en las formas. En la mayoría de los mapas modernos en los cuales se menciona que han sido diseñados con la proyección globular, se están refiriendo a la proyección globular de Nisolosi.
Retrato 9: La proyección regional de Bartholomew
En 1958 el cartógrafo escocés John C. Bartholomew (1923-2008) combinó la proyección cónica equidistante (esta una proyección cónica sencilla, donde los meridianos son rectas estándar, es decir, la escala es correcta a lo largo de los meridianos, igualmente espaciadas y los paralelos son arcos de circunferencia, igualmente espaciados, además, los dos paralelos de intersección con el cono son también curvas estándar), para latitudes por encima del Trópico de Cáncer (22,5ºN), y la proyección de Bonne interrumpida para el resto de la superficie terrestre.
Existen muchas más projecciones cartográficas, pero parafraseando al matemático británico Andrew Wiles, “creo que lo dejaré aquí”.

Bibliografía
1.- David Rumsey Map Collection
2.- National Geographic, Maps
3.- Raúl Ibáñez, El sueño del mapa perfecto; cartografía y matemáticas, RBA, 2010.
4.- Raúl Ibáñez, Muerte de un cartógrafo, Un paseo por la Geometría, UPV/EHU, 2002. Versión online en la sección textos-on-line de divulgamat
5.- J. P. Snyder, Flattening the Earth, Two Thousand Years of Map Projections, The University of Chicago Press, 1993.
6.- Carlos Furuti, Map projections
7.- J. P. Snyder, Map projections, A Working Manual, USGS Professional Paper 1395, 1987.
8.- Página web de la artista Joyce Kozloff
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Lurraren erradioaren historia – Zientzia Kaiera
[…] polimataren eskutik etorri zen. Baina Al-Biruni astronomo persiarrak garatu zuen metodo zehatzagoa. Al-Birunik ekuazio trigonometrikoak aplikatu zizkion mendi baten gailurraren eta haren oinetan kokatutako […]