A los científicos nos encanta ir reduciendo la multiplicidad del mundo observable a combinaciones de objetos más simples o a leyes más generales.

Con esta actitud hemos desarrollado explicaciones relativamente sencillas que dan cuenta de multitud de fenómenos de mucha mayor complejidad. Podríamos citar como ejemplos la tabla periódica o las ecuaciones de Maxwell.

Es preciso recordar que la naturaleza no tiene por qué ser simple ni elegante y que hay cierta complejidad con la que tenemos que lidiar, bastante agradecidos deberíamos estar de que se “deje” describir con las matemáticas.

Entre todos los científicos quizá los físicos seamos de los más recalcitrantes en esta actitud. Desearíamos que cualquier factor de una fórmula fuera una combinación de las constantes universales: c, ℏ, e… mientras que un ingeniero, que tiene que vérselas con el intransigente MundoRealTM, no tendrá mayores reparos en ir haciendo pruebas y ajustar su valor “a mano”, perdón, heurísticamente.

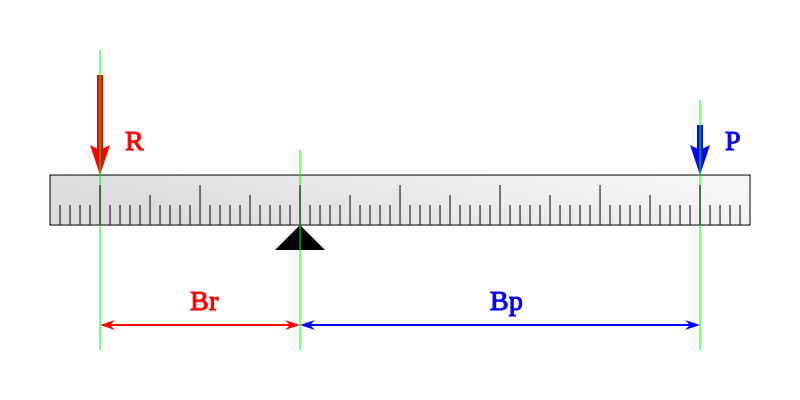
Con las fórmulas nos pasa algo parecido. Por ejemplo, la ley de la palanca, todo el mundo la conoce, todo el mundo la aplica (imagen de abajo). Muy bien, pero, ¿por qué? ¿De dónde sale eso? Cuando juntemos las fórmulas claves de la ciencia: las leyes de la termodinámica, las leyes de Newton… ¿habrá que hacerle un hueco a esta “ley de la palanca” que nadie sabe de dónde salió ni a quién debe pleitesía?

Pues no. Esta fórmula es fácilmente derivable de nuestra vieja amiga, la conservación de la energía que, como ya os contamos aquí, es de los asuntos que más claro vemos (aunque haya quien siga buscando un móvil perpetuo de primera especie y que Lisa Simpson lo tire por tierra con un proyecto escolar).

Nuestro objetivo en esta serie será derivar las fórmulas de los distintos mecanismos a partir de la conservación de la energía.

Como vamos a hablar de energía y trabajo quizá lo primero sería explicar cómo definimos el trabajo en física.

Para ser más precisos diremos “el trabajo que hace una fuerza”. Y dicho en palabras más sencillas sería: ¿Qué efecto ha producido esa fuerza en el sistema?

A ver qué os parece esta metáfora:

Tenéis una mina y un grupo de trabajadores que están con el mineral y las vagonetas. Miremos por la ventana.

Trabajador1: Está sentado tan tranquilo.

Trabajador2: Está empujando una vagoneta y esta se mueve en el sentido que está siendo empujada.

Trabajador3: Está empujando una vagoneta que se mueve por unos raíles, pero el tipo la empuja perpendicularmente al movimiento.

Trabajador4: Mientras dos trabajadores empujan una vagoneta en un sentido, nuestro amigo empuja en sentido contrario.

Volvamos a nuestra oficina y vayamos pensando en las nóminas de este mes.

El trabajador número uno, cuya fuerza es cero, supongo que no esperará ningún pago. Podríamos decir en lenguaje común que el trabajo ha sido cero.

El trabajador número dos sí que parece que nos esté aportando algún efecto, algún trabajo. La vagoneta se mueve y tiene que ver con la fuerza que está recibiendo. Muy bien. De hecho, si empujase con más fuerza o la vagoneta se moviese más distancia, me plantearía pagarle más.

El trabajador número 3 suda como un pollo, el pobre, pero no me aporta nada, la fuerza que él hace no tiene un efecto sobre el resultado que vemos. Lo siento, pero no cobrará, trabajo = cero.

El trabajador número cuatro me va a oír cuando acabe el día. No sólo no está aportando, sino que está dificultando, no diré que no tiene un efecto sobre el sistema, sí que lo tiene: negativo. Así que, bien podría pedirle yo dinero, en lugar de dárselo.

Escribamos esto como una ecuación:

El trabajo (el efecto) es directamente proporcional a la fuerza que se hace, a la distancia que se recorre… pero resulta importante el ángulo con el que se hace. Siendo lo más favorable estar alineado y apuntar en el mismo sentido, de influencia cero si se está perpendicular y negativo si se aplica la fuerza en sentido contrario al movimiento. Esto matemáticamente queda bien definido de la siguiente manera:

W = F · d · cos ɸ

W: Trabajo

F: Fuerza

d: distancia

ɸ: ángulo entre la fuerza y el desplazamiento.

La función coseno nos selecciona esa “parte” de la fuerza que está alineada con el desplazamiento y nos dará el valor negativo si va en sentido contrario.

Por lo tanto, si fuerza y desplazamientos están alineados y van en el mismo sentido, tendremos:

W = F · d

En la próxima entrega hablaremos de conservación de la energía y cómo aplicar estos argumentos a la obtención de la ley de la palanca.

Sobre el autor: Javier Fernández Panadero es físico y profesor de secundaria además de escritor de libros de divulgación.