En las entregas anteriores vimos cómo se definía el trabajo mecánico en física y cómo podía usarse la conservación de la energía para deducir la “ley de la palanca”.

En esta última entrega seguiremos el mismo procedimiento que en la anterior para derivar las “leyes” de otros mecanismos para mostrar cómo no son “leyes extra” de la física, sino el producto de la aplicación de la conservación de la energía.

Recordamos la técnica que usamos para la palanca:

• Asumimos que no hay pérdidas de energía (rozamiento u otras)

• Con argumentos geométricos vemos la diferencia de movimiento a la entrada y a la salida

• Aplicando que el trabajo (la energía) debe ser igual en ambos extremos, obtenemos la variación en las fuerzas

Plano inclinado

Aunque no os parezca un mecanismo, es un dispositivo que me permite variar fuerza y distancia para ejercer un trabajo mecánico, así que, ahí va.

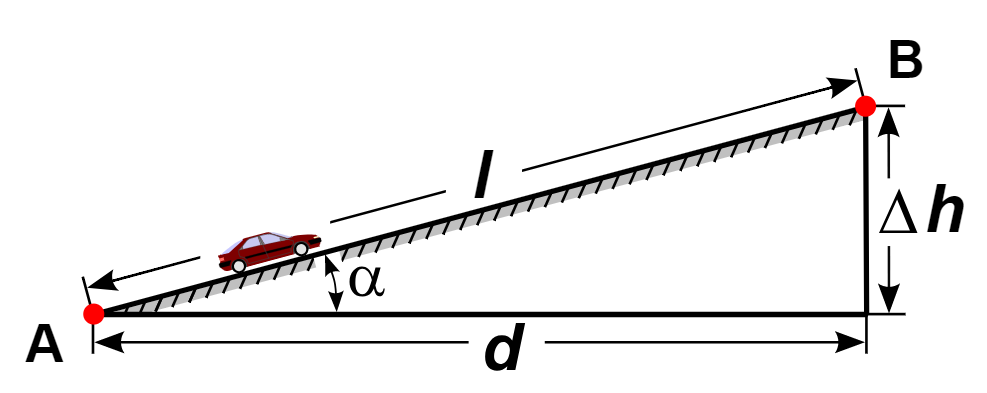
El objetivo es subir un objeto una determinada altura, bien puede ser el coche del dibujo, una caja que arrastremos, el carro de la compra. Aquello va a subir una altura Δh y podría hacerlo por dos caminos: directamente en vertical, desde la esquina inferior derecha hasta el punto B, o por la rampa, desde A hasta B.

Vayamos con nuestra técnica.

1. No tenemos en cuenta el rozamiento

2. Por geometría miremos la diferencia de camino recorrido

3. Por conservación de la energía estimamos la relación entre las fuerzas.

Llamemos 1 al trayecto por la rampa y 2 al trayecto vertical. En cualquier caso W₁ = W_2.

En el trayecto vertical la fuerza mínima que deberemos ejercer para elevar el objeto será el peso y la distancia Δh, la fuerza para movernos por la rampa no la sabemos, pero la distancia será L.

Recordamos una vez más que W = Fuerza·desplazamiento (si ambos alineadas)

F₁ · despl₁ = F₂ · despl₂

F₁ · L = Peso · Δh

F₁ = Peso · (Δh/L)

Resuelto. La fuerza que tengo que hacer es el peso multiplicado por un número que es menor que uno (fíjate que en un triángulo rectángulo así dispuesto, la altura siempre será menor que la rampa), por lo que la fuerza a hacer será una fracción del peso.

Cuanto menor sea la inclinación de la rampa o, si queréis verlo en función de d, cuanto mayor sea el desplazamiento horizontal de la rampa, menos fuerza tendré que hacer, pero más recorrido tendré que efectuar.

Para aquellos de vosotros que sepáis trigonometría, será claro que el factor reductor de la fuerza es el seno del ángulo alfa.

Vemos una vez más, que siempre tengo que “pagar” la misma energía. Estos sistemas nos permiten hacerlo a “plazos”, hago menos fuerza, pero tengo que ejercerla a lo largo de más distancia.

Tornillo

Este muchachito está muy infravalorado. Cuando decimos “tornillo” pensamos inmediatamente en esa pequeña punta con rosca que usamos para unir piezas, pero no es sólo eso, es el alma del tornillo de banco, los gatos de los carpinteros, algunos cascanueces (en realidad muchas herramientas de apriete), los sacacorchos y el gato con el que subimos el coche (¡de más de mil kilos!) usando una sola mano… deberíais gritar de asombro sólo con oír la palabra “¡Tornillo!”.

Un tornillo avanza linealmente cuando se le hace girar. Pueden ser a “derechas o izquierdas” según el sentido de giro para que avance, pero en ambos casos (y os lo pongo grande para que os lo imaginéis mejor) ¿no se trata realmente de un plano inclinado “enroscado” en un cilindro? Imaginaos subiendo por ahí.

Los tornillos a veces tienen más de un filete (la rampa), decimos que tienen varias entradas, lo veréis mejor en la siguiente imagen.

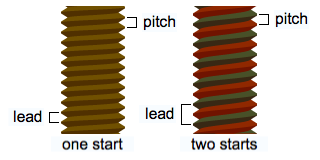
Miremos el primer caso (una entrada), hay sólo una escalera, perdón, un filete, y cada vuelta que damos subimos una altura que coincide con la distancia entre roscas, que llamamos paso (pitch).

En el segundo caso (dos entradas), hay dos rampas que no se “mezclan”. Piensa en que son dos escaleras, la gris empieza en el primer piso y al cabo de una vuelta te deja acceder al tercer (!) piso, mientras que la roja va pasando por los pisos pares.

Ya sabes que a los que nos gustan las funciones de estado, como las energías, nos importan poco los caminos (bromas de físico, no se enfanden). Lo que me preocupa a mí es cuánto avanzo en cada vuelta que haga dar al tornillo con mi destornillador o manivela.

Pongamos un ejemplo viejuno

Imaginemos que la varilla está roscada y llamemos D a la distancia desde el eje al mango.

Vayamos a nuestra técnica

W₁ = W₂

F₁ · despl₁ = F₂ · despl₂

El desplazamiento de la manivela para una vuelta será la longitud de la circunferencia 2?D.

El desplazamiento lineal del tornillo será el paso si es de una sola entrada y el paso por el número de entradas si es de varias entradas. Digamos que el paso es P y el número de entradas N

F₁ · 2?D = F₂ · P · N

F₁= F₂ (P · N / 2?D)

Hecho. La fuerza que tenemos que hacer en la manivela será distinta a la que hace el tornillo al “empujar” linealmente. Y se hará cada más pequeña cuanto menor sea el factor entre paréntesis, así que cuanto menor sea el paso y cuanto mayor sea la longitud de la manivela, menos fuerza tendremos que hacer. Fíjate que es de nuevo nuestro viejo lema, cuanto más nos movamos nosotros a un lado y menos se mueva la salida al otro, menos fuerza nos pide y más fuerza produce a la salida.

Polea y polipastos

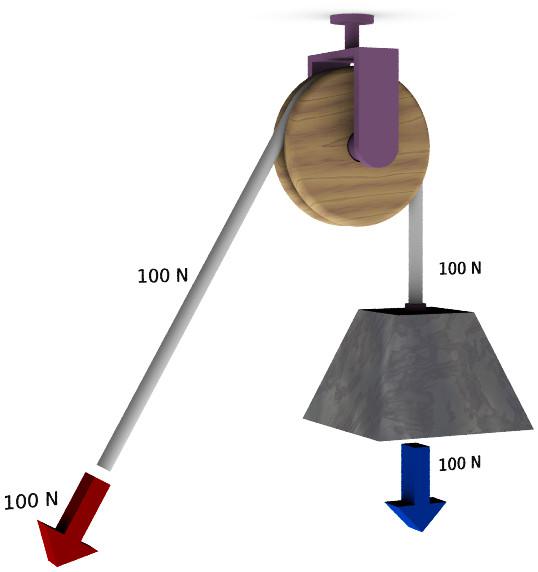
Este mecanismo antiquísimo, la polea, compañera de pozos en todo el mundo, nos permite cambiar la dirección de la fuerza que aplicamos para poder tirar hacia abajo, algo mucho más cómodo, pero, como veis en el dibujo, no consigue multiplicar nuestra fuerza. A estas alturas ya sabéis por qué: Cada metro que tiremos de cuerda hará subir el peso un metro y, si no hay cambio en el desplazamiento, no hay multiplicación de fuerzas.

Pero nadie nos impide usar más de una polea y hacer que unas estén fijas y otras móviles, lo que llamamos, polipastos.

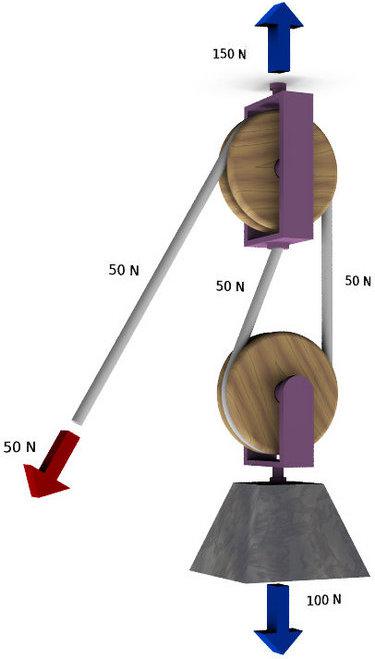
Mirémoslo mejor en este diagrama

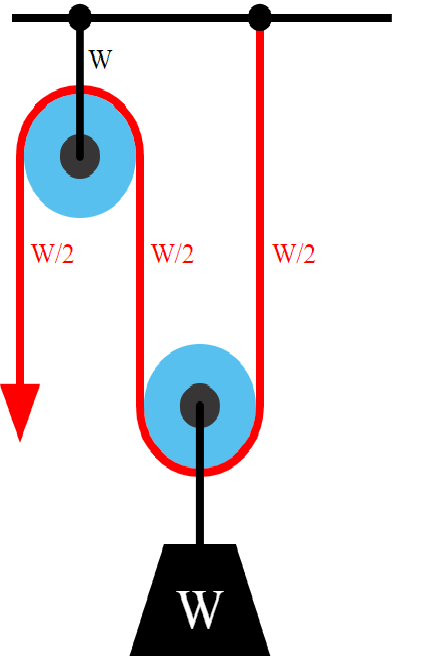
Cuando tiremos de la cuerda por el lado de la flecha la polea de la derecha subirá y con ella el peso. Aquí el fenómeno clave es que si recojo un metro de cuerda, esa distancia tendrá que repartirse entre las dos partes de cuerda a la derecha, de forma que el peso sólo subirá medio metro. Y aquí ya tenemos nuestro viejo truco en marcha.

W₁ = W₂

F₁ · despl₁ = F₂ · despl₂

F₁ · D₁ = F₂ · (D₁/2)

F₁ = F₂ · (½)

Así que, en el lado izquierdo hago la mitad de fuerza que en el lado derecho.

Si tenéis necesidad de más, podéis seguir añadiendo poleas, tendréis que pagar el precio de tener que recoger mucha más cuerda que el avance que obtengáis en el otro extremo (tantas veces más como tramos de cuerda tengáis para repartir la cuerda recogida), pero multiplicaréis enormemente vuestra fuerza. Como se hace en los barcos desde antaño

Para demostraciones del polipasto os aconsejo usar un par de palos y una cuerda como podéis ver en este vídeo (min:24:40) con la colaboración de los compañeros Iris y Andrés

Poleas y correas

Otro viejo conocido. Una rueda gira impulsada por un motor, el aire, un borrico, un señor… arrastra la correa que produce el movimiento de la otra rueda.

Vayamos a nuestros argumentos geométricos, la correa circula por el exterior de la polea, así que recorre la longitud de la circunferencia, pero, ¡los perímetros de las ruedas son diferentes!

Por cada vuelta que dé la polea grande, se “envía” un trozo de correa que la pequeña debe recoger y como cada vuelta de esta última tiene menos longitud, tendrá que dar más de una vuelta para recoger toda la correa enviada, tendrá que girar más rápido.

Vayamos a lo nuestro.

W₁ = W₂

F₁ · despl₁ = F₂ · despl₂

Si llamamos r al radio de la polea pequeña y R al de la polea grande.

F₁ · 2?r = F₂ · 2?R

F₁ = F₂ · (R/r)

Listo. Si la polea tiene la mitad de radio girará el doble de rápido, si tres veces más radio, tres veces más rápido.

Qué polea eliges como “motora” o como “conducida” será cuestión de para qué estés considerando usar el mecanismo.

Si lo que tienes es un motor que gira a toda pastilla y tú estás pensando en que las ruedas de un vehículo pesado, tendrás que reducir la velocidad y aumentar la fuerza.

Si lo que deseas es algo que se mueva muy rápido y no necesitas mucha fuerza para que se mueva, entonces puedes utilizar la polea mayor como “inicial” o conductora y la otra como conducida. En tecnología no es habitual hablar de bueno o malo, sino de adecuado o inadecuado, y eso depende fuertemente del contexto, esto es, de la aplicación.

Es interesante notar que la correa no participa en la “multiplicación” es un mero transmisor del movimiento, de hecho, si los ejes están próximos, este mecanismo se puede hacer sin correa con ruedas de fricción.

Engranajes

Para este mecanismo podríamos hacer la misma consideración sobre los diámetros que hicimos para las poleas y correas, pero con frecuencia los engranajes se caracterizan por el número de dientes.

Antes de esto hay que señalar que sólo engranan ruedas que tengan el mismo módulo, magnitud que nos da una idea del tamaño del diente. Por lo tanto, decir que sólo engranan ruedas dentadas del mismo módulo es decir que sólo engranan ruedas cuyos dientes sean del mismo tamaño… casi una obviedad.

Si en ambos engranajes tenemos los dientes del mismo tamaño podemos ver que cabrán más dientes si la longitud de la circunferencia (donde se disponen) es mayor, luego el número de dientes es proporcional a la longitud de la circunferencia.

Así que un engranaje con 24 dientes tiene tres veces más longitud de circunferencia que un engranaje de 8 dientes y, por lo tanto, tendrá que girar tres veces más lento.

Nota: Para los más avanzados en estos temas estoy hablando, evidentemente, de circunferencias y diámetros primitivos.

Engranajes y cadenas

En este mecanismo haríamos las mismas consideraciones que en los engranajes, la cadena es simplemente la manera de conectar dos engranajes alejados.

Os animo a que os hagáis las cuentas con los platos y piñones de vuestra bicicleta.

Tampoco hay diferencia cuando usamos correas de caucho dentadas a lo que las velocidades y las fuerzas se refiere, el uso de estos dispositivos tiene que ver con sistemas que tienen solicitaciones complicadas en esfuerzos y podrían deslizar si usasen correas o fricción. Estos “dientes” lo impiden.

Tren de engranajes

Como hemos visto el cambio de velocidad es tan sencillo en engranajes como hacer ruedas de distinto tamaño… pero en la práctica puede no ser tan sencillo. Por ejemplo, si quiero reducir la velocidad diez veces, tengo que hacer una rueda diez veces mayor. Es inviable.

Para esto aplicamos sucesivas reducciones usando varios ejes.

Hay una reducción entre las ruedas rojas y azul.

La rueda amarilla gira unida al mismo eje que la azul, así que a la misma velocidad.

Hay otra reducción entre las ruedas amarilla y verde.

Contando el número de dientes en cada rueda podrás calcular de qué magnitud es el cambio y, mirando la animación, comprobar tu predicción.

Así conseguimos mayores reducciones de velocidad en un espacio más pequeño que con sólo dos ejes.

Este sistema es el que se usa en las cajas de cambio de los vehículos, en los que constantemente cambiamos de marcha para tener menor velocidad y más fuerza o mayor velocidad y menos fuerza. Según las ruedas que engranes la transformación será diferente, y si metes un engranaje entre los ejes (R) cambiarás el sentido de giro e irás… ¡marcha atrás!

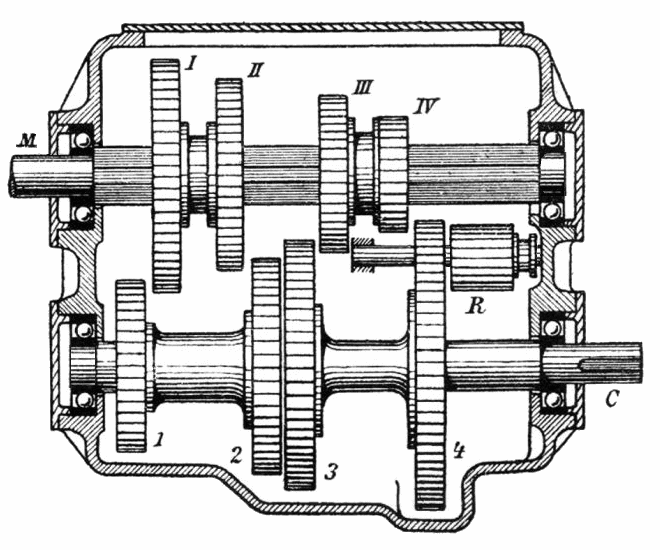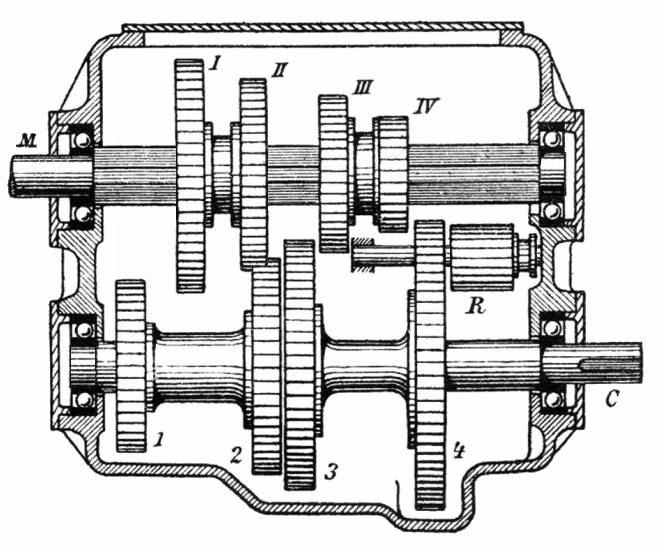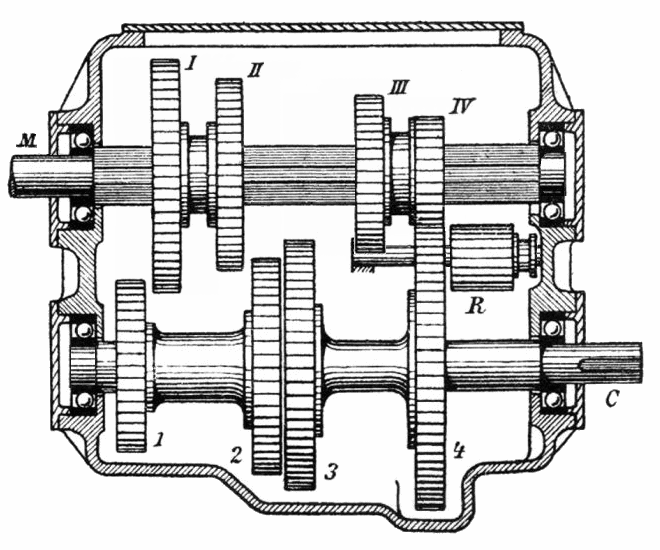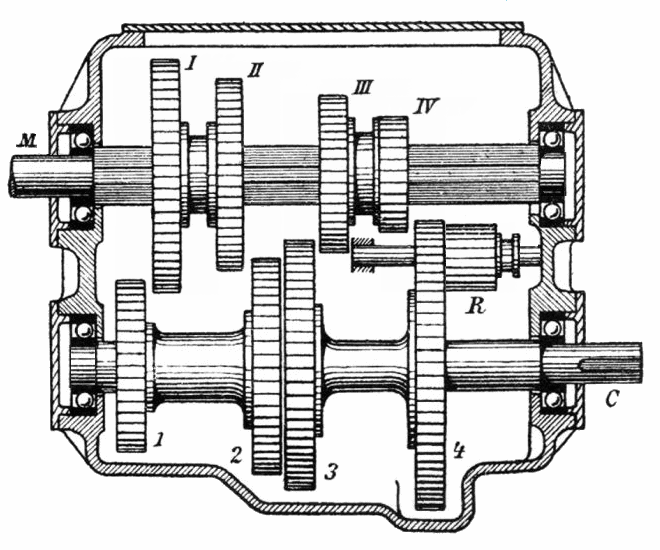
La demostración de que incluir un engranaje intermedio para cambiar el sentido de giro (engranaje loco) no influye en la velocidad final, os la dejo como ejercicio.

Tornillo sin fin y piñón

El tren de engranajes es algo muy interesante, pero si necesitamos aún mayores relaciones de transmisión, incluso eso se nos queda corto.

Aquí viene en nuestra ayuda el sin fin y piñón.

Por cada vuelta del tornillo el engranaje inferior sólo avanza… un diente.

De forma que si el piñón tiene 60 dientes, la velocidad se reduce SESENTA VECES y la fuerza aumenta en la misma proporción.

Muy usado en grúas, porque como curiosidad también os diré que si se construyen de la forma adecuada, cuando paras el tornillo, el mecanismo se queda bloqueado (no se pone a girar en sentido contrario) y la carga no se cae.

Y muchos más…

Podríamos seguir con otros muchos mecanismos, piñón y cremallera, torno, mecanismos articulados… pero creo que las ideas están muy claras y aquí os dejo no pocos ejemplos.

Espero haber aclarado los principios comunes que trabajan bajo sistemas aparentemente tan diferentes y suscitar un interesante ejercicio personal o para vuestros estudiantes (lo siento, chavales… ¡deberes!).

Sobre el autor: Javier Fernández Panadero es físico y profesor de secundaria además de escritor de libros de divulgación.