Este pensador observó que todos los libros, por diversos que sean, constan de elementos iguales: el espacio, el punto, la coma, las veintidós letras del alfabeto. También alegó un hecho que todos los viajeros han confirmado: No hay en la vasta Biblioteca, dos libros idénticos. De esas premisas incontrovertibles dedujo que la Biblioteca es total y que sus anaqueles registran todas las posibles combinaciones de los veintitantos símbolos ortográficos (número, aunque vastísimo, no infinito) o sea todo lo que es dable expresar: en todos los idiomas. Todo: la historia minuciosa del porvenir, las autobiografías de los arcángeles, el catálogo fiel de la Biblioteca, miles y miles de catálogos falsos, la demostración de la falacia de esos catálogos, la demostración de la falacia del catálogo verdadero, el evangelio gnóstico de Basilides, el comentario de ese evangelio, el comentario del comentario de ese evangelio, la relación verídica de tu muerte, la versión de cada libro a todas las lenguas, las interpolaciones de cada libro en todos los libros, el tratado que Beda pudo escribir (y no escribió) sobre la mitología de los sajones, los libros perdidos de Tácito.

Jorge Luis Borges. La biblioteca de Babel.

A veces, muchos compositores eligen basarse en un mismo tema para escribir su música. Pero otras veces, las melodías de canciones diferentes se parecen sospechosamente entre sí sin que la atribución esté del todo clara. Es muy posible que, en estos casos, un compositor se inspirase en material ajeno, de forma consciente o inconsciente. Pero, ¿podría darse un “plagio” por pura casualidad? ¿Cuántas melodías distintas contiene la Biblioteca del Conservatorio de Babel?

A priori, podría parecer un problema relativamente sencillo. A fin de cuentas, la escala en la que se basa la música tonal occidental tiene sólo 7 notas (de do a si). Por pura combinatoria, se podría estimar que existen 7ⁿ melodías de n sonidos. Además, n no debería ser un número demasiado alto: a fin de cuentas, como ya hemos visto, la música tiende a basarse en motivos repetitivos que luego se desarrollan siguiendo distintos tipos de patrones. Si quisiésemos caracterizar La Folía, por ejemplo, n (el número de notas que dan identidad a su melodía) sería igual a 5. Pero se trata de un ejemplo quizás un poco extremo. Tomemos una melodía un poco más típica, como esta por ejemplo, y digamos que n=7. El resultado, a pesar de todas las simplificaciones asumidas, serían casi un millón de melodías.

7⁷ = 823.543 melodías de 7 sonidos y 7 notas

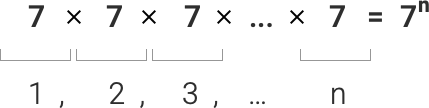
Pero… por supuesto, el problema no es tan sencillo. En realidad, nuestra identificación de una melodía nunca se basa en las notas exactas que la conforman (las frecuencias absolutas, por así decirlo) sino en la relación entre esas notas (la distancia entre esas frecuencias). Así, por ejemplo, si tomásemos todas las melodías formadas por las notas do y re (combinaciones de de dos símbolos en n posiciones distintas), encontraríamos que esas mismas melodías, solo que desplazadas hacia el agudo, pueden formarse con las notas re y mi, fa y sol, sol y la, la y si. Si queremos obtener una estimación más correcta, debemos buscar todas las simetrías posibles y eliminar sus repeticiones.

En ese sentido, la escala de 7 notas contiene bastantes simetrías: bastantes combinaciones de notas que son idénticas desde el punto de vista de las distancias (intervalos) que las separan. Para eliminarlas todas, es necesario identificar todos los grupos que se pueden formar con 1, 2, 3, 4, 5, 6 y 7 notas, considerando que la escala musical se repite de forma cíclica (después del si, “otra vez ya viene el do, oh, oh, oh”). De hecho, para resolver el problema por esta vía, debemos considerar que todos los dos, todos los res, todos los mis, etc. suenan iguales entre sí (son el mismo símbolo) independientemente de la escala a la que pertenezcan, cosa que no es del todo cierta… pero las gallinas esféricas se inventaron para situaciones como esta.

El número de melodías de n sonidos se calcularía entonces sumando todas las melodías diferentes que se pueden formar con 1 nota, con 2 notas, con 3 notas…, multiplicadas por el número de grupos distinguibles (desde el punto de vista de los intervalos) de 1 nota, 2 notas, 3 notas… hasta llegar a 7. El primer factor puede hallarse, nuevamente, por combinatoria y la única complicación es que cada combinación debe incluir todas las notas del grupo elegido (si no, sería igual a alguna combinación de un grupo de menos notas con otras simetrías características). Encontrar todos los grupos de notas diferentes entre sí es bastante más complejo, pero podéis ver algunas de las simetrías que existen en una escala en las siguientes figuras:

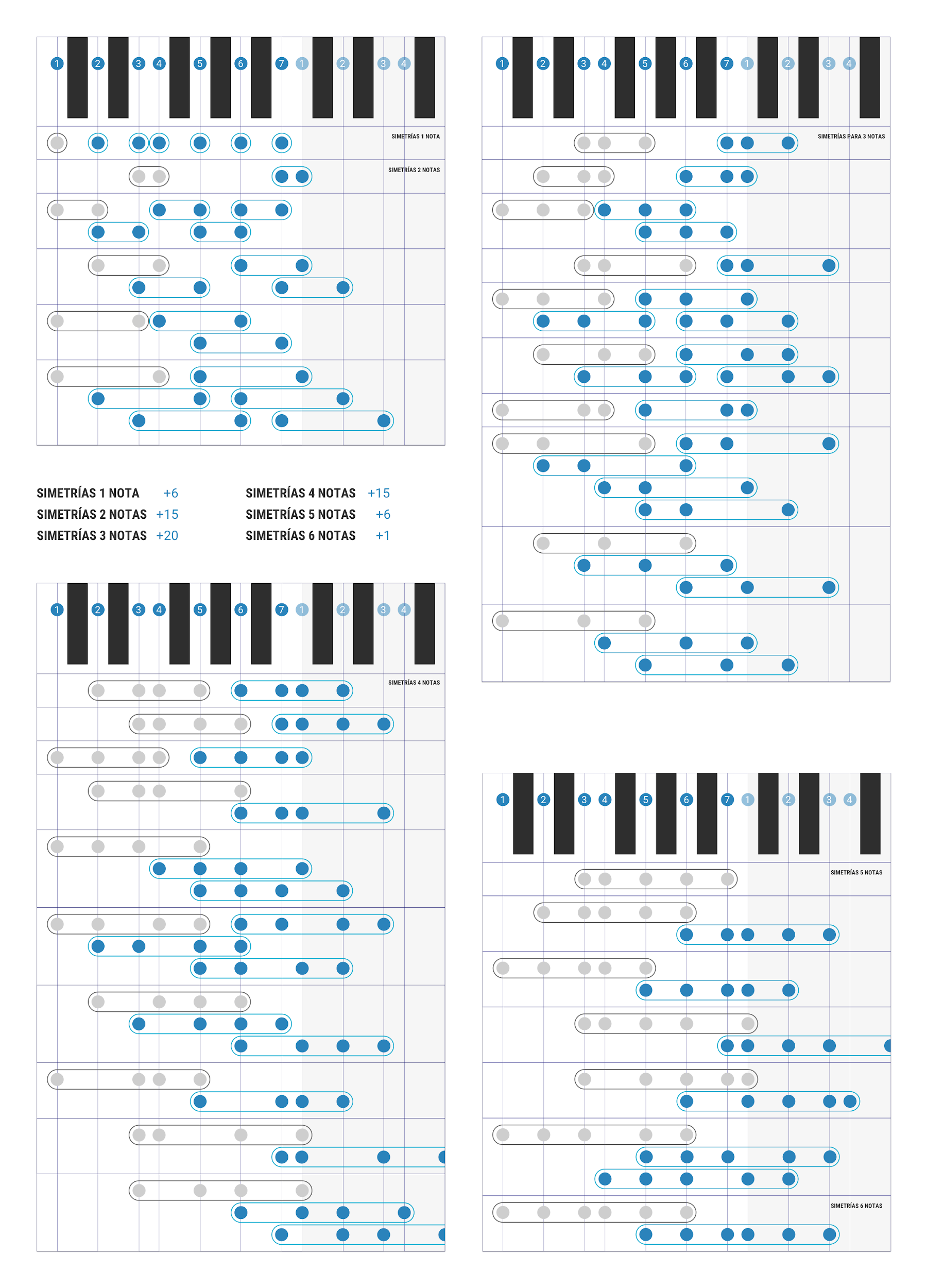
No quisiera abrumar a nadie con fórmulas y binomios de Newton, así que voy al grano. Así, además, igual alguien se pica y obtiene el mismo resultado. Según mis cálculos, con 7 notas pueden obtenerse:

543.544 melodías distintas de 7 sonidos y 7 notas

Pero… por supuesto, el problema no es tan sencillo. Está el tema de las escalas que comentábamos antes: realmente no todos los dos, todos los res, todos los mis etc. suenan igual. Pero sobre todo está el, quizás más importante, tema del ritmo. Sólo usando estas dos variables, Ligeti fue capaz de componer esta pieza con un extraño sentido del humor y sorpresa final. Quizás pueda resultar un tanto… repetitiva. Pero de eso va esta serie, después de todo.

De hecho, el ritmo, la duración relativa de los sonidos que componen una melodía, puede ser más importante para reconocerla que las notas en sí. Si no, no existiría la música para lápiz:

Da igual que el lápiz no esté “afinando” precisamente las notas. Basta la sugerencia del ritmo de una melodía conocida para identificarla de inmediato. Y basta el ritmo desnudo para crear música, prescindiendo por completo de cualquier melodía (pensad en una batucada, por ejemplo).

La buena noticia es que el ritmo es relativamente fácil de incluir en nuestro juego de combinatoria. Podemos, simplemente, multiplicar cada nota por tantas figuras rítmicas como queramos considerar. Supongamos que elegimos 3 figuras: corcheas, negras y blancas. Cada melodía de n sonidos posible se convertirá en 3ⁿ melodías y nuestro resultado crecerá hasta más de un billón:

1.188.730.728 melodías distintas de 7 sonidos y 7 notas de 3 duraciones distintas.

Pero… por supuesto, el problema no es tan sencillo. Porque la música no son sólo las notas de su melodía, ni siquiera el ritmo. De otro modo, no habría covers, ni versiones, ni homenajes; todas las folías serían la misma folía. La música es también, y sobre todo, timbre. Y el timbre ya no es codificable mediante un número tan acotado de símbolos…

Se trata, sin embargo, de una de las primeras propiedades sonoras que aprendemos a diferenciar de niños y, quizás, la que más nos guía a la hora de clasificar distintos estilos musicales: los instrumentos, la textura, la densidad sonora… todo lo que no es estrictamente melodía o ritmo. Existe un lugar común que critica la música popular contemporánea por ser (eso dicen) “toda igual”. Ciertamente, algunas canciones pop repiten esquemas armónicos y formales bastante sencillos, en comparación con, pongamos, los de la música de Wagner. Pero es que la innovación y la enorme riqueza de la música popular contemporánea procede, sobre todo, de su timbre. La gran revolución musical del s. XX no vino de mano de Cage ni de Boulez: consistió en añadirle un enchufe a todo lo que suena. De ahí, a las virguerías que hoy hace posible el mundo de la producción hay solo un paso.

¿Cómo podríamos incluir, entonces, esta nueva variable?, ¿cuántas melodías diferentes de 7 sonidos y 7 notas de 3 duraciones y diferentes timbres existen? Michael Stevens propone utilizar la codificación binaria de un CD para estimarlo y el resultado es… mayor que el número de átomos de hidrógeno que hay en el universo: 2^211000000, una cifra, simplemente, inimaginable.

Como en la Biblioteca de Babel, esos archivos de audio contendrían todas las posibles melodías escritas y por escribir, con toda su riqueza rítmica, melódica y tímbrica. También como en Babel, la mayoría de estos audios serían, simplemente, ruido. Pero, incluso si nos restringimos a la versión con notas y figuras acotadas: la mayoría de las melodías que obtendríamos por pura combinatoria carecerían de “sentido”. Del mismo modo que una cadena aleatoria de letras no forma necesariamente una palabra, cualquier combinación de notas no resulta “melódica”. Son nuestras propias expectativas, es nuestro propio conocimiento del lenguaje de la música lo que marca la diferencia. El mundo de las secuencias de sonidos posibles quizás sea inabarcable. Pero la librería de las buenas melodías debe escribirse, necesariamente, de una en una.

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica