En la anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica, Y tú, ¿cómo cuentas con los dedos? (1), inicié una pequeña serie de entradas sobre la cuestión de contar con los dedos de las manos. En dicha entrada abordé el tema de cómo contamos las personas, en la actualidad, con los dedos, y hoy vamos a continuar analizando esta cuestión.

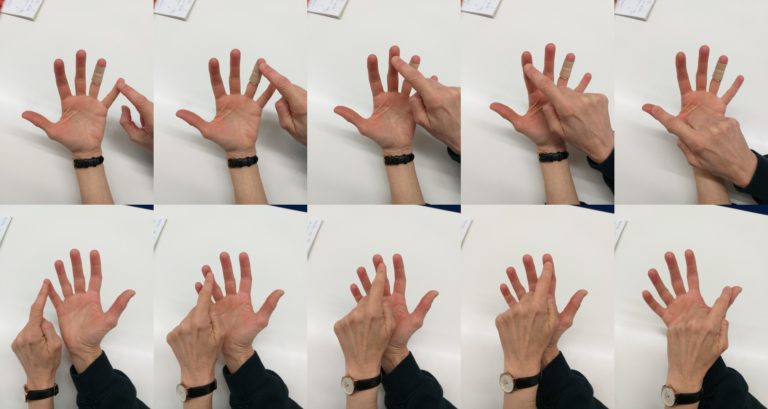
En la primera parte de esa primera entrada de la serie, realicé una pequeña encuesta a personas de mi entorno laboral, en la Universidad del País Vasco / Euskal Herriko Unibertsitatea, y de mi entorno de amistades. Descubrí que esencialmente contábamos de dos formas distintas. La técnica más habitual era partiendo de las manos cerradas y desplegando los dedos de las manos en un orden natural, con las variantes de empezar por la mano derecha o izquierda, y también empezando con el meñique o el pulgar, como hacía yo mismo, que era lo más habitual (véase la siguiente imagen).

La otra forma de contar más usual entre las personas entrevistadas era tocando en orden los dedos de cada mano con otro dedo, que podía ser el índice de la otra mano o el pulgar de la misma mano. Entre las personas entrevistadas que se tocaban los dedos con el dedo índice de la otra mano, las diestras solían empezar con el índice derecho tocando los dedos de la mano izquierda, aunque con la variante de empezar por el meñique o el pulgar, y luego cambiaban las manos, es decir, con el índice izquierdo tocaban los dedos de la mano derecha, como en la siguiente imagen. Y los zurdos al revés.
Para la segunda parte de esa primera entrada Y tú, ¿cómo cuentas con los dedos? (1) salí a la calle y empecé a preguntar a personas de mi barrio (vivo en el barrio bilbaíno de Bilbao La Vieja, donde viven personas de todas las partes del mundo) cómo contaban ellas con los dedos de las manos. A pesar de que vivimos en un mundo cada vez más global, donde se van uniformando las manifestaciones culturales, aún podemos apreciar las diferencias que existen entre las formas de contar en las diferentes partes del mundo, en las diferentes culturas.
Descubrí como algunas personas de diferentes países del mundo empiezan a contar con las manos abiertas y cerrando los dedos de cada mano. Entre ellas dos hombres de Nigeria, que empezaron por el dedo pulgar hacia el índice de la mano derecha, para contar del 1 al 5, y luego la izquierda, del 6 al 10. O un joven de Senegal, que utilizaba la misma técnica, pero empezando por la mano izquierda y el dedo meñique.
Pero esta forma de contar no es exclusiva de África. Para escribir esta segunda parte de la serie Y tú, ¿cómo cuentas con los dedos? he seguido preguntando a personas de otros países, entre ellas, algunas investigadoras e investigadores del Basque Center for Applied Mathematics (BCAM), es decir, el centro de investigación en matemática aplicada creado por el Gobierno Vasco en 2008, que está en Bilbao.
Entre las personas que entrevisté dentro de BCAM estaba Oleksii Sliusarenko, de Ucrania, que cuenta contrayendo los dedos, meñique (1), anular (2), corazón (3), índice (4) y pulgar (5), de la mano izquierda y luego, mientras mantiene la mano izquierda cerrada, continúa contrayendo los dedos de la derecha, para contar del 6 al 10 (como se muestra en la imagen). Según he leído esta es la forma en la que cuentan los países eslavos del este, como Bielorrusia, Rusia, Estonia, Letonia, Lituania o Moldavia.
En el libro Number words and number symbols de Karl Menninger se cuenta una historia que aparece en la novela The wind cannot read (1946) del escritor británico Richard Mason (1919-1997), que fue publicada en España como El viento no sabe leer (1955), y que está inspirada en las experiencias personales del escritor en tiempos de guerra, en concreto, en 1944, en la India, mientras aprendía japonés.
Durante la segunda guerra mundial, en la India, una joven india tiene que presentar a una de sus amigas, Sabby, a un hombre inglés que ha ido a su casa y que lleva tiempo viviendo en la India. El problema está en que su amiga es japonesa y en aquel momento, durante la segunda guerra mundial, si esto se sabe su amiga será arrestada. No olvidemos que India y Gran Bretaña eran países Aliados, mientras que Japón era un país de las Potencias del Eje, es decir, era un país aliado de la Alemania nazi. Por este motivo, la joven india presenta a su amiga como una mujer china, Miss Wei. El hombre inglés no acaba de creerse que esa mujer sea china, por lo que, para sorpresa de las personas presentes, le pide que cuente con los dedos de las manos, que cuente hasta cinco. La mujer, sin saber si es una broma o si el hombre está loco, se pone a contar con los dedos de su mano, uno, dos, tres, cuatro y cinco. Al terminar el inglés exclama “¡Ahí lo tenéis! ¿Habéis visto eso? ¿Habéis visto como lo ha hecho? Ella ha empezado con su mano abierta y ha ido doblando sus dedos uno a uno. ¿Habéis visto alguna vez contar así a una persona china? ¡Nunca! Los chinos, cuentan como los británicos. Empiezan con el puño cerrado y van abriendo los dedos de uno en uno. ¡Ella es japonesa!”

El investigador del Basque Center for Applied Mathematics, Dae-Jin Lee, que dirige la línea de investigación de BCAM de Estadística Aplicada, y cuya familia es de Corea, me ha contado que él aprendió a contar de pequeño de la siguiente forma. Cuenta del 1 al 5 por el método de “contraer los dedos de la mano”. Empieza con la mano izquierda abierta y va doblando los dedos, primero el pulgar (1), índice (2), corazón (3), anular (4) y finalmente, el meñique (5). Con la mano en esta posición, cerrada, puede continuar contando, levantando los dedos, desde el meñique (6), hasta el pulgar (10), como muestra la siguiente imagen. Es decir, con una sola mano cuenta del 1 al 10.
Esta es también la forma en la que cuentan los japoneses, luego la forma en la que contaba la mujer japonesa, Sabby, de la novela de Richard Mason.

Dae-Jin me ha contado que la otra mano, la derecha, la utiliza, cuando es necesario, para las decenas. Para contar las decenas, curiosamente, él despliega los dedos de la mano derecha, empezando por el pulgar para una decena, y seguiría el índice para dos decenas, esto es, veinte, y así continuaría.
Este matemático de origen coreano me ha contado también que su madre usa otro sistema, el Chisanbop, creado en los años 1940 en Corea, que permite contar con las dos manos hasta 99 y realizar operaciones aritméticas básicas. Volveremos más adelante con este método.
Ahora, veamos ahora cómo cuentan las personas chinas, y veamos si tenía sentido la distinción de la novela de Richard Mason. Del uno al cinco se parece al método que parece que utilizan, o utilizaban mayoritariamente, los británicos. Al parecer, los británicos y norteamericanos, tienden a contar de la siguiente forma: despliegan los dedos, empezando por el índice (1), hasta el meñique (4) y luego el pulgar (5), de una mano, para después pasar a la otra. Este aparece en la película de Quentin Tarantino, Malditos bastardos (2009), en la que un espía británico que se hace pasar por oficial alemán es descubierto ya que al pedir tres cervezas en un bar lo hace mostrando al camarero los dedos índice, corazón y anular, al estilo británico y estadounidense, mientras que para los alemanes, al igual que los franceses, sería más normal que mostrasen el dedo pulgar, índice y anular.

Aquí tenéis la escena en el bar de la película Malditos bastardos, de Quentin Tarantino, que incluye el error en la forma de indicar tres cervezas y el posterior masacre en el bar:
Y la explicación del error en la misma película:
Seguramente eso sería lo normal en esos años, o incluso mucho antes, pero hoy en día pasará algo parecido a lo que mostramos en la primera entrega de esta serie, que hay una tendencia más marcada hacia un método, el que ha sido el predominante en esa zona geográfica, pero que también se dan otros métodos. Por una parte, vivimos en un mundo cada vez más global y con un contacto cada vez mayor entre culturas y, además, quizás el uso de los dedos para contar, aunque sigue siendo normal y habitual, no lo es tanto como hace años.
La forma de contar de Estados Unidos, la misma que la británica, la vemos también utilizada, de una forma un poco macabra, en el western de humor negro La balada de Buster Scruggs (2018), la última película de los hermanos Joel y Ethan Coen (gracias a “Masgël” por indicármelo, en los comentarios de la primera entrada de la serie):
El método de contar cerrando los dedos de cada mano, desde el pulgar al índice, como yo mismo hago y muchas de las personas de mi entorno, y que además hemos contado que es el método habitual de alemanes y franceses, me lo he encontrado en bastantes de los matemáticos y matemáticas entrevistadas en BCAM. Así cuentan también Argyrios Petras, de Grecia, Gabriela Capo (de soltera, Cirtala), de Rumanía, Marco Capo, de Venezuela, y Julia Kross, de Alemania.
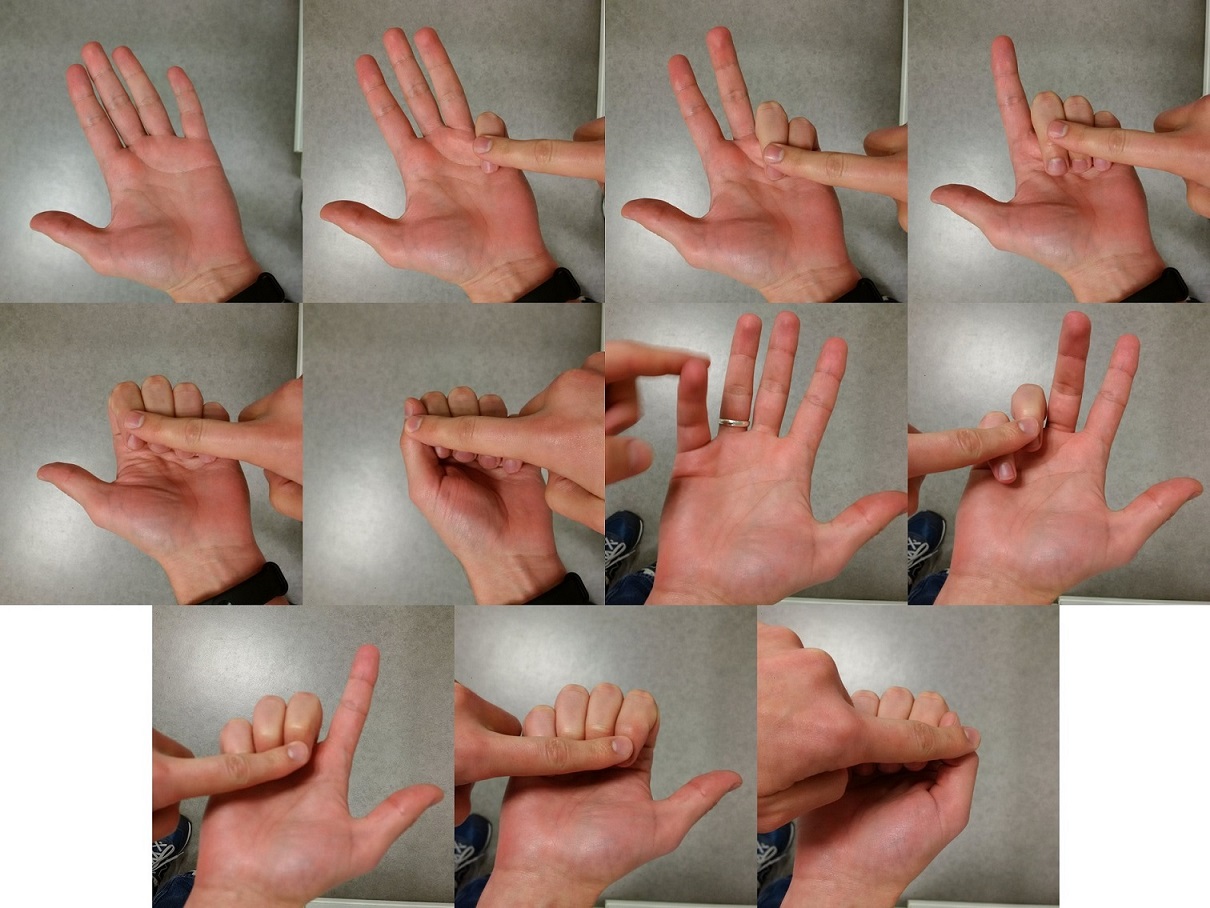
Pero volvamos al estilo de contar de las personas de china. Una de mis estudiantes de la asignatura de topología, en el grado de matemáticas de la Universidad del País Vasco, Xin Su, cuya familia es de origen chino, me ha explicado cómo cuenta ella, y su familia, del 1 al 10. La forma de contar de uno a cinco es bastante similar a la británica, como se decía en la novela El viento no sabe leer, se van desplegando los dedos, empezando por el índice, aunque para el número 3 cambian los dedos desplegados, en lugar de ser índice, corazón y anular, son meñique, anular y corazón, como se muestra en la siguiente imagen. El método para contar de seis a diez, que se sigue utilizando la misma mano, es más particular, trata de imitar los caracteres chinos para esos números, que vemos también más adelante.


Teniendo en cuenta que China es muy grande y con una gran diversidad cultural, nos podemos encontrar algunas variaciones al anterior método de contar con los dedos de las manos, en función de la parte de China en la que estemos. Por ejemplo, he visto como en algunos lugares representan el 10 realizando una cruz con los dedos índices de ambas manos o el 7 juntando todos los dedos.

Otra de las personas con las que me entrevisté en el centro de investigación en matemática aplicada del País Vasco fue el matemático Sandeep Kumar, de Rajastán, al noroeste de la India. Sandeep me habló de que utilizaba dos formas distintas de contar con los dedos. Una de ellas es la que hemos mencionado aquí como la técnica británica, es decir, se empieza con la mano cerrada, en su caso la izquierda, y se van abriendo los dedos en este orden, índice (1), corazón (2), anular (3), meñique (4) y pulgar (5), y de forma idéntica se continúa contando con la otra mano, del 6 al 10.
Sandeep me comentó que existía la posibilidad de empezar por el meñique, pero eso no era muy frecuente ya que en la India el gesto de levantar el dedo meñique significa que necesitas ir al baño, incluso de forma más específica, que vas a mear. La verdad es que este gesto llamó mi atención y decidí buscar cual podría ser el origen del mismo. Al parecer, según el hinduismo cinco son los elementos fundamentales para la creación del universo, los pancha mahabhuta, el fuego (agni), el aire (vayu), el éter (akasha), la tierra (prithvi) y el agua (apas o yala), los cuales se relacionaban antiguamente con los cinco dedos de la mano, en este orden, pulgar, índice, corazón, anular y meñique. De la relación del meñique con el agua podría venir el mencionado gesto.
El segundo método que utilizaba el matemático indio para contar era utilizando las falanges de las dos manos. En total tenemos 14 falanges en cada mano, dos en el pulgar y tres en el resto de dedos. Se empieza contando por la falange inferior del dedo meñique y se continúa contando, de abajo hacia arriba en cada dedo, del 1 al 14. Y con las dos manos se puede contar hasta 28.
En el libro Historia universal de las cifras, de Georges Ifrah, cuenta que un chino, de la provincia china de Cantón, le habló de un uso práctico de esa forma de contar que le había visto a su madre. Para contar los días del ciclo menstrual, que de media son 28, la madre anudaba un cordel en cada una de las 28 falanges, de las dos manos, según iban pasando los días del ciclo y así saber cuándo volvería a tener la menstruación (en ese tiempo no había aplicaciones móviles que te fueran avisando).
Aunque, como me contó Sandeep, hay quienes cuentan 14 en cada mano y quienes, como él, cuentan hasta 15, como si el dedo pulgar tuviese también tres falanges.

En el libro de Georges Ifrah, que cita el texto Les anciens prócedés de calcul sur les doigts en Orient et en Occident de J. G. Lemoine, relaciona esta forma de contar con el calendario hindú, que es lunisolar, es decir, tiene en cuenta tanto las fases de la luna, como del sol. Cada ciclo lunar se corresponde aproximadamente con 29,5 días, que da lugar al concepto de mes lunar (más o menos, 30 días, en realidad, 30 “días lunares”, tithi). Cada mes lunar contiene dos quincenas o fases de la luna (paksha), de unos 15 días. La primera es la fase de crecimiento, que va desde la luna nueva a la luna llena, llamada Shukla Paksha, y la segunda la de decrecimiento, que va desde la luna llena a la nueva, que recibe varios nombres, como Krishna Paksha. Los doce meses lunares se corresponden con aproximadamente 354 días, por lo que, más o menos, cada tres años se introduce un mes extra, que suele ser una repetición de unos de los meses normales, para ajustarlo al calendario solar.
Según menciona Georges Ifrah, esta forma de contar, que es la que utiliza el matemático indio Sandeep con quien estuve charlando sobre esta cuestión, se utiliza en la India, pero también en la península de Indochina (Camboya, Vietnam, Laos, Birmania y Tailandia) y la China meridional. Curiosamente, el calendario chino también es lunisolar.

Esta misma manera de contar la utilizaba otro de los matemáticos de BCAM, Mostafa Shahriari, de Isfahan, en Irán. Aunque el origen de ambas formas es distinto. Como ya expliqué en la entrada anterior Y tú, ¿cómo cuentas con los dedos? (1), en relación a la forma en la que contaba la familia de mi compañero Abdelmalik Moujahid, que es de Marruecos, esta técnica de conteo está relacionada con el Islam y los 99 nombres de Alá.

Mostafa también me explicó que en ocasiones también utilizaba otra forma de contar. Una de las comentadas en la anterior entrada. Tocando con el dedo pulgar el resto de los dedos, primero de la mano derecha, de meñique (1) a índice (4), y luego la mano extendida (5). Y con el mismo gesto en la otra mano del 6 al 10.
Este matemático iraní me explicó que en Irán no era normal contar como lo hacíamos muchos de nosotros, con el puño cerrado y levantando los dedos, empezando por el pulgar, porque el pulgar levantado solo era un gesto ofensivo, que significa lo mismo que, para nosotros, levantar el dedo corazón, lo que conoce como “sacar o enseñar el dedo” o “hacer una peineta”.
Según Georges Ifrah, el origen de la base 60 que utilizaron algunos pueblos antiguos como los sumerios o los babilonios es una mezcla de dos bases, la base 5, o incluso la decimal (10), y la base 12, que es una base muy versátil, por tener varios divisores, 2, 3, 4 y 6. Las bases 5 y 10 son muy naturales, ya que están relacionadas con nuestro cuerpo. Cada mano tiene cinco dedos y las dos manos tienen en total 10 dedos. Pero, ¿cuál es el origen de la base duodecimal?
La hipótesis que defiende Ifrah es que estaría relacionada con la manera de contar utilizando las falanges de las manos, ya que precisamente en la zona de Mesopotamia (Irán e Iraq, entre otros países) se sigue utilizando la técnica de contar las falanges. Según Ifrah, con el dedo pulgar se contarían las falanges de los otros cuatro dedos, a tres falanges por dedo, en total, doce falanges. La mano derecha se utilizaría para contar del 1 al 12, y la izquierda para los múltiplos de 12, luego en total, se podría contar hasta 144. Es decir, un sistema de numeración en base 12.

Vamos a terminar esta entrada explicando la manera de contar con los dedos de la madre del matemático de origen coreano del BCAM, Dae-Jin Lee, el chisanbop.
El chisanbop es un método para contar con los dedos inventado en Corea en la década de 1940. Sus inventores Sung Jin Pai y su hijo Hang Young Pai adaptaron la idea del ábaco coreano, que es un ábaco 1:4 igual que el soroban o ábaco japonés, a los dedos de la mano. La palabra chisanbop viene de las palabras coreanas chi “dedo” y sanpop “cálculo”.

Para el chisanbop cada una de las manos se corresponde con una de las varillas del ábaco coreano, la mano derecha para las unidades y la izquierda para las decenas, por lo que se pueden representar los números de una y dos cifras, es decir, del 0 hasta el 99.
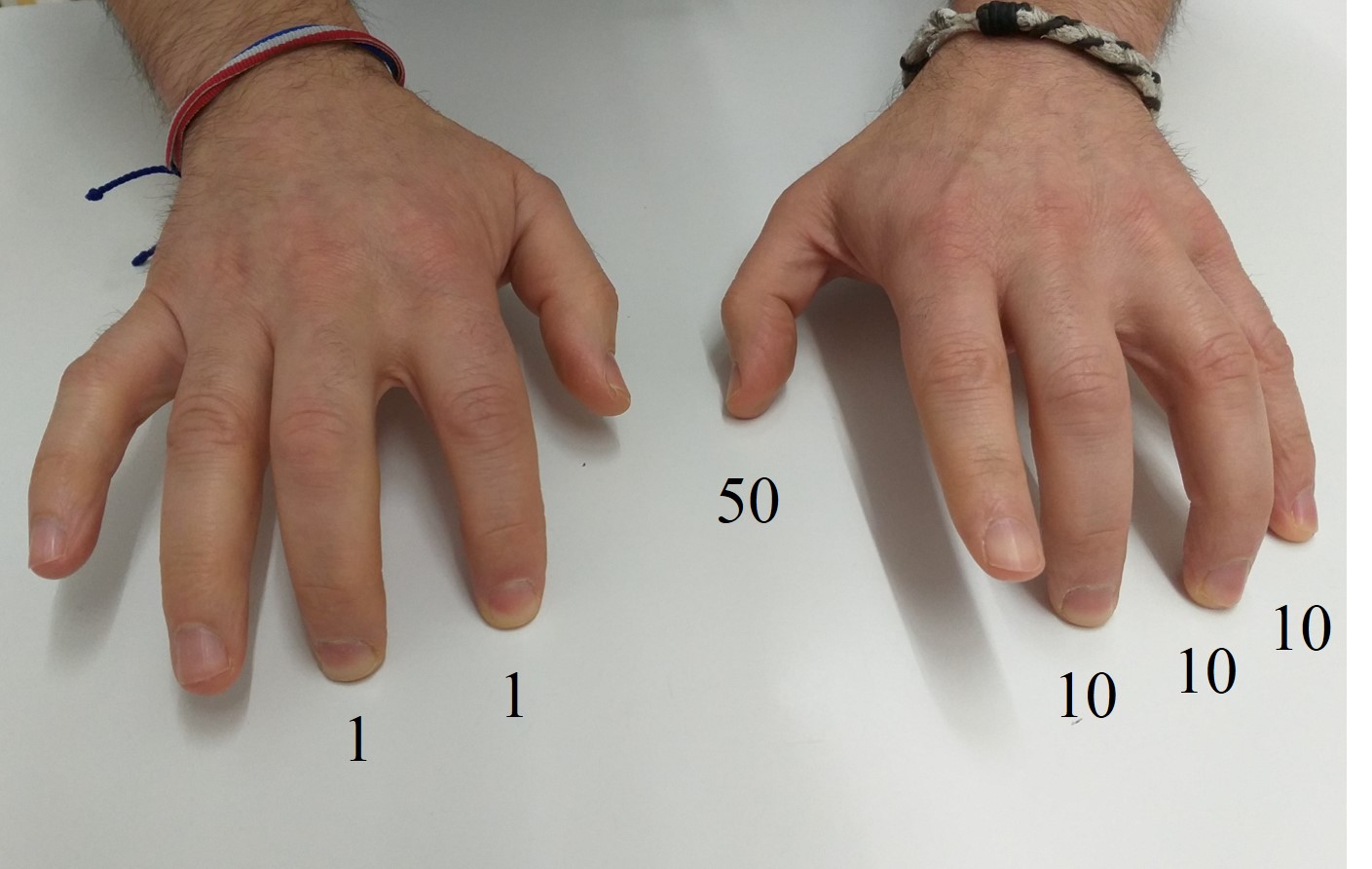
Los dedos índice, corazón, anular y meñique de la mano derecha toman en valor 1 (serían las 4 fichas de abajo en la varilla de las unidades en el ábaco), mientras que el pulgar toma el valor 5 (sería la ficha de arriba de la varilla de las unidades). Con esta mano, al igual que con la primera varilla del ábaco, podemos representar cualquier número de una cifra, del 0 al 9. Se empieza con la mano abierta, con la palma hacia abajo, en el aire o justo encima de una mesa y se bajan ligeramente, o tocando la mesa, los dedos que se quieren utilizar. Los dedos de las unidades se empiezan a usar en orden del índice al meñique. Así, para indicar el 1 se baja el índice, para el 2 el índice y el corazón, o para el 8 sería el pulgar, el índice, el corazón y el anular.

Los dedos índice, corazón, anular y meñique de la mano izquierda toman en valor 10 y el pulgar toma el valor 50, por lo que con esta mano se representan las decenas. Por lo tanto, con las dos manos se pueden representar todos los números de una o dos cifras, del 0 al 99. Así, en la siguiente imagen se está marcando el valor 82 con los dedos.
En la década de 1970 el chisanbop llegó a Estados Unidos y a raíz de su presencia en el Show de Johnny Carson llamó la atención del profesorado, la administración y los padres y madres, y se empezó a utilizar en algunos centros educativos.
Como punto final de esta entrada de la sección Matemoción del Cuaderno de Cultura Científica me gustaría agradecer la colaboración de todas las personas a las que he entrevistado tanto para la entrada anterior Y tú, ¿cómo cuentas con los dedos? (1) , como para esta. ¡Muchísimas gracias!

Bibliografía
1.- Levi Leonard Conant, Counting, The world of mathematics, volumen 1, James Newman (editor), Dover, 1956.
2.- Georges Ifrah, Historia universal de las cifras, Ensayo y pensamiento, Espasa, 2002 (quinta edición).
3.- Página web del artista Guido Daniele
4.- Página web del Basque Center for Applied Mathematics
5.- Karl Menninger, Number words and number symbols, Dover, 1969.
6.- J. G. Lemoine, Les anciens prócedés de calcul sur les doigts en Orient et en Occident, Revue des Études Islamiques 6, pp. 1 – 60, 1932.
7.- Página web del British Museum
8.- J. Dan Knifong, Grace M. Burton, Chisanbop: Just Another Kind of Finger Reckoning?, The Arithmetic Teacher 26, n. 7, pp. 14-17, 1979.
9.- Jay Greenwood, Critique on the Chisanbop Finger Calculation Method, The Arithmetic Teacher 26, n. 7, pp. 18-21, 1979.
10.- Página web del artista Einar Örn Benediktsson
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Marian
Hola,
Sólo quería hacer una pequeña aclaración a esta entrada que, como la serie, me está resultando divertida y fascinante a partes iguales.
Comentas que durante la Segunda Guerra Mundial, la India y Gran Bretaña eran «países aliados»; si mi memoria no me juega una pasada (lo cual no sería extraño), la India, por aquel entonces, seguía siendo una colonia británica, si bien es cierto que las revueltas en favor de la independencia habían comenzado décadas antes (desde finales del s. XIX).
La ley del parlamento británico en la que se reconoce la independencia de la India y Pakistán es de agosto de 1947 y el establecimiento de la República India tiene lugar en enero de 1950.
No quiero acabar este comentario sin agradecer las entradas que periódicamente realizas. Nunca dejan de sorprenderme. En más de una ocasión me he descubierto terminando de leerlas con una sonrisa en los labios. Por todo ello, GRACIAS.
Saludos cordiales,
Marian.
Raúl Ibáñez
Querida Marian,
Tienes toda la razón, por supuesto.
Muchísimas gracias por tus palabras. Me alegro de que te hayan gustado las dos entradas sobre contar con los dedos, y mis entradas en general. Me hace muy feliz saber que te has «descubierto terminando de leerlas con una sonrisa en los labios». Me parece uno de los cumplidos más bonitos que me han hecho. Muchas gracias.
Un fuerte abrazo, Raúl.
Masgüel
Y a veces, lo que diga el Partido:
https://www.youtube.com/watch?v=m6Ybkd_beUU
«Lo único que está en juego en el hecho de hacerle creer a Winston que dos más dos son cinco es el propósito de quebrantarlo. Hacer que una persona niegue una creencia sin que haya razones para ello constituye el primer paso hacia el objetivo de volverlo incapaz de tener un yo, porque se vuelve incapaz de urdir una trama coherente de creencia y deseo. La transforma en irracional, y ello en un un sentido preciso: no es capaz de dar, de su creencia, una razón que armonice con sus restantes creencias. Se convierte en irracional, no en el sentido de que pierda contacto con la realidad, sino en el sentido de que ya no puede dar explicaciones racionales: no puede ya justificarse ante si misma.»
Contingencia, ironía y solidaridad – R. Rorty
Masgüel
O lo que diga papá, que es profe de mates y también empieza por el índice.
https://www.youtube.com/watch?v=ZtUPKekDY7M
Raúl Ibáñez
Jajajajaja … que bueno 🙂
Raúl Ibáñez
Muchas gracias Masgël,
Vaya película, y vaya libro. Una referencia importante en mi adolescencia.
Un fuerte abrazo, Raúl
foousy
para la parte 3: http://www.intuitor.com/counting/
por cierto que si no conocéis el website, la sección Amazing Applications of Probability and Statistics es muy ilustrativa, y la Insultingly Stupid Movie Physics es ilustrativa, divertida y famosa.
salud!
Raúl Ibáñez
Muchísimas gracias,
Aunque ya está escrita la parte tres desde hace una semana :-). Y enviada. En ella explico la forma de contar binaria con los dedos de las manos y el sistema «romano» para contar hasta un millón…
En cualquier caso, muchisimas gracias por la referencia.
Un fuerte abrazo, Raúl.