Tenemos muy pocos doctores en matemáticas en Francia, aunque nuestros agregados tengan una gran cultura. Es porque los franceses huyen de lo mediocre y, temiendo no hacerlo más que pasablemente, muchos no hacen nada que podrían hacer muy bien. A pesar de sus brillantes cualidades, sin la guerra, el Sr. Antoine quizá nunca habría hecho un trabajo personal. Su ejemplo invita a atreverse.

Henri Lebesgue, informe sobre la tesis de Louis Antoine (traducida de la original en [6]).

A Louis Antoine (1888-1971) le citamos en el artículo Haciendo matemáticas en la oscuridad como uno de los matemáticos que realizaron grandes contribuciones a la ciencia a pesar de su ceguera.

Antoine comenzó sus estudios en la École normale supérieure en 1908, graduándose en 1912. El matemático Gaston Julia (1893-1978) ingresó en 1910 en aquella universidad y ambos se hicieron grandes amigos.

Antoine era subteniente en reserva en el 72 regimiento de infantería y, al declararse la Primera Guerra Mundial, fue movilizado. Desde el 2 de agosto de 1914 combatió como comandante de la segunda sección de ametralladoras del 151 regimiento de infantería. Fue herido por metralla el 25 de agosto y el 30 de octubre cuando se encontraba en una trinchera cerca de Ramscapell (Bélgica). Fue condecorado en varias ocasiones por su valentía.

Durante la ofensiva de Nivelle, el 16 de abril de 1917, su grupo atacó la plaza de Brimont. Fue herido por tercera y última vez: una bala le alcanzó la cara, perdió los dos ojos y el sentido del olfato. Su amigo Gaston Julia le acompañó durante su larga recuperación: compartían habitación en el sanatorio ya que una grave herida en la cara había hecho perder la nariz a Julia. El matemático Henri Lebesgue (1875-1941) les visitaba con frecuencia.

Antoine tuvo que dejar su trabajo como docente en enseñanza secundaria. A pesar de que recibía una pensión como inválido de guerra, deseaba retomar su actividad. Así que Louis Antoine comenzó a estudiar braille. Sus amigos Henri Lebesgue, Marcel Brillouin (1854-1948) y Gaston Julia hicieron copiar en braille los principales tratados matemáticos de la época. Las fórmulas matemáticas no tenían manera de transcribirse en este sistema de lectura, así que Antoine y un alumno de la École normale supérieure de Saint-Cloud, inventaron signos, aun utilizados en nuestros días, para los símbolos matemáticos.

Lebesgue sugirió a Antoine que se pasara a la enseñanza superior. Pero para ello debía defender una tesis doctoral. Como había poca bibliografía en Analysis Situs (topología) –y por lo tanto pocas publicaciones para traducir– Lebesgue le orientó hacia esa rama, proponiéndole extender al espacio tridimensional un resultado que se verificaba en el plano: el teorema de Jordan-Schönflies. Este teorema afirma que cualquier curva cerrada simple del plano lo divide en dos regiones, una acotada y otra no acotada, regiones que son además homeomorfas a las dos regiones delimitadas por la circunferencia unidad.

El 9 de julio de 1921, tras grandes esfuerzos, Antoine defendió su tesis de estado en Estrasburgo: Sur l’homéomorphie de deux figures et de leurs voisinages, memoria que contiene lo esencial de sus trabajos científicos. Antoine se dio cuenta de que el teorema de Jordan-Schönflies era falso en dimensión 3 –de hecho solo funciona en dimensión 2–, construyendo el denominado collar de Antoine, un conjunto homeomorfo al conjunto de Cantor y embebido en el espacio tridimensional.

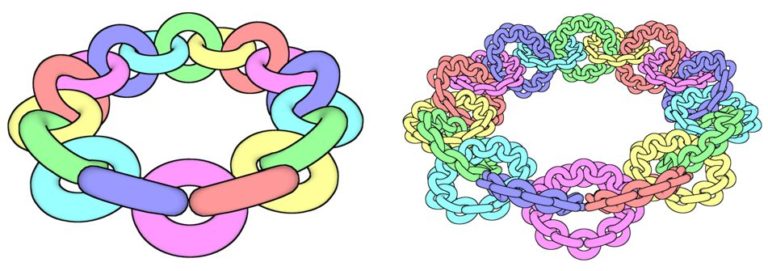
El collar de Antoine se construye de manera inductiva: se parte de un toro sólido –el producto de una circunferencia y un disco cerrado, es decir, una rosquilla– X₁. En el interior de X₁ se embeben cuatro toros sólidos enlazados, más pequeños, que forman los eslabones de una cadena: X₂ es la unión de estos cuatro toros. Dentro de cada toro sólido que forma X₂ se repite la misma operación, y así sucesivamente. En la etapa n-ésima, X_n estará formado por 4^n-1 toros enlazados, en cada uno de los cuales se embeben otros cuatro toros más pequeños aún, y la unión de los 4ⁿ toros enlazados definirá X_n+1.

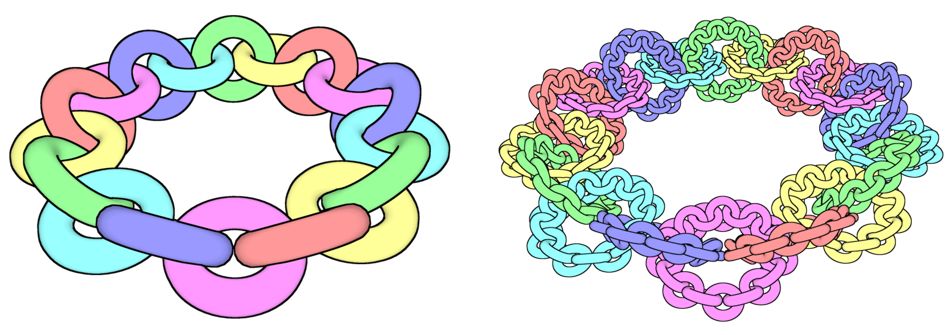
El collar de Antoine A es la intersección de esos X_n: A es un conjunto no vacío (por ser la intersección de conjuntos cerrados encajados), cerrado, totalmente disconexo (no tiene subconjuntos conexos con más de un punto), no posee puntos aislados y tiene el cardinal del continuo. Es decir, A es (homeomorfo a) el conjunto de Cantor. Además, R³–A no es simplemente conexo. Los detalles de la prueba pueden verse en [1] o en [3].

James W. Alexander (1888-1971) construyó en 1924 la denominada esfera de Antoine-Alexander –no es la misma que la esfera con cuernos de Alexander–, una esfera salvaje que contiene al collar de Antoine. se trata de un contraejemplo a la conjetura de Schoenflies en el espacio euclídeo de dimensión tres.

Probablemente Lebesgue tenía razón al afirmar que sin la guerra, Louis Antoine no habría construido ese bello y complejo ejemplo que lleva su nombre. Como comenta Gaston Julia en [5], esta frase resume el esfuerzo de Antoine en su lucha por seguir adelante:

El pensamiento es solo un destello en medio de una larga noche, pero este destello lo es todo.

Henri Poincaré

Referencias

[1] Louis Antoine, Sur l’homéomorphie de deux figures et de leurs voisinages, Thèse présentée à la Faculté des Sciences de Strasbourg, 1921

[2] Beverly L. Bechner and John C. Mayer, Antoine’s necklace or how to keep a necklace from falling apart, College Mathematics Journal 19 (4) (1988) 306-320

[3] H. Ibish, L’oeuvre mathématique de Louis Antoine et son influence, Expositiones Mathematicae 9 (3) 1991 251-274

[4] Allyn Jackson, The World of Blind Mathematicians, Notices of the AMS 49 (10) (2002) 1246-1251

[5] Gaston Julia, Notice nécrologique sur Louis Antoine, Comptes Rendus de l’Académie des Sciences de Paris 272 (1971) 71–74

[6] Jean Lefort, Louis Antoine, un mathématicien aveugle, Pour la Science 352, 2007

[7] Marta Macho Stadler, Louis Antoine y su fabuloso collar, ::ZTFNews, 2013

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.