Hemos visto que las ondas pueden pasar una a través de otra y sortear obstáculos en sus trayectorias. Las ondas también se reflejan, al menos en cierta medida, cada vez que llegan a cualquier límite del medio en el que viajan. Los ecos son ejemplos familiares de la reflexión de las ondas sonoras. Todas las ondas comparten la capacidad de reflejarse, algo que tiene muchos usos, como veremos en la próxima entrega. Nuevamente, el principio de superposición será el que nos ayude a comprender qué sucede cuando hay reflexión.

Supongamos que uno de los extremos de una cuerda está muy bien atado a un gancho firmemente sujeto a una pared [1]. Desde el otro extremo enviamos un pulso por la cuerda hacia el gancho. Como el gancho no puede moverse, la fuerza ejercida por la onda de la cuerda no puede hacer ningún trabajo en el gancho [2]. Por lo tanto, la energía transportada en la onda no puede abandonar la cuerda en este extremo fijo. ¿Qué hace la onda entonces? Rebota, se refleja, con la misma energía [3].

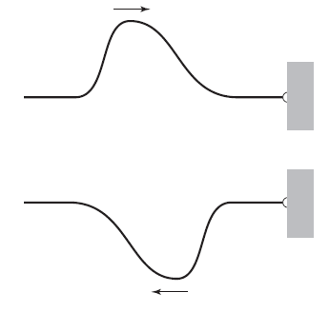
¿Qué aspecto tiene la onda después de reflejarse? El sorprendente resultado es que la onda parece ponerse del revés en la reflexión. Imaginemos que la onda viene de izquierda a derecha, como en la Figura 1, y se encuentra con el gancho fijo. El efecto de la onda es intentar levantar (subir) el gancho. Según la tercera ley de Newton, el gancho debe ejercer una fuerza sobre la cuerda en la dirección opuesta mientras se lleva a cabo la reflexión. Los detalles de cómo varía esta fuerza en el tiempo son algo complicados y no los trataremos aquí, pero el efecto neto es que se envía de vuelta por la cuerda una onda invertida de la misma forma.

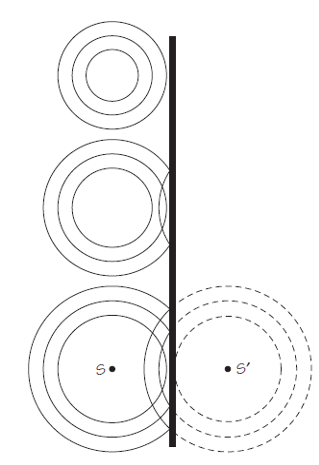
Fijémonos ahora en los tres diagramas de la Figura 2. Muestran los resultados de la reflexión de ondas en la superficie del agua en una pared recta. Puedes verificar si los diagramas son precisos al intentar reproducir el efecto en un lavabo o en una bañera. Espera hasta que el agua esté quieta, luego sumerge brevemente la punta del dedo o deja caer una gota en la masa de agua. En el diagrama de arriba, la cresta más exterior de la onda está cerca de la pared situada a la derecha. Los siguientes dos diagramas muestran las posiciones de las crestas después de que primero una y después dos se hayan reflejado.

Fijémonos en las curvas discontinuas en el último diagrama. Muestran que la onda reflejada parece originarse desde un punto S‘ que está tan lejos detrás de la pared como S está delante de ella. La fuente imaginaria en el punto S’ se llama imagen de la fuente S.

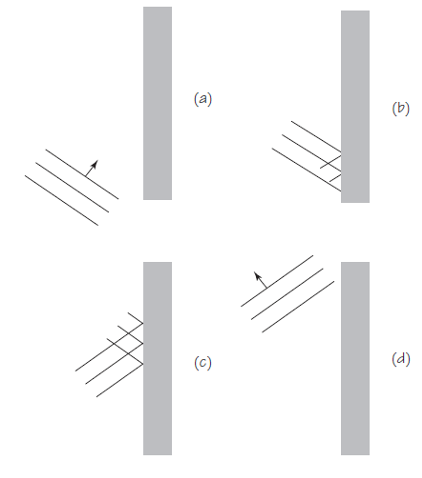
Hemos visto primero la reflexión de las ondas circulares, porque eso es lo que generalmente tenemos costumbre de ver cuando vemos ondas en la superficie del agua. Pero, en general, es más fácil usar un principio general para explicar la reflexión observando un frente de onda recto, reflejado desde una barrera también recta. Veamos los diagramas de la Figura 3 que indican lo que sucede cuando las crestas de las ondas se reflejan desde la barrera recta.

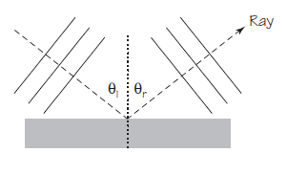
Parece que describir el comportamiento de los frentes de onda reflejados va a ser algo complicado. Sin embargo, es mucho más fácil si dibujamos perpendiculares a los frentes de onda. A esas líneas las vamos a llamar rayos, e indican la dirección de propagación de la onda. En la Figura 4 se han dibujado rayos para un conjunto de crestas onduladas justo antes de la reflexión y justo después de la reflexión desde una barrera. El rayo para las crestas incidentes forma un ángulo Θ_i con la pared. El rayo para las crestas reflejadas forma un ángulo Θ_r. El ángulo de reflexión Θr es igual al ángulo de incidencia Θ_i ; es decir, Θ_i = Θ_r.

Esto es un hecho experimental, que puedes verificar fácilmente.

Notas:

[1] Para ser rigurosos hemos de señalar que la pared tiene una masa enorme, está construida sólidamente y que no va a verse afectada en absoluto por lo que haga la cuerda.

[2] Que no puede hacer ningun trabajo significa que no puede desplazarlo (trabajo en física es fuerza por el desplazamiento que provoca), por estar anclado firmemente a una pared de las características de [1].

[3] Idealmente. Para que fuera exactamente así pared, gancho, sujeción al gancho y cuerda tendrían que ser ideales.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance