
Si una compañera y tú sacudís ambos extremos de una cuerda tensa con la misma frecuencia y la misma amplitud, observaréis un resultado interesante. ¡La interferencia de las ondas idénticas provenientes de extremos opuestos hace que ciertos puntos de la cuerda no se muevan en absoluto! Entre estos puntos nodales toda la cuerda oscila hacia arriba y hacia abajo. Pero no hay propagación aparente de los patrones de onda en ninguna dirección a lo largo de la cuerda. Este fenómeno se llama onda estacionaria. Pero démonos cuenta de una cosa: la oscilación estacionaria que se observa es realmente el resultado de dos ondas que sí se propagan.
Veámoslo primero empíricamente (fenomenológicamente, dirían los filósofos) para en la próxima anotación analizarlo con lo que ya sabemos de ondas.
Comencemos con el caso más simple. Para conseguir una onda estacionarias en una cuerda no es necesario que haya dos personas agitando los extremos opuestos. Un extremo se puede atar a un gancho en una pared o al picaporte de una puerta. El tren de ondas enviado por la sacudida del extremo libre de la cuerda se reflejará en el extremo fijo. Estas ondas reflejadas interfieren con las nuevas que se desplazan en el sentido opuesto, y es esta interferencia la que puede producir un patrón estacionario de nodos y oscilaciones.
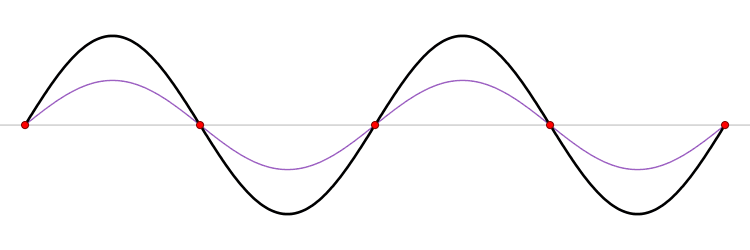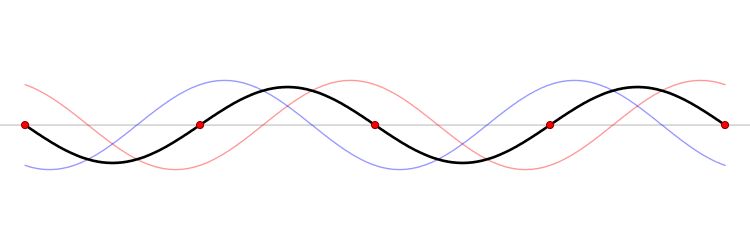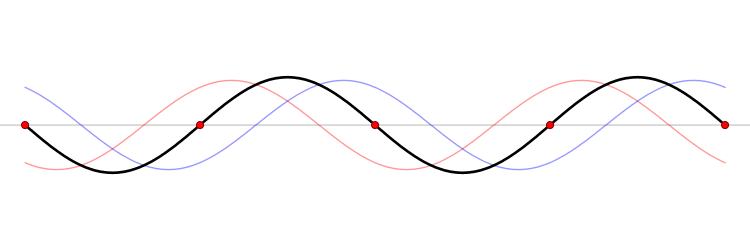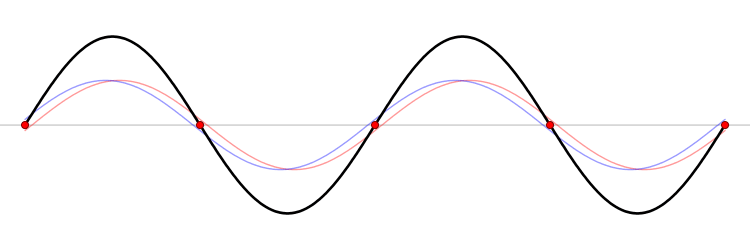
Pero no hace falta sacudir un extremo. De hecho podemos atar ambos extremos de la cuerda a puntos fijos y pulsar la cuerda, como la de un arco. Desde el punto pulsado, un par de ondas salen en direcciones opuestas y luego se reflejan en los extremos. La interferencia de estas ondas reflejadas que viajan en direcciones opuestas puede producir un patrón estacionario como antes. Las cuerdas de guitarras, violines, pianos y todos los demás instrumentos de cuerda actúan de esta manera. La energía dada a las cuerdas crea ondas estacionarias. Parte de la energía se transmite entonces desde la cuerda vibrante al cuerpo del instrumento; las ondas de sonido enviadas desde allí tienen esencialmente la misma frecuencia que las ondas estacionarias de la cuerda.
Las frecuencias de vibración a las que pueden existir las ondas estacionarias dependen de dos factores. Uno es la velocidad de propagación de la onda a lo largo de la cuerda. El otro es la longitud de una cuerda. La conexión entre la longitud de la cuerda y el tono musical que puede generar esta cuerda se ha conocido durante milenios y contribuyó indirectamente a la idea de que la naturaleza se basa en principios matemáticos.
Al comienzo del desarrollo de los instrumentos musicales, los músicos reconocieron y empezaron a saber producir ciertas armonías agradables al pulsar una cuerda cuya longitud se modificaba por la existencia de diferentes puntos fijos, ya fuesen cuerdas de una longitud dada atadas a extremos de madera como en una lira, ya una cuerda en la que se hacía una presión con los dedos de la mano que no pulsaba (o usaba un arco para inducir la vibración) a distintas longitudes premarcadas. Las armonías se producen si la cuerda es pulsada mientras está restringida a longitudes que corresponden a proporciones de números enteros pequeños. Así, la relación de longitud 2: 1 da la octava, la 3: 2 la quinta, y la 4: 3 la cuarta.
Esta sorprendente conexión entre armonía musical y números simples (enteros) animó a los pitagóricos a buscar otras relaciones numéricas o armonías en el Universo. Este ideal pitagórico influyó mucho a la ciencia griega, y muchos siglos más tarde inspiraron gran parte del trabajo de Kepler. En general, el ideal se mantiene vivo a día de hoy en muchas aplicaciones de las matemáticas a la experiencia física que son consideradas bellas, habiendo quien incluso establece la belleza como guía de descubrimiento.
En este vídeo puede verse un uso creativo de armonías usando ondas estacionarias en cuerdas dispuestas de diferente manera. En él aparece mi admirada Cynthia Miller Freivogel (solista) que usa un instrumento de ondas estacionarias para uso con arco (un violín barroco) construido por Schorn en Salzburgo en 1715, antes de que se supiese mucho sobre la física de las ondas.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Física de las ondas estacionarias: frecuencia fundamental y sobretonos — Cuaderno de Cultura Científica
[…] razón física de la aparición de notas armoniosas y la relación entre ellas no eran cosas conocidas por los griegos. Pero utilizando el principio de […]