El Centro Internacional de Cultura Contemporánea TABAKALERA, de Donostia/San Sebastián nos ha regalado estos días una maravillosa exposición de la artista donostiarra Esther Ferrer, comisariada por Laurence Rassel y Mar Villaespesa. Bajo el título Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… (del 5 de abril al 26 de mayo de 2019), la exposición recoge, en cuatro espacios conectados de Tabakalera, cuatro grupos de obras emblemáticas de la artista Esther Ferrer: proyectos espaciales, una visión general de las performances más significativas de su carrera (con realizaciones de las performances cada viernes), obras de la serie Poema de los números primos, y cuadros de la obra Pi.

Los números primos constituyen un elemento fundamental en la obra artística de Esther Ferrer, que ella ha utilizado desde las décadas de los años 1970 y 1980, a través de diferentes estructuras espaciales planas, como la conocida espiral de Ulam.

La propia artista, con motivo de su exposición en Artium en 2011, explica el origen de su trabajo con representaciones espaciales de los números primos:

“Tras algunos años, en la década de los 70, realizando proyectos con estructuras geométricas definidas únicamente en función de mis propios criterios, sentí la necesidad de pensar otras en las cuales mis preferencias estéticas jugaran un papel secundario. Estructuras libres que pudieran evolucionar por sí mismas, según su lógica interna…

Durante algún tiempo no conseguí un resultado que me satisficiera hasta que una noche soñé con los números primos, así empecé la serie, EL POEMA DE LOS NÚMEROS PRIMOS.”

Además, el título de la serie juega con la similitud de las palabras poema y teorema (recordemos que un teorema es una verdad matemática demostrable), “poema = teorema – ter + p”, así mismo este título nos habla de la poesía que está detrás de los números, en particular, de los números primos.

Pero vayamos con los objetos matemáticos utilizados por la artista donostiarra, los números primos, la espiral de Ulam y otras estructuras geométricas planas formadas por números.

Aunque seguramente todas las personas que estáis leyendo esta entrada del Cuaderno de Cultura Científica conocéis el concepto de número primo, siempre es conveniente empezar por el principio. Los números primos son aquellos números que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 25 no es un número primo ya que se puede dividir por 5, además de por 1 y 25, o tampoco el 33, divisible por 3 y 11, mientras que el número 17 sí es primo, ya que solamente es divisible por el 1 y el mismo, al igual que los números 2, 3, 5, 7, 11, 13 o 19.

El teorema fundamental de la aritmética, que ya aparece en el libro Los Elementos, de Euclides de Alejandría (aprox. 325 -265 a.n.e.), y que nos dice que todo número puede expresarse, de forma única, como producto de números primos, por ejemplo, el número 924 es igual al producto de 2 x 2 x 3 x 7 x 11, pone de manifiesto la importancia de esta familia de números. Además, este resultado es el motivo por el cual el número 1 no se considera un número primo, puesto que en ese caso no se daría la unicidad.

En la Antigua Grecia ya conocían también un método para obtener números primos, conocido como la criba de Eratóstenes. Este método aparece descrito en el texto Introducción a la Aritmética, del filósofo y matemático Nicómaco de Gerasa (aprox. 60 – 120 n.e.), quien atribuye su autoría al sabio polifacético griego Eratóstenes de Cirene (276-194 a.n.e.), aquel que también estimó de forma muy certera el diámetro de la esfera terrestre (véase El tamaño sí importa, que se lo pregunten a Colón (o de la geometría griega para medir el diámetro de la Tierra)).

El método de la criba de Eratóstenes consiste en lo siguiente. Consideremos todos los números naturales hasta uno dado, por ejemplo, tomemos uno bajo para ilustrar el concepto, el 25. En primer lugar, escribimos todos los números hasta ese número:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.

El 1 no es primo, luego lo tachamos, es decir, lo eliminamos como número primo. Después tenemos el 2, que sí es primo, lo marcamos (nosotros lo hemos puesto en negrita) y tachamos todos los múltiplos de 2, los números pares, que no serán números primos, puesto que los podemos dividir por 2.

El siguiente número que aparece es el 3, que es primo, lo marcamos y tachamos todos los múltiplos de 3, puesto que no son primos.

El siguiente número que aparece es el 5, que, puesto que no está tachado (esto nos expresa que no es divisible por ningún número anterior), es un número primo, luego lo marcamos y tachamos sus múltiplos, los que aún no estén tachados.

El siguiente número no tachado es el 7, luego es un número primo, y debemos de tachar sus múltiplos, así hasta recorrer toda la lista hasta el número final, en este caso el 25. En este sencillo caso nos quedaría:

Luego, los números primos menores que 25 son 2, 3, 5, 7, 11, 13, 17, 19 y 23.

Este es un método sencillo que nos permite ir obteniendo números primos hasta un número dado, aunque es un método con muchas limitaciones, ya que no permite conocer si un número en concreto, por ejemplo, el número 76.243, es primo o no, para saberlo la criba debe de llegar hasta ese número (en este caso, sí es primo), ni generar números primos, ni conocer sencillas propiedades de estos números, como, por ejemplo, si existen infinitos números primos.

Puesto que nuestros elementos de escritura, como una hoja de papel, son rectangulares, y además una línea continua de números se nos extendería mucho, lo normal es representar los números, hasta el número considerado, en un rectángulo de números, como el que aparece abajo y aplicar sobre el mismo el método de la criba de Eratóstenes.

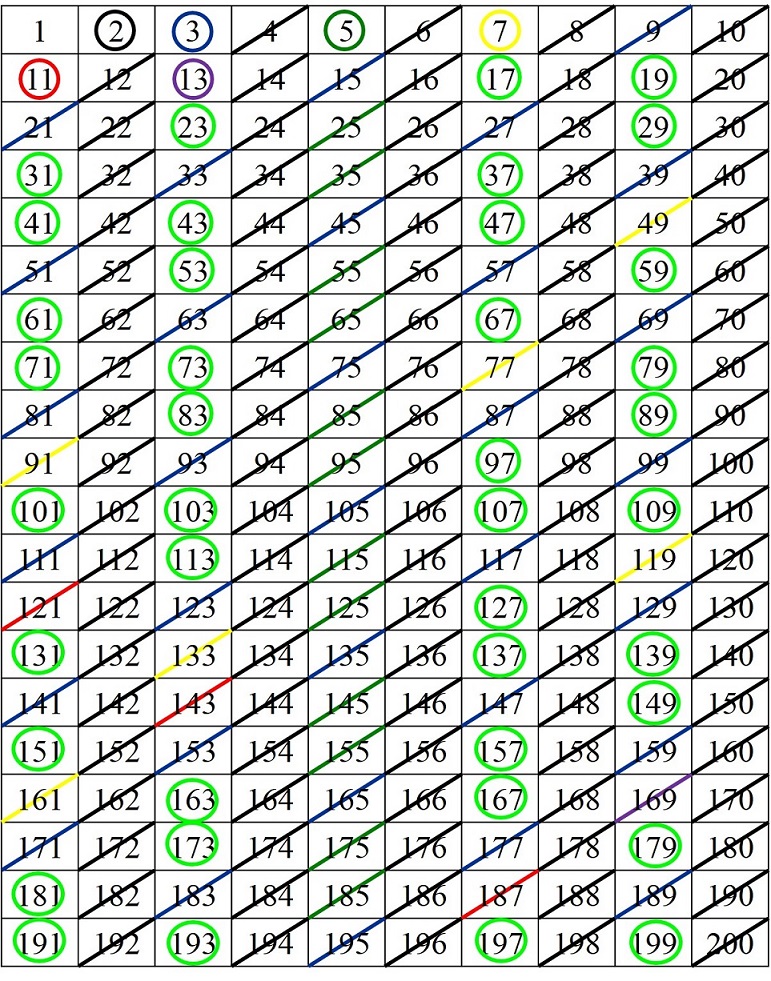
Así, los números primos hasta el 200 son:2, 3, 5, 7, 11, 13, 17, 19, 23, 29,31, 37, 41, 43, 47, 53, 59, 61, 67, 71,73, 79, 83, 89, 97, 101, 103, 107, 109, 113,127, 131, 137, 139, 149, 151, 157, 163, 167, 173,179, 181, 191, 193, 197, 199.

La criba de Eratóstenes, expresada de esta forma, ya es una estructura geométrica plana, rectangular, que nos puede permitir buscar información de la estructura de la familia de números primos, como patrones visuales que puedan producirse a partir de los cuales obtener dicha información. Por ejemplo, aunque esto es evidente sin necesidad de la criba de Eratóstenes, podemos observar que todos los primos están en cuatro columnas, que se corresponden a los números que terminan en 1, 3, 7 y 9. Y nos permite ver que hay muchas parejas de números primos gemelos, que son aquellos números primos que están lo más cerca posible, es decir, con tan solo un número par entre ellos, como las parejas 11 y 13, 17 y 19, 41 y 43, 59 y 61, 71 y 73, 101 y 103, 107 y 109, 137 y 139, 149 y 151, 179 y 181, 191 y 193, 197 y 199, que se corresponden con las terminaciones (1, 3), (7, 9) o (9, 1). Estas parejas de números primos gemelos también han interesado a la artista Esther Ferrer.

Antes de continuar con la espiral de Ulam, remarquemos dos hechos muy importantes relacionados con los números primos, que juegan un papel central en la serie Poema de los números primos de la artista donostiarra y de los que ya hablamos en la entrada del Cuaderno de Cultura Científica Buscando lagunas de números primos, que existen infinitos números primos y que cada vez existen menos números primos en la recta de los números naturales, es decir, la densidad de números primos según vamos avanzando en los números naturales es cada vez menor.

“Un día soñé que nadaba en un mar de números y después del sueño todos los que se me venían a la cabeza eran primos. Así fue como empecé a trabajar en la serie Poema de los números primos, y a plantearme la cuestión del infinito, que trabajé más tarde recurriendo a Pi, sin duda un número infinito.”

(Conversación entre Esther Ferrer, Laurence Rassel y Mar Villaespesa en Esther Ferrer, todas las variaciones son válidas, incluida esta, 2017)

La anterior obra tiene como base una criba de Eratóstenes rectangular de 76 columnas, es decir, la primera fila son los números del 1 al 76, y 99 columnas, luego nos determina los números primos hasta el número 7.524 (76 x 99). Esther Ferrer construye esta criba de Eratóstenes en la que se producen cuatro columnas vacías de números primos (la de la derecha, debajo del cero, es un añadido para dar simetría a la estructura), correspondientes a las columnas debajo del 19, 38, 57 y 76, múltiplos de 19.

Esther Ferrer genera, a través de su mirada personal, una determinada estructura espacial que subyace a la distribución real de los números primos dentro de la recta de los números naturales, que es una realidad del universo de los números, pero que observamos a través de la mirada creativa de la artista. Esta hermosa obra ha sido realizada en el suelo del Palacio de Velázquez, en el Parque del Retiro de Madrid, para la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta (2017). Además, al realizarla a un tamaño grande, dispuesta en el suelo y sobre la que pasear, cautiva a las personas que pasean sobre ella y realza aún más el impacto de la estructura de los números primos.

Martin Gardner en su artículo The remarkable lore of the prime numbers cuenta que el matemático polaco Stanislaw Ulam (1909 – 1984), quien participó en el proyecto Manhattan y desarrollo junto con el matemático húngaro John Von Newmann (1903 – 1957) el método de Montecarlo, estaba escuchando una conferencia en el Laboratorio Científico de Los Álamos, que el propio Ulam describió como “un artículo largo y muy aburrido”, y empezó a hacer garabatos en una hoja, en concreto, empezó a escribir los números en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, e hizo un círculo alrededor de los números primos. Entonces se dio cuenta de que los números primos se concentraban en líneas rectas, especialmente en diagonales, así mismo, había algunas diagonales, como las formadas solo por números pares, en las que no había ningún número primo.

En Los Álamos disponían del ordenador MANIAC II, que tenía guardados en su memoria los primeros 90 millones de números primos, por lo que junto a Myron L. Stein y Mark B. Wells programaron el ordenador para que realizara una espiral de números, con los números naturales desde el 1 hasta el 65.000, en la que se marcaran solamente los números primos. La imagen que obtuvieron (que hemos incluido más abajo y que aparece en el artículo de Ulam, Stein y Wells, A visual display of some properties of the distribution of primes, 1964) confirmaba lo que había visto Ulam, que los números primos aparecen alineados en rectas horizontales, verticales y, sobre todo, diagonales.

A esta estructura geométrica plana en la que los números naturales son escritos en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, destacando los números primos, es lo que se conoce como la espiral de Ulam (dos imágenes más abajo puede verse con más claridad).

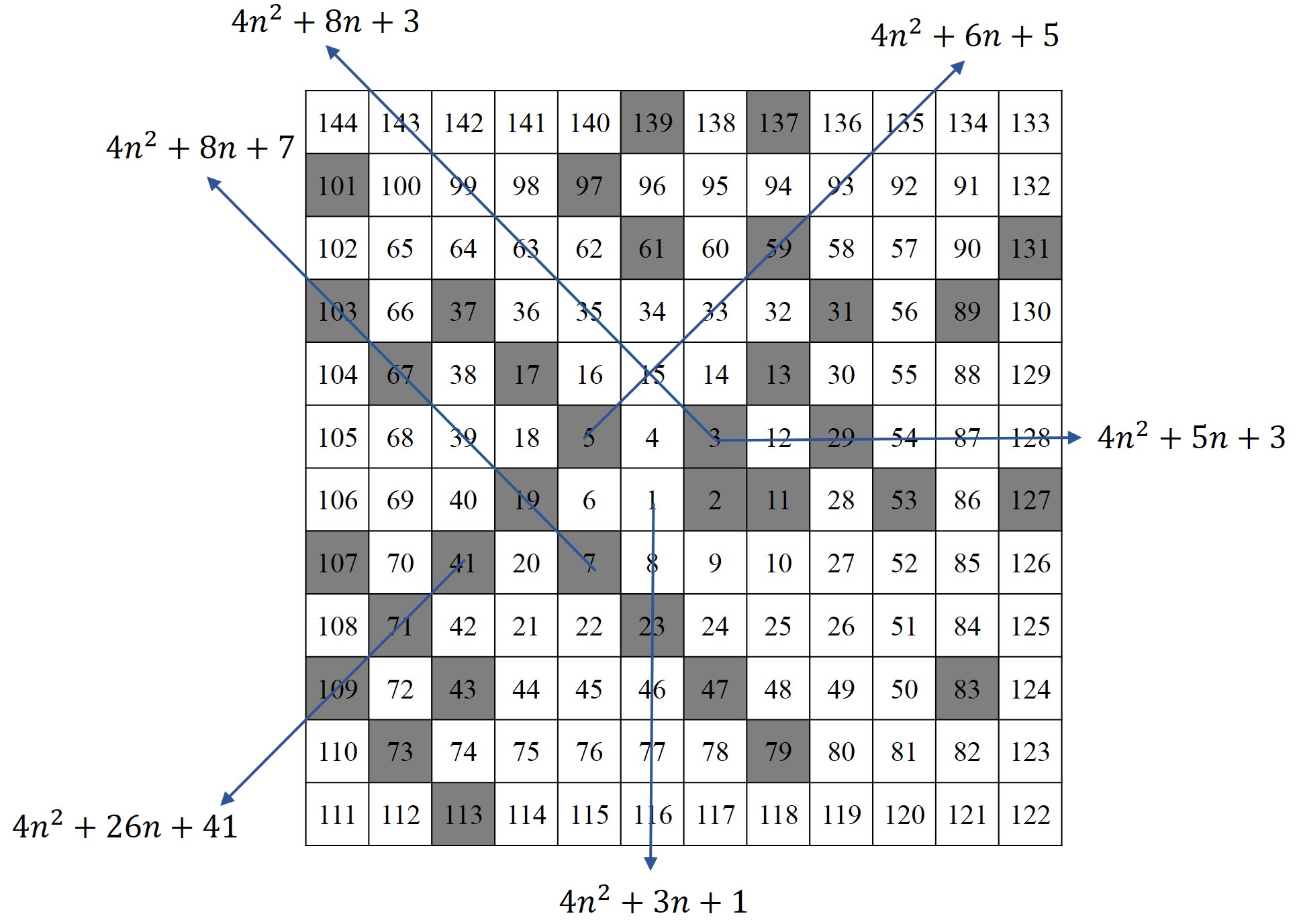
Detrás de esta observación de Stanislaw Ulam está el hecho de que los números de las líneas verticales, horizontales y diagonales se corresponden con los valores de los polinomios cuadráticos de la forma 4n² + bn + c, como puede verse en la siguiente imagen. En función de los valores de b y c se generan diferentes líneas que tendrán más o menos números primos. Por ejemplo, si b y c son pares, solo se producen números pares y no habrá números primos en dichas líneas, salvo quizás el 2. El polinomio de la imagen siguiente, 4n² + 8n + 3, es igual a (2n + 1)(2n + 3), luego no genera números primos, salvo el 3, para n = 0. Mientras que otras líneas, como la diagonal 4n² + 26n + 41, sí genera números primos, como 41, 71, 109 o 271, y no primos, como 155 y 209. Dos polinomios cuadráticos que generan muchos números primos son 4n² – 2n + 41, que a partir de un cierto valor de n genera la línea diagonal de puntos blancos en la parte de arriba de la imagen de Ulam, Stein y Wells (la imagen anterior), y 4n² + 2n + 41, que es la línea de abajo.

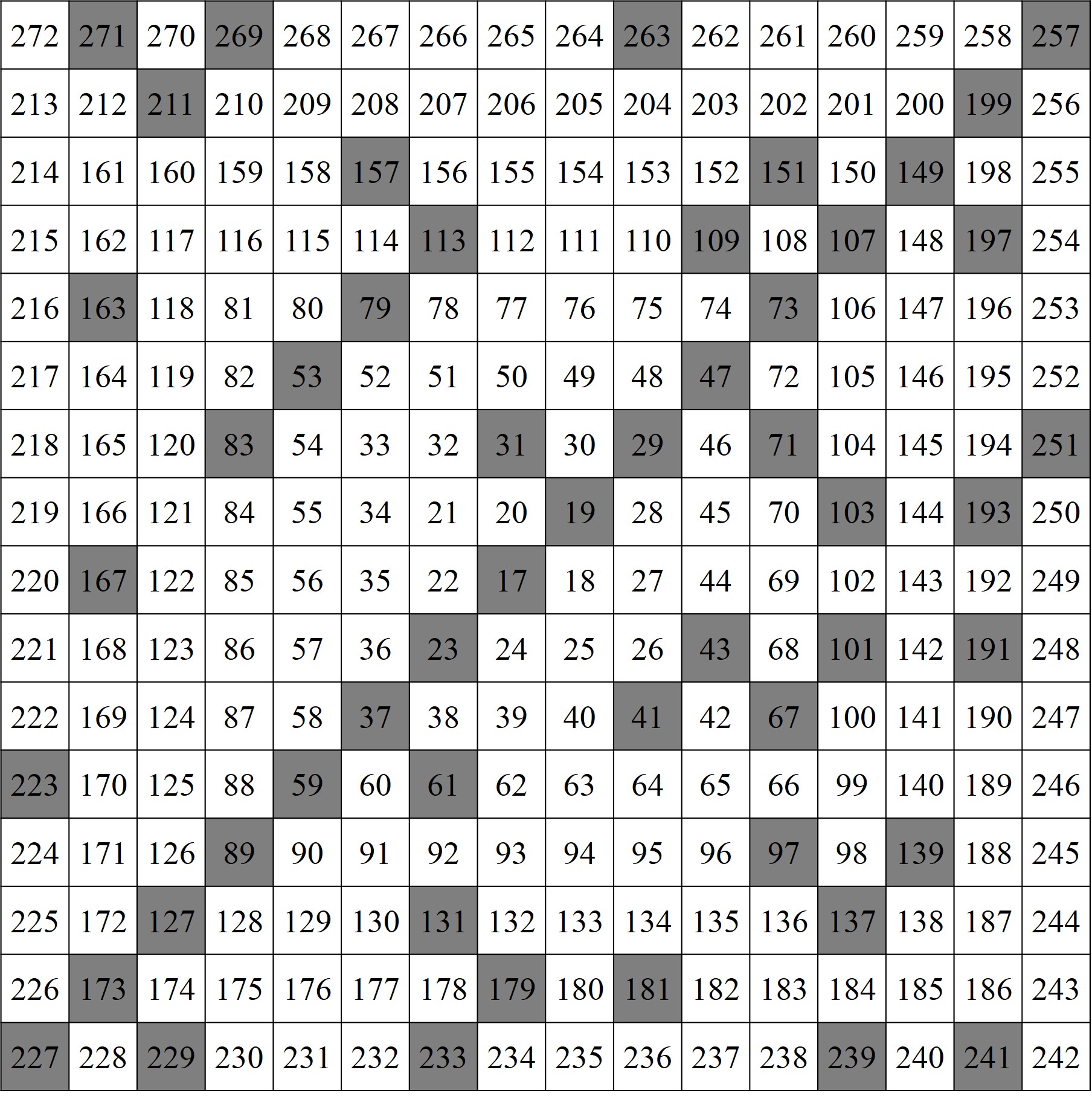
El siguiente dibujo de Esther Ferrer, de entre los años 1983 y 1985, nos da algunas claves de la forma en la que la artista trabaja con la espiral de Ulam. Para empezar el dibujo contiene la espiral de Ulam en una cuadrícula 16 x 16, luego con los números desde 1 hasta 256. Además, solo están escritos los números primos en la espiral y en las posiciones que corresponden a números compuestos, es decir, los números no primos, está dibujado un segmento diagonal “tachando” ese número, pero sin el número. En este dibujo, las diagonales tienen dos posiciones y dos colores posibles. El sentido de la diagonal y el color cambian cada vez que aparece un número primo, de forma que entre un primo y el siguiente, es decir, lo que conocemos como una laguna de números compuestos entre números primos (véase la entrada Buscando lagunas de números primos), las diagonales que aparecen tienen un mismo sentido y color. La confluencia de la construcción de la espiral de Ulam, junto con las diagonales inclinadas y de colores, confiere al conjunto de una estructura geométrica particular, casi laberíntica en este caso, que es el objetivo buscado por la artista.

Stanislaw Ulam también realizó una espiral similar, pero empezando con el número 17, de forma que los números de una de las dos diagonales principales se correspondían con los valores, desde n = 0 hasta 15, del polinomio n² + n + 17, eran números primos (17, 19, 23, 29, 37, …, 257), lo cual fallaba para el siguiente valor, n = 16, que es un número compuesto, 16² + 16 + 17 = 17². Este polinomio ya era conocido por el matemático suizo Leonhard Euler (1707 – 1783), como un polinomio que generaba muchos números primos.

Un polinomio que genera muchos números primos y que también era conocido por el matemático Leonhard Euler (1772) es n² + n + 41. Si se inicia la espiral de Ulam en el número 41, los números de la diagonal principal son valores de este polinomio generador de primos de Euler y para los valores entre n = 0 y n = 39, se genera un segmento continuo en esa diagonal de 40 números primos, que durante más de dos siglos fue el segmento más grande conocido de este tipo. Ulam, Stein y Wells encontraron que, para valores de n entre 0 y 10.000.000, el polinomio n² + n + 41 genera un 47,5% de números primos, casi uno de cada dos (aunque en esta entrada no vamos a dedicarnos a este tema, en matemáticas se han continuado estudiando polinomios que generan muchos números primos). Los valores de este polinomio n² + n + 41 son, en la espiral de Ulam empezando en 1, los valores del polinomio es 4m² + 170m + 1847, haciendo el cambio n = 2m + 42.

La espiral de Ulam empezando en el número 41 alcanzó cierta notoriedad por esa diagonal principal con un segmento de 40 primos seguidos, con el 41 en el medio, 19 primos hacia abajo en la diagonal, hasta el número 1523, y 20 primos hacia arriba, hasta el número 1601.

El anterior dibujo fue la base para la realización de una obra de la serie Poema de los números primos en el parque del Prado en Vitoria-Gasteiz, en 2003. Es una espiral de Ulam de 100 x 100 = 10.000 “números”, que empieza en el número 41 y cuyo último número primo es 10.039. Está realizada con baldosas de cerámica, de tamaño 20 x 20 cm cada una, en las que aparece una diagonal roja, una diagonal azul o un número primo. Luego el tamaño de la obra es de 20 x 20 metros.

Esther Ferrer explica así el objetivo de elegir esa obra para el parque del Prado de Vitoria-Gasteiz:

“– es una obra que incita a la reflexión puesto que no corresponde exactamente a los cánones más o menos establecidos sobre lo que es o no es una obra de arte,

– es una obra dinámica, con posibilidades de interactividad libre y espontánea, sin normas,

– además de su belleza intrínseca, esta pieza aporta un elemento lúdico, puesto que los niños que frecuenten el parque jugarán sobre ella y quizás inventarán a partir de la misma sus propios juegos,

– podrán también empezar a comprender que las matemáticas no son forzosamente aburridas, y que con ellas puede hacerse incluso arte,

– por último, podrán aprender, iniciarse, sin prácticamente darse cuenta, en el universo de los números primos, esos números tan particulares, casi mágicos, conocidos desde la más remota antigüedad y que actualmente presentan una gran utilidad en diferentes campos, tanto científicos, como técnicos.”

Como bien explica Esther Ferrer en su libro Maquetas y dibujos de instalaciones 1970/2011, para toda una serie de dibujos-maquetas de números primos, estos están “pensados para suelos, alfombras, murales por lo que pueden realizarse en materiales diversos (azulejo, lana, seda, hormigón,…). En los cuadrangulares o rectangulares se hace una cuadrícula y cada cuadrado es un número. Se marcan en esa enumeración los primos y luego se unen con hilos, o se dejan en blanco y el resto se colorea … según la variación elegida”.

En este dibujo podemos observar de nuevo, que uno de los elementos importantes en la reflexión artística de Esther Ferrer son las lagunas de números primos, es decir, las zonas de números compuestos, no primos, entre dos números primos. Así, en esta obra, la artista ha coloreado los cuadrados de los números compuestos de los colores negro o rojo en función de la laguna a la que pertenezca el número natural. Por ejemplo, entre los números primos 257 y 263 (abajo en la espiral) aparecen, en la espiral, cuadrados de color rojo correspondientes a los números compuestos entre ellos, 258, 259, 260, 261 y 262, mientras que los cuadrados de la siguiente laguna, entre los números primos 263 y 269, están pintados de negro, 264, 265, 266, 267, 268.

Según vamos avanzando en los números naturales hay una menor cantidad de números primos, una menor densidad dentro de los números naturales, y las lagunas entre números primos son cada vez mayores, como se puede observan en el siguiente dibujo, en el que la artista Esther Ferrer construye una espiral de Ulam empezando en el número 1.344.326.696.347. Como en el dibujo-maqueta anterior, se trata de una cuadrícula 21 x 21, es decir, la correspondiente espiral en ambos casos está formada por 441 números, aunque en este segundo caso hay muchos menos números primos y las lagunas de números primos (los números compuestos entre dos números primos consecutivos) son mayores.

A continuación, he repintado la estructura de la espiral de Ulam del anterior dibujo-maqueta, en colores azul y verde, para recuperar la espiral que subyace debajo de la obra, y para observar mejor las lagunas de números primos que existen.

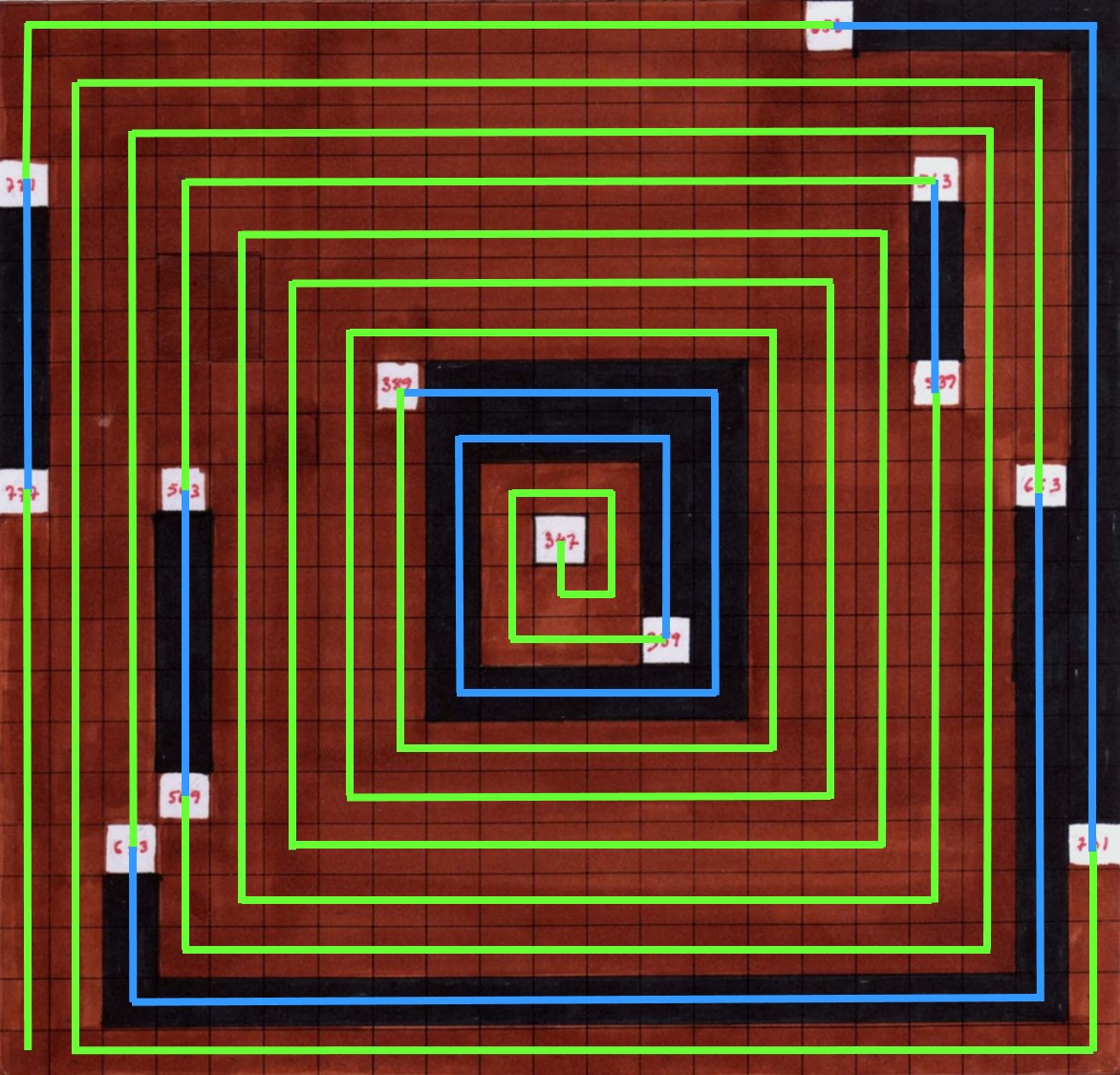
Dialogando con Laurence Rassel y Mar Villaespesa en Esther Ferrer, todas las variaciones son válidas, incluida esta (2017), la artista explica así su trabajo con la espiral de Ulam:

“… puedo trabajar los números primos a partir de la espiral de Ulam. Al utilizarla se crea una línea ininterrumpida durante cierta cantidad de números. Me gustó la idea de escribirlos en espiral, como una galaxia, los números primos tienen algo que ver con la estructura del universo; a medida que progresas en la serie hay menos números, el espacio entre ellos se agranda, me gusta ese vacío, es como si la serie se expandiera, como el universo.”

Existe toda una serie de obras de Esther Ferrer, pertenecientes a la serie Poema de los números primos, que tienen como punto de partida la espiral de Ulam, empezando en el número 41. A continuación, mostramos algunos ejemplos, que además nos muestran como la intervención creativa de la artista da lugar a diferentes resultados. La primera está realizada con hilos, alfileres de colores y tinta sobre lienzo, en la cual los colores están asociados con los números primos, de hecho, con la terminación en 1 (rojo), 3 (verde), 7 (azul) o 9 (amarillo) del número primo.

Las diferentes intervenciones artísticas de Esther Ferrer, sobre la misma base de la espiral de Ulam, generan diferentes patrones geométricos planos, como se pone de manifiesto con estas obras.

En la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… de Tabakalera también nos encontramos obras que surgen del mismo punto que las anteriores, la espiral de Ulam empezando en el número 41, pero, una vez más, con sus propias características fruto de la acción de la artista.

Y terminemos esta entrada, con unas palabras de la creadora donostiarra, con motivo de su exposición en Artium en 2011, en relación a su trabajo con los números primos:

“Lo primero que sorprende cuando se comienza a trabajar con la serie de los números primos es que – cualquiera que sea el sistema utilizado – el resultado es siempre equilibrado, hermoso, y lo segundo es que cuanto más grande es la obra, es decir, cuantos más números la forman, más interesante es la estructura, nunca simétrica, siempre en movimiento, por ello siempre he pensado en realizar obras monumentales como suelos, muros, tapicerías etc.

Al penetrar el universo de los números primos se tiene la sensación de que son la traducción, el reflejo, de un caos universal, magnífico, continuamente en evolución, que no se repite jamás, pero que, pese a ello, es siempre el mismo. Un caos en cuyo interior parece existir un orden, un orden extraño, curioso.”

Para concluir esta entrada, me gustaría expresar mi más sincero y profundo agradecimiento a Esther Ferrer por permitirme utilizar las imágenes de sus hermosas e interesantes obras en esta publicación, así como por las interesantes conversaciones que hemos mantenido sobre las matemáticas, y en particular, los números primos, en el conjunto de su obra artística.

Bibliografía

1.- Esther Ferrer, Maquetas y dibujos de instalaciones 1970/2011, Exit publicaciones, 2011.

2.- Rosa Olivares (comisaria), Esther Ferrer, Lau mugimenduan/En cuatro movimientos/In four movements, ARTIUM 08/10/2011 – 08/01/2012, Artium y Acción cultural española, 2011.

3.- Laurence Rassel y Mar Villaespesa (comisarias), Esther Ferrer, todas las variaciones son válidas, incluida esta, Palacio de Velázquez del Parque del Retiro 26/07/2017 – 25/02/2018, Museo Nacional Centro de Arte Reina Sofía, 2017.

4.- Martin Gardner, The remarkable lore of the prime numbers, Scientific American 210, n.3, 120 – 129, 1964.

5.- M. L. Stein, S. M. Ulam, M. B. Wells, A Visual Display of Some Properties of the Distribution of Primes, American Mathematical Monthly 71, p. 516 – 520, 1964.

6.- Paul Hoffman, El hombre que sólo amaba los números, la historia der Paul Erdös y la búsqueda de la verdad matemática, Granica, 2000.

7.- Wikipedia: Ulam spiral

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica