Hace casi dos años hablamos en este Cuaderno de Cultura Científica del teorema de Marion (Walter), un bonito enunciado de geometría afín, nombrado en honor a la matemática Marion Walter –que justamente ayer cumplió 91 años–.

Hoy traemos un objeto matemático, el grafo de Marion. En este caso, la matemática que da nombre a este grafo es otra Marion, Marion Gray.

Marion Gray nació en Escocia en 1902. Se interesó fundamentalmente por las matemáticas y la física. Estudió en la Universidad de Edimburgo y, tras graduarse, trabajó durante dos años como estudiante de postgrado bajo la supervisión del conocido matemático Edmund Taylor Whittaker.

En 1924 viajó a los Estados Unidos para estudiar en el Bryn Mawr College (Pensilvania). Allí aprendió matemáticas con Anna Johnson Pell Wheeler, David Vernon Widder y Marguerite Lehr. Defendió su tesis doctoral –The theory of singular ordinary differential equations of the second order– en 1926 bajo la supervisión de Anna Johnson Pell Wheeler.

Regresó a Edimburgo, donde trabajó como profesora asistente durante un año. De allí se trasladó a Londres donde trabajó como profesora asistente de matemáticas en el Imperial College durante tres años.

En 1930 regresó a los Estados Unidos y fue contratada como ingeniera asistente en el Departamento de Desarrollo e Investigación de la American Telephone and Telegraph Company de Nueva York.

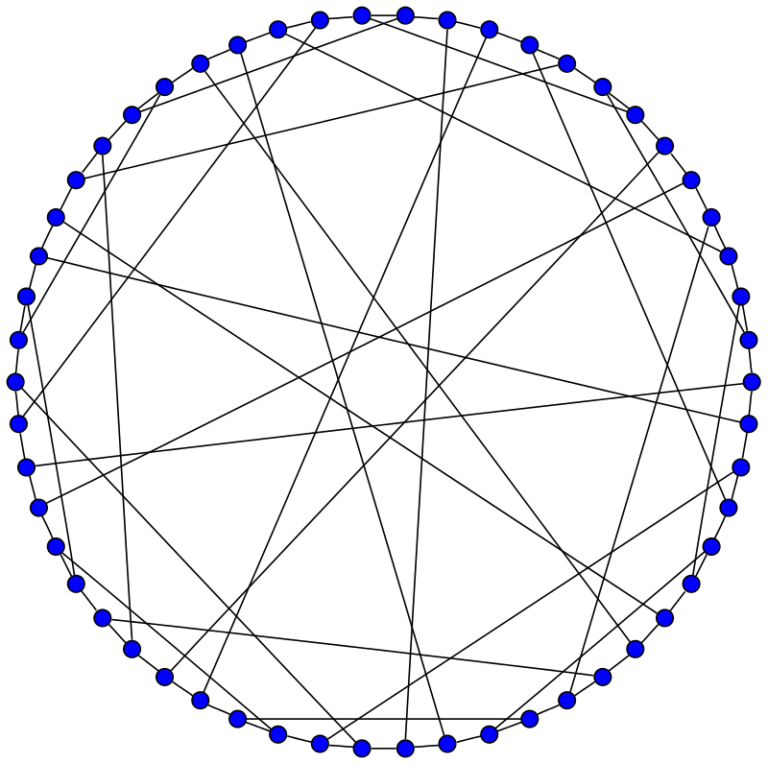
En 1932, buscando “redes completamente simétricas”, descubrió el grafo que lleva su nombre, un grafo cúbico con 54 vértices y 81 aristas.

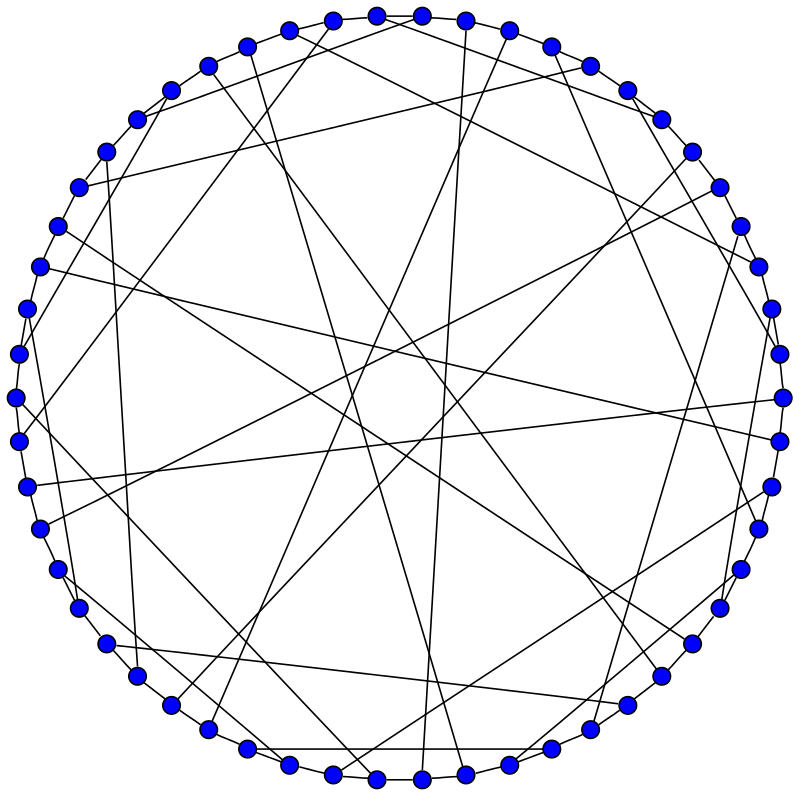
Aunque Marion no publicó nada sobre este grafo –pensaba que se trataba de un resultado teórico sin aplicaciones–, el matemático Izak Zurk Bouwer lo citó en su artículo An edge but not vertex transitive cubic graph [Canad. Math. Bull.11 (1968) 533-535], en el que lo describía –fundamentalmente sus propiedades de simetría– y comentaba en una nota a pie de página:

El grafo descrito en esta nota fue descubierto por la Dra. Marion C. Gray en 1932. El autor lo ha redescubierto de manera independiente y cree que aquí aparece publicado por primera vez.

En junio de 1969, Bouwer escribió a Gray para comentarle su aprecio por el hecho de que, en un momento en que la teoría de grafos era prácticamente inexistente, ella ya había encontrado este grafo con unas propiedades tan interesantes.

¿Y cuáles son esas propiedades tan interesantes? Además de las comentadas antes, el diámetro del grafo de Gray –la distancia maximal entre dos vértices– es 6, y la longitud de su ciclo más corto es 8. Es un grafo conexo, y para desconectarlo, es preciso eliminar como mínimo tres vértices o tres aristas.

Este grafo de Gray es además semi-simétrico –fue Bouwer quien lo probó en su artículo de 1968–, es decir, es arista-transitivo –existe un automorfismo del grafo que lleva cualquier arista en otra–, regular –todos los vértices tienen el mismo grado–, y no es vértice-transitivo –no existe ningún automorfismo del grafo que lleve cualquier vértice en otro–.

Además es el menor grafo cúbico semi-simétrico, como demostraron Aleksander Malnič, Dragan Marušič, Primož Potočnika y ChangqunWang en 2002 [An infinite family of cubic edge- but not vertex-transitive graphs, Discr. Math. 280, 133-148].

Por cierto, Marion se equivocó: este grafo –y otros similares– es fundamental en teoría de redes.

¿Y qué fue de nuestra protagonista? En 1934, se unió al personal técnico de los Bell Telephone Laboratories, donde pasó más trabajando de 30 años hasta su jubilación. Durante ese tiempo publicó varios artículos de investigación y realizó cientos de revisiones de trabajos de otros. También formó parte del comité que preparó el famoso Handbook of Mathematical Functions editado por Milton Abramowitz e Irene Stegun (1964).

Después de su jubilación, en 1967, Gray regresó a Edimburgo, donde falleció en 1979.

Referencias

• Marion Cameron Gray, MacTutor History of Mathematics, University of St. Andrews

• Judy Green and Jeanne Laduke, Supplementary material for pioneering women in American Mathematics: the pre-1940 Phd’s, pp. 218-220, AMS, 2009

• Catherine Booth, Celebrating Scottish women of science: Marion Gray (1902–1979), Discover NLS 23 (2013) 20–21

• Marta Macho Stadler, El grafo de Gray, de Marion Gray, ZTFNews, 16 septiembre 2014

• Gray Graph, Wolfram MathWorld

• Marion Cameron Gray, Wikipedia (consultado el 28 julio 2019)

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.