Una transformación biyectiva de una imagen de n por m píxeles es una modificación de esta figura en la que cada píxel se desplaza del lugar que ocupa a otro, y el que llenaba ese sitio se mueve a otra parte de esa imagen. De este modo ningún píxel desaparece, sólo cambia de posición. En matemáticas se dice que se ha realizado una permutación de los píxeles que componen la imagen.
Las transformaciones biyectivas de imágenes poseen la siguiente propiedad general:
Existe un menor número entero, k, de manera que realizando k veces la transformación se vuelve a obtener la imagen original.
Este resultado es una consecuencia inmediata del hecho de que el conjunto P de las permutaciones sobre un conjunto finito forma un grupo –el grupo simétrico, que en este caso, además, es un grupo finito–. Puede demostrarse que si P es una permutación de este tipo, existe un número entero k tal que si P se aplica k veces se recupera la transformación identidad –la permutación que no cambia nada–.
Para aclarar esta idea, supongamos un conjunto con cinco objetos {A,B,C,D,E} y llamemos P a la permutación que intercambia el primer y tercer objetos, lleva el segundo objeto a la cuarta posición, el cuarto al quinto lugar y el quinto pasa a ocupar la segunda posición. Puede simbolizarse esta transformación del modo ABCDE → CEABD. Si aplicamos sucesivamente P obtenemos las ordenaciones siguientes:
ABCDE → CEABD → ADCEB → CBADE → AECBD → CDAEB → ABCDE,
es decir, en seis iteraciones hemos regresado a la configuración inicial.
Por cierto, en este Cuaderno de Cultura Científica hablamos hace unos años de la transformación del fotomatón, que es un ejemplo de transformación biyectiva de una imagen.
La transformación (discreta) de la panaderai es un caso particular de transformación biyectiva de imágenes. La introdujeron en 1997 los matemáticos Jean-Paul Delahaye y Philippe Mathieu (ver [1] y [2]).
Su nombre se refiere al tipo de distorsiones que definen la permutación, que recuerdan al proceso de preparar una masa de pan, estirando y plegando la mezcla. En efecto, partimos de una imagen con un número par de filas n y columnas m. Los puntos –píxeles– de la primera línea tienen por coordenadas (de izquierda a derecha) (0,0), (1,0), (2,0), …, (m-2,0) y (m-1,0); las de la segunda línea (0,1), (1,1), (2,1), …, (m-2,1) y (m-1,1), etc. Y se procede del siguiente modo
- Estirado de “la masa”: mezclando líneas pares e impares
La altura del rectángulo de partida se divide por 2 y su longitud se multiplica por 2. Tras esta transformación, la primera línea pasa a ser (0,0), (0,1), (1,0), (1,1), …, (m-2,0), (m-2,1), (m-1,0) y (m-1,1), la segunda (0,2), (0,3), (1,2), (1,3), …, (m-2,2), (m-2,3), (m-1,2) y (m-1,3), y así sucesivamente.
-
Plegado de “la masa”: cortando el rectángulo obtenido en la etapa anterior en dos y colocando la parte derecha sobre la izquierda tras haberla hecho girar 180 grados.
Con esta segunda permutación, la primera línea se transforma en (0,0), (0,1), (1,0), (1,1), …, (m/2-1,0) y (m/2-1,1) y la segunda queda (0,2), (0,3), (1,2), (1,3), …, (m/2-1,2) y (m/2-1,3). Y los puntos de las últimas líneas que resultan del plegado de la mitad derecha quedan: (m-1,3), (m-1,2), (m-2,3), (m-2,2), …, (m/2,3) (penúltima línea) y (m/2,2), y (m-1,1), (m-1,0), (m-2,1), (m-2,0), …, (m/2,1) y (m/2,0) (última línea).
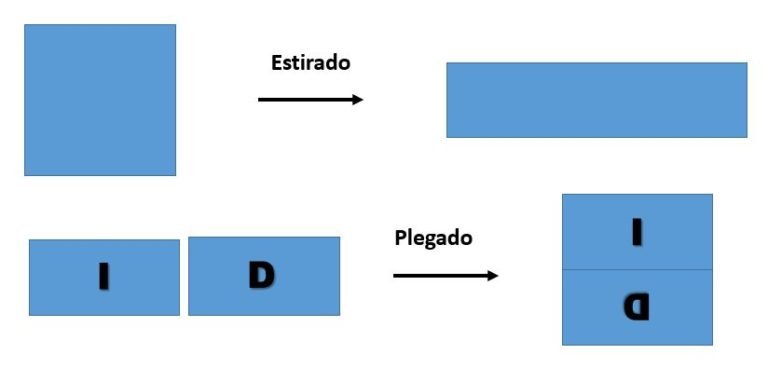
Observar que, tras realizar estas dos operaciones, se obtiene una imagen cuyas dimensiones coinciden con las de la imagen original. Es decir, es una imagen que posee n filas y m columnas, como la de partida. La transformación de la panadera es la obtenida tras realizar las operaciones de estirado y plegado.
Como la transformación (discreta) de la panadera es una permutación de n por m píxeles, si se aplica de manera iterada, llegará un momento en el que se debe recuperar la imagen original, tal y como se ha comentado antes.
Por ejemplo, si se toma una imagen de la Gioconda de n=256 por m=256 píxeles y se aplica la transformación de la panadera, se obtiene una figura como la que se muestra debajo:

Si se sigue aplicando sucesivamente la transformación de la panadera a cada imagen obtenida, tras 17 iteraciones, ¡la imagen original aparece! En este enlace podéis ver el proceso completo de cambio.
En la página de Philippe Mathieu se pueden ver otras transformaciones de imágenes mediante la transformación de la panadera y otras transformaciones biyectivas de imágenes.
Referencias
[1] Jean-Paul Delahaye y Philippe Mathieu, Images brouillées, Images retrouvées, Pour la Science 242 (1997) 102-106
[2] Jean-Paul Delahaye y Philippe Mathieu, Les transformations bijectives d’images, página web de P. Mathieu
[3] Marta Macho Stadler, La transformación del panadero, Boletín de la Titulación de Matemáticas de la UAL, vol. VIII, no. 1 (2014) 16-17
i Se suele llamar ‘del panadero’, pero la panadería de mi barrio está regentada por una mujer…
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
Pablo Rodríguez
Recuerdo un caso policial que fue resuelto gracias a las transformaciones biyectivas. Se trataba de una web de contenido pedófilo en la que los usuarios se registraban bajo pseudónimo. Al menos uno de ellos usó una foto auténtica como imagen de perfil, aunque distorsionada. La distorsión, una suerte de rotación en espiral, resultó ser una transformación biyectiva. A la policía le bastó invertir la transformación para identificarle y posteriormente detenerle.
Fue hace unos diez años. Lo recuerdo porque por aquel entonces andaba yo dando clase de álgebra lineal. Por desgracia, no logro encontrar la fuente.