En mi anterior entrada del Cuaderno de Cultura Científica Guía matemática para el cómic ‘Promethea’, sobre las referencias matemáticas que aparecen en Promethea (1999-2005), del guionista Alan Moore y el dibujante James H. Williams III, mencioné que en algunas partes del mismo aparecían “curvas hipotrocoides dibujadas con un espirógrafo”, como las que se pueden ver en la siguiente imagen.

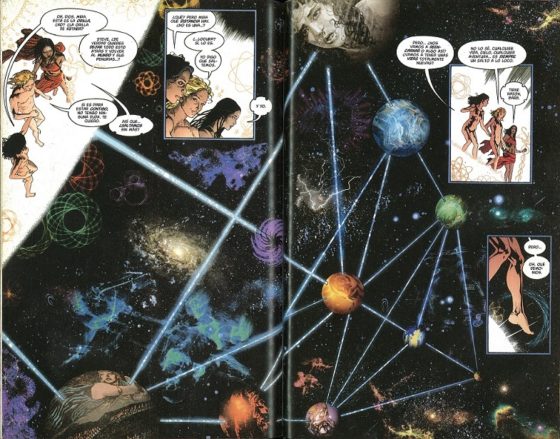
Si nos fijamos en las curvas que aparecen dibujadas en el cómic es posible que nos recuerden a los diseños geométricos realizados con un juguete llamado espirógrafo, con el que tal vez jugamos en nuestra infancia. Diseños geométricos como los que aparecen en la siguiente imagen.

O también los dibujos de esta otra imagen.

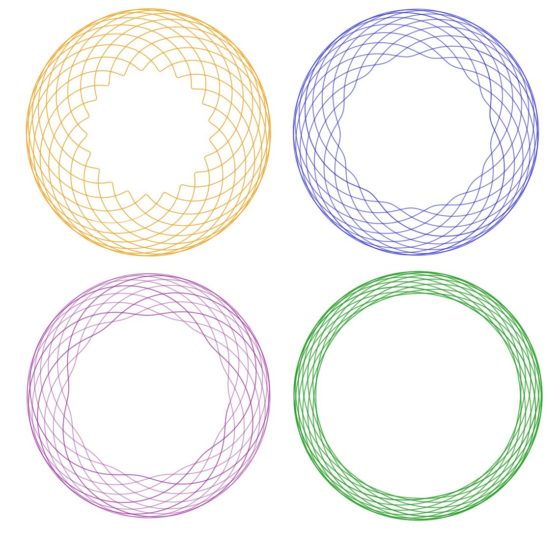
Estos diseños geométricos los he realizado con el Inspirograph, que es una réplica digital del espirógrafo desarrollada por el ingeniero canadiense Nathan Friend.

“Kate conocía a todos los tenderos y se llevaba bien con ellos. La verdulería la llevaban Eric y su mujer Mavis. No tenían hijos, pero eran amables con Kate y todas las navidades le compraban un regalo con el que –era increíble– siempre daban en el clavo. El año pasado le habían comprado un espirógrafo, y Kate lo había utilizado para confeccionar un logotipo para sus tarjetas de visita.”

[Katherine O Flynn, Lo que perdimos, Alfaguara, 2009]

El espirógrafo es un juguete con el que dibujar diseños geométricos que consisten en curvas cíclicas, en concreto, las curvas conocidas con los nombres de hipotrocoides (como los primeros dibujos que hemos trazado) y epitrocoides (como los segundos dibujos), que describiremos matemáticamente más adelante. Este juguete consiste en una serie de engranajes o ruedas dentadas –círculos o coronas circulares en la versión original y más sencilla, pero con formas más complejas en la actualidad–, de tal forma que al girar una rueda dentada sobre la otra, que permanece fija, se producen los diseños geométricos. El dibujo se realiza con un lápiz o rotulador cuya punta se coloca en uno de los agujeros que tiene el interior de la rueda dentada que se hace girar. La rueda dentada fija puede ser tanto una corona circular dentada, de forma que se puede girar la otra rueda dentada tanto por el exterior (generando las curvas epitrocoides), como por el interior (generando las curvas hipotrocoides), de las que solía haber dos en el juego, o un círculo dentado de diferentes tamaños sobre el que solo se puede hacer girar la otra por el exterior (generando hipotrocoides).

El espirógrafo fue creado por el ingeniero británico Denys Fisher (1918-2002) en los primeros años de la década de 1960. Animado por su familia y amigos, el ingeniero británico fundó Denys Fisher Toys (que en 1970 compraría la empresa Palitoy, la cual acabaría formando parte de Hasbro en 1991) y empezó a comercializar el juguete. Se presentó en la Feria Internacional de Juguetes de Nurenberg en 1965 y fue declarado juguete británico del año en 1967. Fue patentado en 16 países. La siguiente imagen es de la patente de 1966 en Estados Unidos.

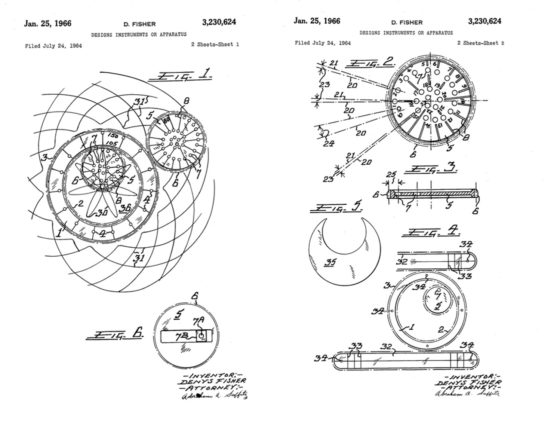
El juego fue todo un éxito. Además, evolucionó rápidamente incluyendo engranajes de formas variadas, que permitían diseños geométricos cada vez más sofisticados y originales. En 2013 la compañía de juguetes Kahootz relanzó el espirógrafo y ganó varios premios, como el Astra Best Toys for Kids de 2013, así mismo fue finalista a juguete del año en 2014.

Pero mencionemos algunos antecedentes de la creación del ingeniero británico Denys Fisher. En 1827 el ingeniero y arquitecto británico Peter Hubert Desvignes (1804-1883) diseñó un mecanismo que llamó “speiragraph” y que servía para dibujar complejas curvas de tipo espiral. El objetivo de este mecanismo era crear diseños que ayudasen a evitar las falsificaciones de los billetes.

El matemático, ingeniero eléctrico e inventor polaco Bruno Abakanowicz (1852-1900), quien inventaría mecanismos como el intégrafo, para representar la integral de una función definida gráficamente, y el parabológrafo, para trazar parábolas, inventó otro mecanismo con el nombre de “spirograh” (espirógrafo), entre 1881 y 1900, que también debía trazar curvas de tipo espiral (spiro + graph), aunque no he podido encontrar ninguna referencia directa del mismo.

El primer juguete precursor del espirógrafo fue el llamado “The Marvelous Wondergraph” con el que realizar diseños geométricos de curvas espirales, pero que pasó bastante desapercibido. En la publicación The Boy Mechanic apareció en 1913 un artículo explicando cómo construir tu propio wandergraph.

En la década de los años 1930 se comercializó otro juguete para trazar diseños geométricos de curvas, llamado “Hoot-Nanny, The Magic Desiner”, que tuvo más éxito que el anterior y se vendió hasta la década de los años 1950. En la siguiente imagen vemos las instrucciones originales del juguete, con algunas de las curvas que podían trazarse con el mismo. Además, hay un simulador en la red del Hoot-Nanny, con el que podéis divertiros trazando curvas curiosas.

Aunque el juguete espirógrafo del ingeniero británico Denys Fisher fue el que más éxito alcanzó, quizás por la sencillez de su diseño y su manejo, por lo que también trazaba curvas más sencillas, o tal vez porque en los años 60 la sociedad estaba más abierta a este tipo de imágenes geométricas, ya que era el tiempo de la psicodelia y del arte pop.

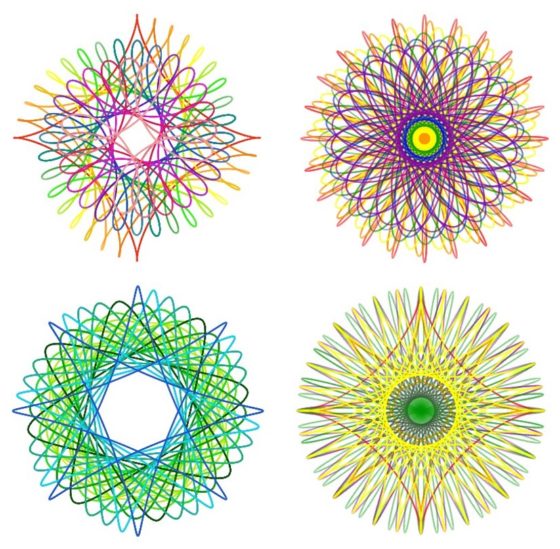
Pero vayamos a las curvas geométricas que dibuja el espirógrafo, las hipotrocoides y epitrocoides, que son dos tipos particulares de curvas cíclicas o “ruletas”. Las curvas cíclicas son las curvas planas descritas por la trayectoria de un punto que pertenece a una curva plana (o relacionado con ella) que rueda, sin deslizarse, sobre otra curva plana. A la familia de las curvas cíclicas pertenecen la cicloide, las trocoides, las epicicloides, las hipocicloides, epitrocoides, hipotrocoides y las involutas.

La cicloide es la curva que describe un punto que está en el borde de una rueda circular, es decir, el punto de una circunferencia, que rueda, sin deslizarse, a lo largo de una recta.

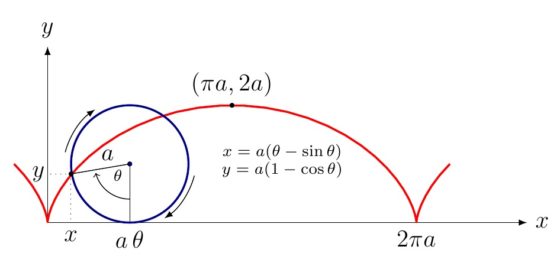
Esta curva, como las demás que se citan aquí, ya era conocida en la antigüedad, pero fue ampliamente estudiada en el siglo XVII por grandes matemáticos como el francés Marin Mersenne (1588-1648), quien dio la primera definición matemática precisa, el italiano Galileo Galilei (1564-1642), quien estudió la curva durante cuarenta años y a quien le debemos su nombre (que viene de las palabras griegas kuklos, de la que deriva ciclo y que significa círculo, y eidos, que significa forma o imagen), el francés Gilles de Roverbal (1602-1675), quien calculó el área debajo de la curva, el italiano Evangelista Torricelli (1607-1647), Blaise Pascal (1623-1662), que tiene una curiosa relación con la cicloide (puede leerse en la entrada Blaise Pascal, Dios y la cicloide), Christiaan Huygens (1629-1695), quien descubriría que la cicloide es la curva tautócrona, es decir, aquella para la cual el tiempo que tarda una bola en recorrer la cicloide invertida, sin deslizamiento, hasta llegar al punto más bajo de la curva es independiente de la altura desde la que se dejó caer la bola, y utilizó esta propiedad para construir el péndulo cicloidal, el francés Girard Desargues (1591-1661), el matemático alemán Gottfried Wilhelm Leibniz (1646-1716), o el matemático suizo Johann Bernoulli (1667-1748), quien descubrió que la cicloide era la curva braquistócrona, es decir, la curva de recorrido más rápido de una bola que se desplaza de un punto a otro más bajo por el efecto de la gravedad, entre muchos otros.

Una cita literaria conocida en la que se menciona a la cicloide y su condición de curva tautócrona es Moby Dick (1851), del escritor estadounidense Hermann Melville (1819-1891):

Algunos marineros viejos y cínicos acostumbran, durante las guardias de noche, introducirse en ellas [las dos ollas de la refinería del barco] y enrollarse en su interior para dormir un rato. Mientras están dedicados a la tarea de lustrarlas –un hombre en cada olla, hombro con hombro– se transmiten muchas comunicaciones confidenciales, por encima de los labios de hierro. El sitio es propicio, también, para la meditación matemática profunda. En la olla izquierda del Pequod, mientras hacía circular dirigentemente la esteatita frente a mí, me sorprendió indirectamente el hecho notable de que en geometría todos los cuerpos que se deslizan en el cicloide, mi esteatita por ejemplo, descienden de cualquier punto exactamente en el mismo tiempo.

Por otra parte, se denomina curva trocoide a la curva que describe un punto conectado con una rueda circular, ya sea porque pertenece al interior de la misma, a su circunferencia o siendo exterior al círculo está conectado con este, que rueda, sin deslizarse, sobre una línea recta. Por lo tanto, la cicloide es una curva trocoide (término que viene de las palabras griegas trhokos, que significa rueda, y eidos, que significa forma o imagen) en la que el punto está sobre la circunferencia de la rueda circular. Si el punto es interior se habla de cicloide reducida y si es exterior de cicloide alargada.

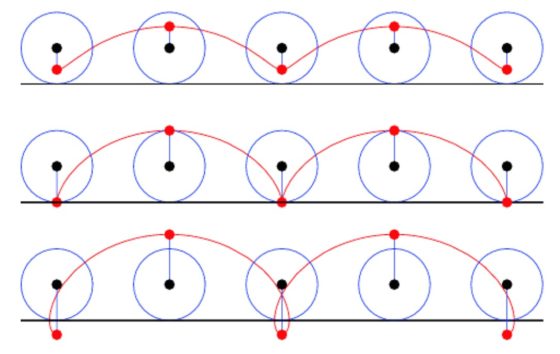
En el espirógrafo clásico hay dos piezas muy alargadas de forma que la parte central es recta, por lo cual, al girar una de las ruedas dentadas por esta parte se obtiene una cicloide reducida.

La curva epicicloide es la trayectoria de un punto de una circunferencia que rueda, sin deslizarse, por el exterior de una circunferencia fija. En función de la relación que existe entre los radios de ambas circunferencias se obtendrán diferentes curvas. Por ejemplo, si ambos radios son iguales se obtiene una cardioide, si el radio de la circunferencia que rueda es la mitad (1/2) del radio de la rueda fija, la curva es una nefroide.

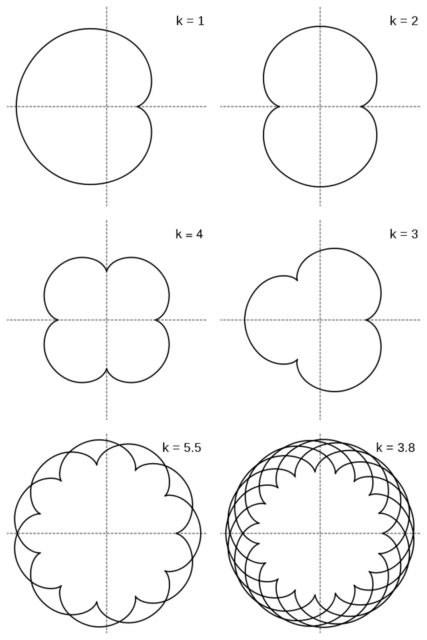
Por otra parte, si la circunferencia que rueda lo hace por el interior de la cincunferencia fija la curva que se obtiene es una hipocicloide. Si la relación entre los radios de las circunferencias pequeña –la que rueda– y grande –la que esta fija– es 1/3 se obtiene la curva denominada deltoide, si es 1/4 la curva generada es una astroide y de nuevo en función de esa relación se obtienen diferentes curvas.

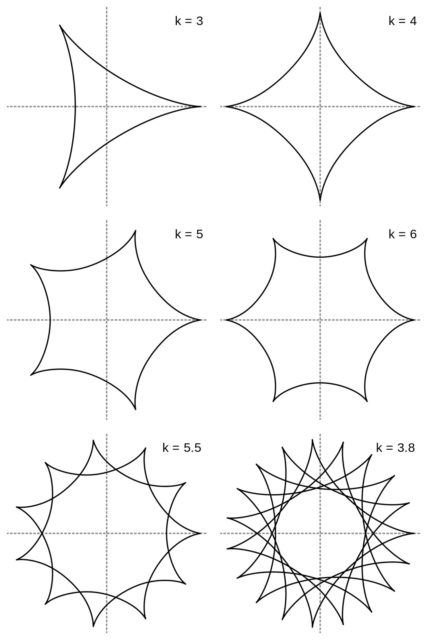
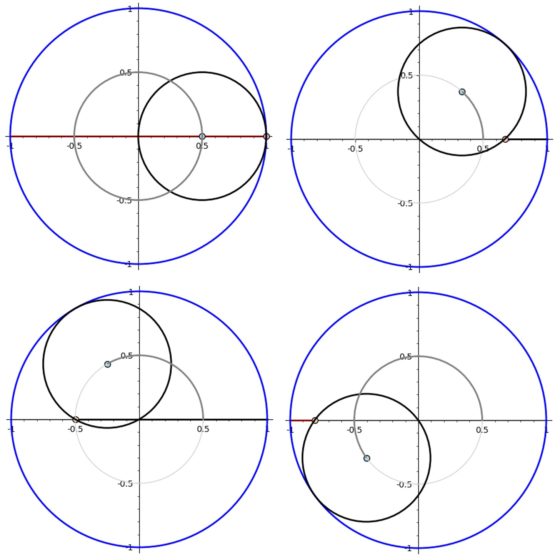
No hemos mencionado intencionadamente cual es la curva que se obtiene cuando la relación entre los radios de ambas circunferencias es 1/2, ya que esta es una recta, conocida con el nombre de “línea de La Hire”, y que es una forma de obtener un movimiento lineal a partir de un movimiento circular. Como se ve en la siguiente imagen, cuando la circunferencia móvil recorre la mitad del camino, el punto de la circunferencia que gira (color crema en la imagen) recorre el diámetro de la circunferencia fija, y lo vuelve a recorrer en la otra mitad del giro.

En la antigüedad la humanidad pensaba que la circunferencia era una figura geométrica perfecta, relacionada con lo divino, por lo que postularon que el movimiento de los planetas era circular alrededor de la Tierra. Dos de los grandes defensores de este modelo fueron Aristóteles (384–322 a.n.e) y Claudio Ptolomeo (aprox. 100-170). Sin embargo, muchos pensadores postularon que el Sol era el centro natural –el primero en proponerlo fue Aristarco de Samos (aprox. 310-230 a.n.e.)– y se dieron cuenta de que entonces, según las observaciones astronómicas, el movimiento de los planetas alrededor del Sol no podía ser circular. Por lo tanto, introdujeron las curvas epicicloides e hipocicloides para producir curvas que se adaptaran al movimiento observado de los planetas. Y como estos tampoco acababan de describir perfectamente los movimientos, empezaron a introducir curvas más complejas relacionadas con las anteriores. Las dos teorías sobre el movimiento de los planetas, circular o mediante curvas derivadas de epicicloides e hipociclodides, fueron rivales hasta que Johannes Kepler (1571-1630) demostró, a partir de las observaciones de Tycho Brahe (1546-1601), que la órbita de Marte era elíptica, con el Sol en uno de sus focos. Posteriormente, Isaac Newton (1643-1727) demostraría matemáticamente que la órbita de un cuerpo alrededor de un campo gravitatorio son secciones de cónicas.

El estudio de las epicicloides e hipocicloides se reinició en el Renacimiento. Estas curvas fueron estudiadas por Alberto Durero (1471-1528), Girard Desargues, Christian Huygens, Gottfried Wilhelm Leibniz, Isaac Newton, Jacob Bernoulli (1654-1705), Phillipe de La Hire (1640-1718), Johann Bernoulli, Daniel Bernoulli (1700-1782) o Leonhard Euler (1707-1783), que también estudiarían las siguientes curvas que vamos a mostrar en esta entrada del Cuaderno de Cultura Científica.

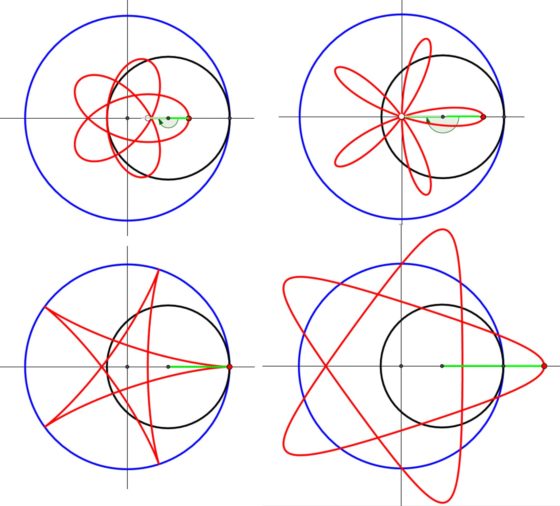
Las últimas curvas cíclicas que vamos a mostrar aquí son las generadas por el espirógrafo clásico, las epitrocoides e hipotrocoides. Una curva epitrocoide es la trayectoria que describe un punto, conectado a un círculo que rueda, sin deslizamiento, sobre el exterior de una circunferencia fija. Si el punto está en el interior del círculo que rueda se obtiene una epitrocoide como algunas de las obtenidas en el espirógrafo clásico (primera curva de la siguiente imagen), si el punto está en la circunferencia es una epicicloide (segunda curva de la imagen), mientras que si el punto es exterior al círculo que rueda (que podemos considerar conectado al centro por un segmento fijo para que ruede con el círculo) se obtiene una epitrocoide que podemos dibujar fácilmente con el ordenador, pero no con el espirógrafo clásico (tercera curva de la imagen).

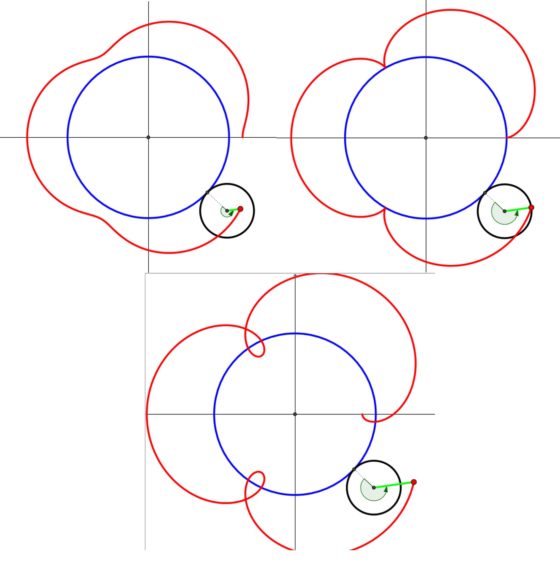
En la siguiente imagen podemos ver una epitrocoide dibujada con el espirógrafo clásico, con una rueda dentada rodando alrededor de otra rueda dentada fija.

Mientras que una curva hipotrocoide es la trayectoria que describe un punto, conectado a un círculo que rueda, sin deslizamiento, sobre el interior de una circunferencia fija. De nuevo el punto conectado al círculo que rueda puede ser interior, de la circunferencia o exterior.

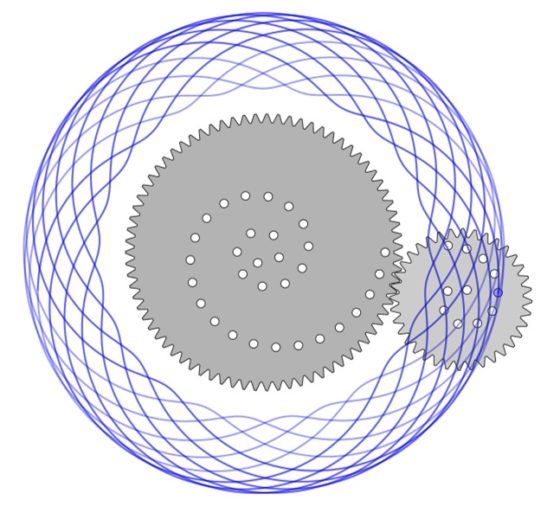
De la misma forma que antes, podemos ver una hipotrocoide dibujada con el espirógrafo clásico, con una rueda dentada rodando en el interior de una corona circular dentada fija.

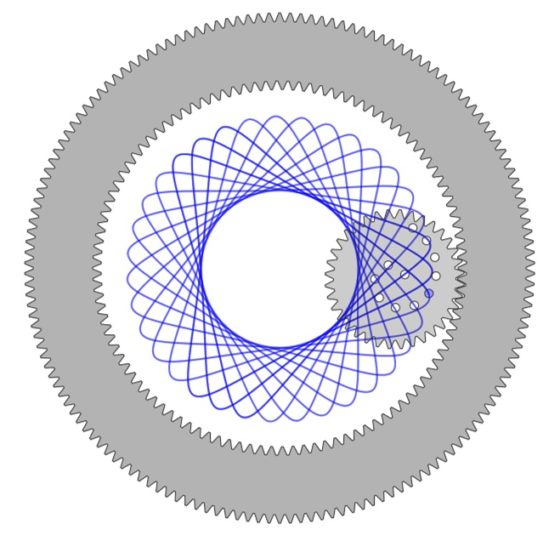
Un ejercicio bonito, relacionado con todas estas curvas cíclicas, es la obtención de las ecuaciones paramétricas de las mismas. Por ejemplo, las ecuaciones paramétricas de las hipotrocoides son:

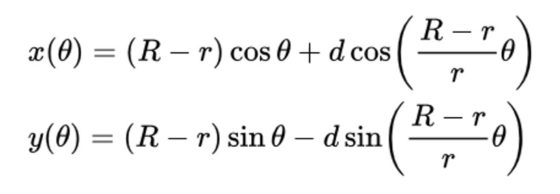
donde R es el radio de la circunferencia fija exterior, r el radio del círculo interior que rueda y d la distancia al centro del círculo que gira del punto cuya trayectoria estamos considerando (que describe la hipotrocoide). Sin embargo, no lo resolveremos en esta entrada, lo dejaremos para aquellas personas a las que les apetezca enfrentarse al mismo.

Para terminar, mencionaremos que también existen artistas contemporáneos, como ocurrió con Alan Moore y James H. Williams III, autores del cómic Promethea, que han quedado fascinados por la belleza de los diseños de las curvas cíclicas generadas con el espirógrafo. Un ejemplo es la artista estadounidense Robin P. Schlacter, quien utiliza hipotrocoides en muchas de sus obras.

Bibliografía

1.- Wikipedia: Spirograph .

2.- Wolfram Mathworld: Spirograph

3.- Nathan Friend, Inspirograph

4.- Toy tales: Spirograph

5.- J. Dennis Lawrence, A catalog of special plane curves, Dover Publications, 1972.

6.- José Manuel Álvarez Pérez, Curvas en la historia 1 y 2, Nivola, 2006.

7.- Wikipedia: Hypotrochoid

8.- Wikipedia: Epitrochoid

9.- Raúl Ibáñez, Construcción de curvas planas, Un paseo por la Geometría 1997/1998.

10. Página web de la artista Robin P. Schlacter.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica