El amor ha sido el opio de las mujeres, como la religión el de las masas. Mientras nosotras amábamos, los hombres gobernaban
El matemático Steven H. Strogatz es especialista en el estudio de redes complejas y divulgador científico. En 1988 (ver [1]) publicó un artículo en el que proponía modelizar una determinada situación amorosa —entre, por ejemplo, Romeo y Julieta— usando ecuaciones diferenciales.

Tras este artículo, muchas otras personas han escrito sobre este tema, es decir, sobre la modelización matemática de algunas situaciones románticas, intentando prever la evolución en el tiempo de ese vínculo amoroso. Vamos a explicar uno de estos modelos.
Supongamos que R(t) denota el amor de Romeo por Julieta en el tiempo t. Si R(t) tiene valor positivo significa que él la adora, y si es negativo no la soporta demasiado. Del mismo modo, J(t) denota el cariño de Julieta hacia Romeo en el instante t.
Una manera de plantear las ecuaciones que gobiernan la evolución en el tiempo de la relación entre ambos —un posible modelo para esta relación amorosa—es la siguiente:
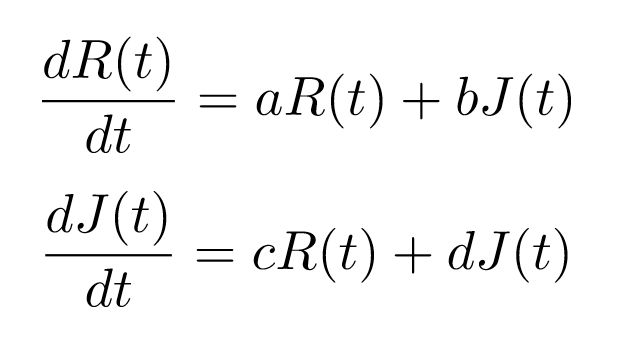
donde las constantes a y b determinan el carácter romántico de Romeo, y c y d la manera de querer de Julieta. Que dR(t)/d(t) sea positivo significa que R(t) aumenta al pasar el tiempo, y sucede lo contrario si es negativo.
¿Qué valores tienen las constantes a, b, c y d? Aunque su valor importa —como veremos más adelante— lo realmente relevante es el signo que poseen cada una de ellas. Que a sea positivo significa que Romeo se siente estimulado por sus propios sentimientos, y que sea negativo denota lo contrario. Si pensamos en b, el que sea positivo expresa que Romeo se siente animado por los sentimientos de Julieta, mientras que un valor negativo significaría que se desanima cuando Julieta siente interés por él. Se puede hacer una interpretación similar de c y d con respecto a la evolución del amor de Julieta por Romeo.
A Strogatz y su alumnado se les ocurrió clasificar los posibles “estilos románticos” del siguiente modo:
-
Si a y b son ambos positivos, hablamos de un castor ansioso: Romeo se siente estimulado tanto por sus propios sentimientos como por los de Julieta.
-
Si a es positivo y b es negativo nos encontramos ante un nerd narcisista: Romeo desea más de lo que siente, pero le asustan los sentimientos de Julieta.
-
Si a es negativo y b es positivo tropezamos con un amante cauteloso: Romeo se retrae ante sus propios sentimientos, pero el cariño que le profesa Julieta lo anima.
-
Si a y b son ambos negativos, nos encontramos con un ermitaño: Romeo huye de sus propios sentimientos y también de los de Julieta.
La manera en el que el amor de Julieta varía con el tiempo se puede clasificar de la misma manera: d se corresponde con a en la ecuación de Romeo, y c con b. Existen diferentes tipos de relaciones dependiendo de los valores de las constantes a, b, c y d. Algunos de ellos se muestran a continuación (pueden encontrarse los detalles en [3], [4] y [5]).
Pasión versus indiferencia
Romeo y Julieta se comportan como “polos opuestos” cuando c=–b y a=-d. las ecuaciones quedan entonces del modo
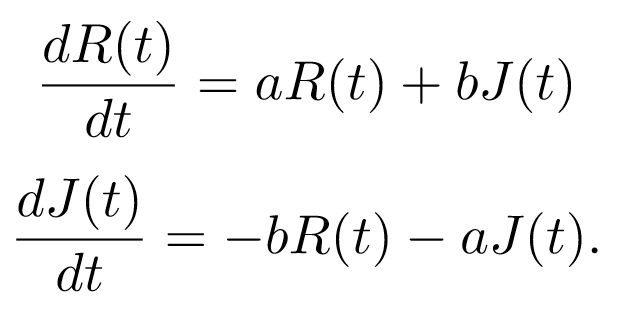
Estas relaciones pueden suceder de dos maneras:
-
Cuando coinciden un castor ansioso y una ermitaña (o viceversa), la evolución en el tiempo de la relación depende de los sentimientos que se priorizan, los propios (|a|>|b|) o los ajenos (|a| < |b|). Si Romeo prioriza sus propios sentimientos, la pareja terminará en desacuerdo: uno por siempre enamorado y la otra absolutamente indiferente. Y, en el caso opuesto, la pareja terminará en un ciclo interminable de amor y desamor que sucederán —cada uno de ellos— aproximadamente una cuarta parte del tiempo.
-
Cuando coindicen un nerd narcisista y una amante cautelosa (o viceversa), de nuevo todo depende de la prioridad dada a los sentimientos propios o ajenos. Si |a|>|b|, la pareja finalizará enamorada o en guerra perpetua. Y si |a| < |b|, terminarán en un eterno ciclo de amor y desamor.
Así que eso de que “polos opuestos” se atraen, no parece que funcione demasiado bien…
Embriagados por los sentimientos ajenos
¿Y si Romeo y Julieta solo se dejan llevar por los sentimientos del otro? Es decir, ¿qué sucede si a=d=0? El sistema de ecuaciones quedaría en este caso del modo siguiente:
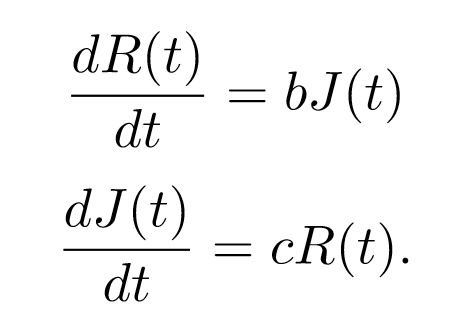
Y tres casos son posibles:
-
Si coinciden dos amantes cautelosos (b>0 y c>0), el resultado es el mismo que el de caso del nerd narcisista y la amante cautelosa con |a|>|b|.
-
Si tenemos dos nerds narcisistas (b < 0 y c< 0), el resultado obtenido es similar al del castor ansioso y la ermitaña con |a|>|b|.
-
Y si coinciden un nerd narcisista y una amante cautelosa (o viceversa, es decir, bc < 0), la pareja se verá abocada a un interminable ciclo de amor y desamor.
Por cierto, el “modelo de Shakespeare” correspondería al caso en el que a=d=0 y b y c son positivos, es decir, al de dos amantes cautelosos.
Y el modelo de Strogatz —el que propone en [1]— supone que a=d=0, b es negativo y c es positivo, es decir, estudia la relación entre un nerd narcisista y una amante cautelosa. En este caso, Romeo es un amante caprichoso: cuanto más lo quiere Julieta, menos ganas tiene Romeo de cortejarla. Y cuando Julieta pierde el interés por él, Romeo empieza a encontrarla extraordinariamente atractiva. Julieta, por el contrario, se deja llevar por los sentimientos de Romeo: su deseo crece cuando él la adora, y se enfría cuando él la ignora. Como ya sabemos, esta triste historia evoluciona como un interminable ciclo de amor y odio…
¿Cómo evolucionan otros posibles casos? ¿Te atreves a dar un modelo alternativo al planteado arriba?
Referencias
[1] Steven H. Strogatz, Love Affairs and differential equations, Mathematics Magazine 61, 35, 1988
[2] Steven H. Strogatz, Loves Me, Loves Me Not (Do the Math), Opinionator, 2009
[3] Omstavan, Love Affairs: A mathematical model using Differential equations!, Steemit, 2018
[4] Fabian Dablander, Love affairs and linear differential equations, R-bloggers, 2019
[5] Isaac Elishakoff, Differential Equations of Love and Love of Differential Equations, Journal of Humanistic Mathematics 9 (2), 2019, 226-246
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

Pablo Rodríguez
Me permito añadir a la lista Modeling love dynamics, de Sergio Rinaldi. Un curiosísimo libro sobre este asunto que utiliza romances de la literatura y el cine como ejemplos.