Sí, Amelia quiere explorar el desierto. Ha conseguido el patrocinio de una millonaria que le impone unas cuantas reglas para que agudice su ingenio. Las explicamos a continuación.
Amelia tiene a su disposición una cantidad ilimitada de gasolina almacenada en el lugar de salida, en el límite del desierto.
Para realizar su viaje, dispone de un jeep en el que puede transportar como máximo, en cada momento, una unidad de combustible. Con cada unidad de gasolina puede viajar una unidad de distancia; se supone que el consumo de combustible es constante.
En cualquier momento del viaje, Amelia puede dejar cualquier cantidad de combustible en un depósito para poder recogerlo más tarde al volver a pasar por allí. La mecenas le exige, además, que siempre que el jeep comience a salir del desierto debe regresar necesariamente al punto de partida.
Con todas estas normas impuestas, la pregunta es: ¿hasta dónde puede llegar Amelia en su paseo por el desierto?
Vamos a intentar ver que puede llegar tan lejos como quiera, solo con un poco de estrategia por su parte. Para ello, vamos a explicar lo lejos llegaría realizando tres viajes –saliendo tres veces del punto de partida– para describir después el caso general.
La estrategia de Amelia si realiza tres salidas
Amelia sale de la base una unidad de gasolina en el depósito del jeep y conduce 1/6 de unidades de distancia. Es decir, ha consumido la sexta parte del combustible. Deja 2/3 de unidades de combustible en un depósito, y regresa al punto de partida con el 1/6 de combustible que le queda.
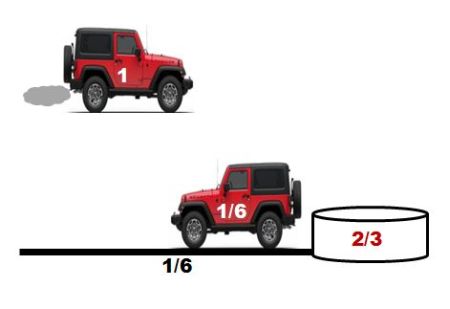
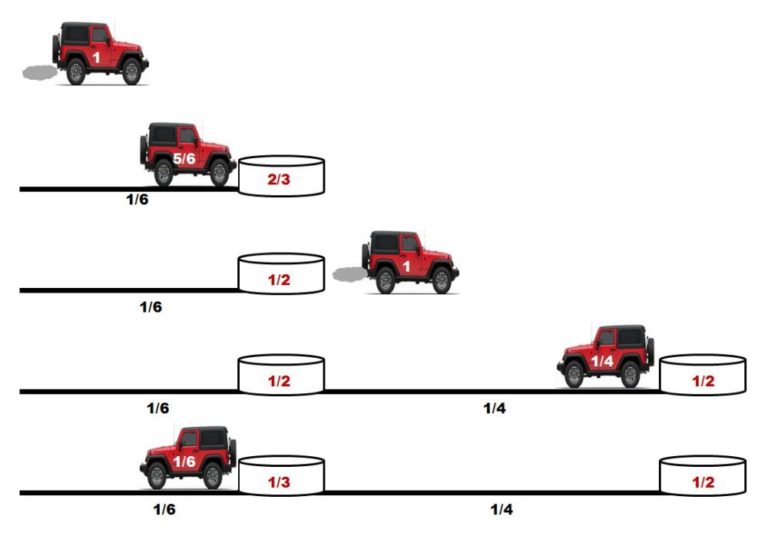
Amelia vuelve a cargar el depósito del jeep al máximo –es decir con una unidad de combustible– y conduce 1/6 de unidades de distancia. Ha gastado 1/6 de unidades de gasolina; llena el depósito del coche con 1/6 de combustible tomado del depósito, y vuelve a adentrarse en el desierto, dejando en el primer depósito 1/2 de unidades de fuel. Desde ese punto conduce 1/4 de unidades de distancia y deposita 1/2 unidad de gasolina en un segundo recipiente. Le quedan 1/4 de unidades de fuel, lo justo para llegar al primer bidón. De ese recipiente toma 1/6 de unidades de combustible –es decir, deja el primer bidón con 1/3 de unidades de fuel– y llega a la base con el depósito del coche vacío.
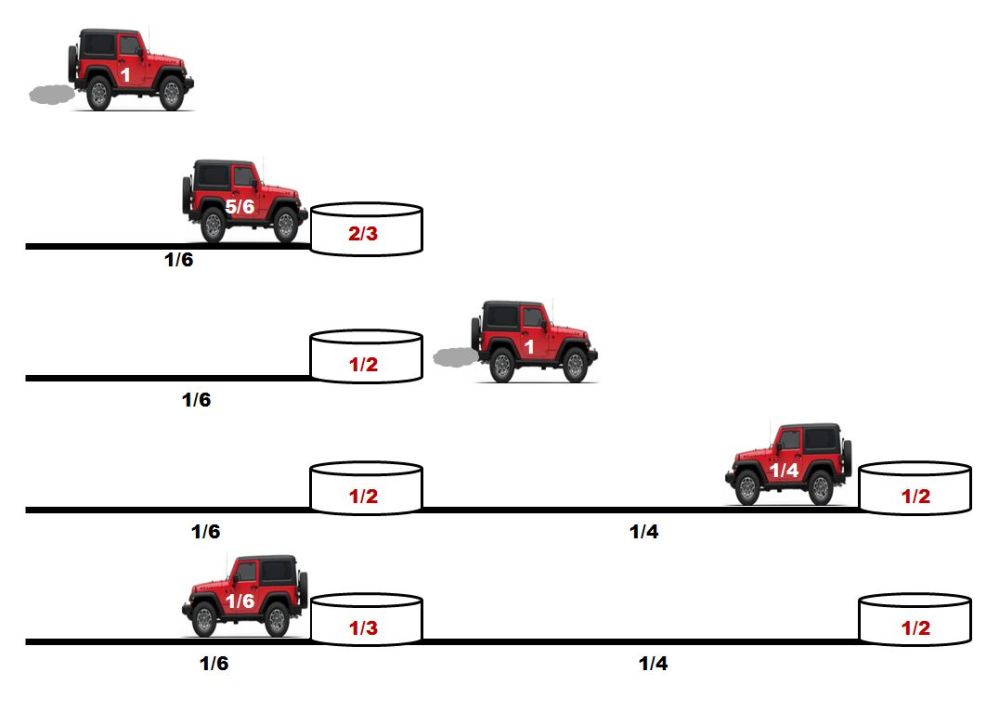
Amelia carga el coche con el máximo de gasolina, llega al primer bidón y utiliza 1/6 de combustible para volver a llenar el depósito del jeep –así, en el primer depósito, deja 1/6 de unidades de gasolina–. Llega al segundo recipiente tras recorrer 1/4 de unidades de distancia, y allí vuelve a llenar el vehículo con fuel, dejando en el segundo depósito 1/4 de unidades de combustible, y continúa su viaje hacia el interior del desierto. Tras recorrer 1/2 unidad de distancia, da la vuelta, llega al segundo recipiente gastando todo el combustible que le queda, usa el fuel del segundo recipiente para llegar al primero y de nuevo toma la gasolina del primer bidón para regresar al punto de partida.
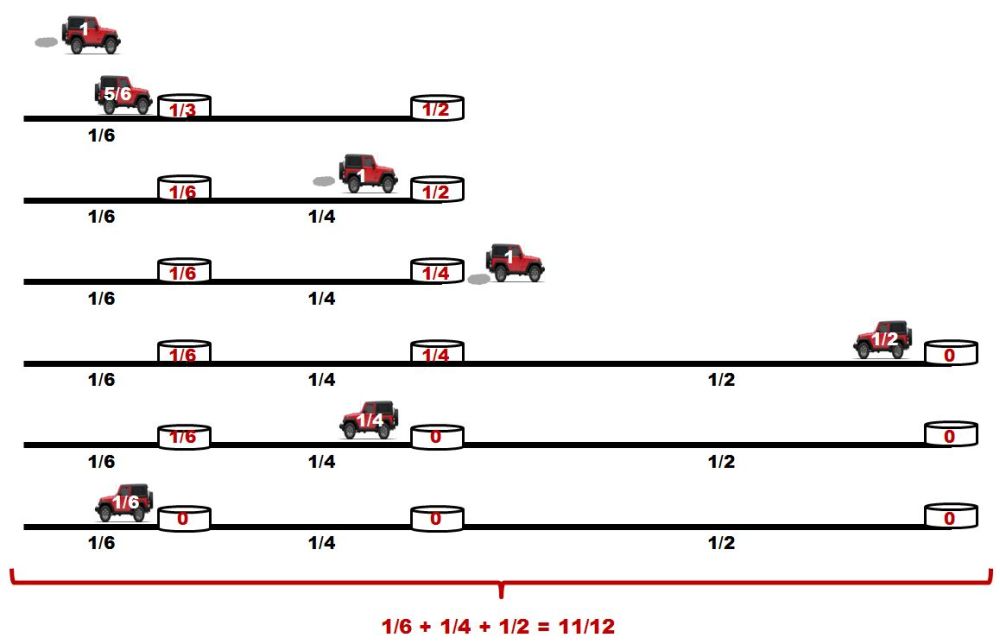
Así, con estas tres idas y vueltas, Amelia se ha adentrado en el desierto 11/12 de unidades de distancia.
Entendiendo el caso general
La estrategia utilizada por Amelia con tres salidas desde el límite del desierto puede generalizarse para cualquier n:
-
El jeep realiza n viajes de ida y vuelta.
-
En la primera salida, viaja 1/(2n) de unidades de distancia, deja (n − 1)/n unidades de gasolina en el primer depósito, quedándose con el combustible justo para llegar a la base.
-
En cada una de las n − 1 siguientes salidas, y en dirección hacia el interior del desierto, Amelia va tomando de cada depósito el combustible necesario para llenar al máximo el jeep y llegar al siguiente depósito. Y al regresar, va tomando solo la gasolina suficiente para llegar al depósito anterior.
-
Esta operación la puede realizar n veces, dejando en su último viaje todos los bidones vacíos, y habiendo recorrido en la dirección del desierto
1/2 + 1/4 + 1/6 + … + 1/(2n) = 1/2 (1 + 1/2 + 1/3 + … + 1/n)
de unidades de distancia.
Recordemos que 1 + 1/2 + 1/3 + … + 1/n es el n-ésimo número armónico,la suma parcial n-ésima de la serie armónica, que es una serie divergente.
¿Y que tiene esto que ver con el viaje de Amelia? Si la exploradora utiliza la estrategia anteriormente descrita, podrá adentrarse en el desierto todo lo que desee, porque para n suficientemente avanzado,
1/2 (1 + 1/2 + 1/3 + … + 1/n)
es tan grande como se desee… Como el desierto, sea cual sea el que ha elegido Amelia, tiene dimensiones finitas, la exploradora puede recorrerlo por completo. Solo necesita suficiente tiempo –que no sobrepase su tiempo de vida–: Amelia completará su aventura. Aunque es probable que arruine a su mecenas y, sobre todo, que desperdicie un combustible precioso de manera un tanto caprichosa…
Más información:
-
Jeep problem, Wikipedia
-
Jeep problem, Wolfram Math World
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
Albert Galobart Roca
Si realiza un cuatro viaje ¿qué cantidad de gasolina llena del primer depósito?. Está vacio!
Marta Macho Stader
Albert, en el primer depósito hay toda la gasolina que quiera:
«Amelia tiene a su disposición una cantidad ilimitada de gasolina almacenada en el lugar de salida, en el límite del desierto.».