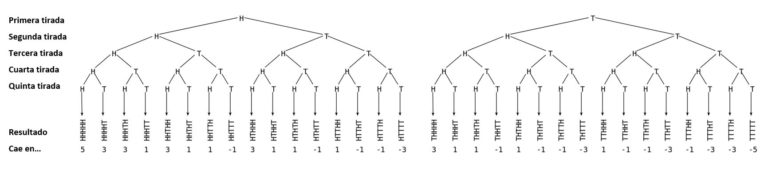
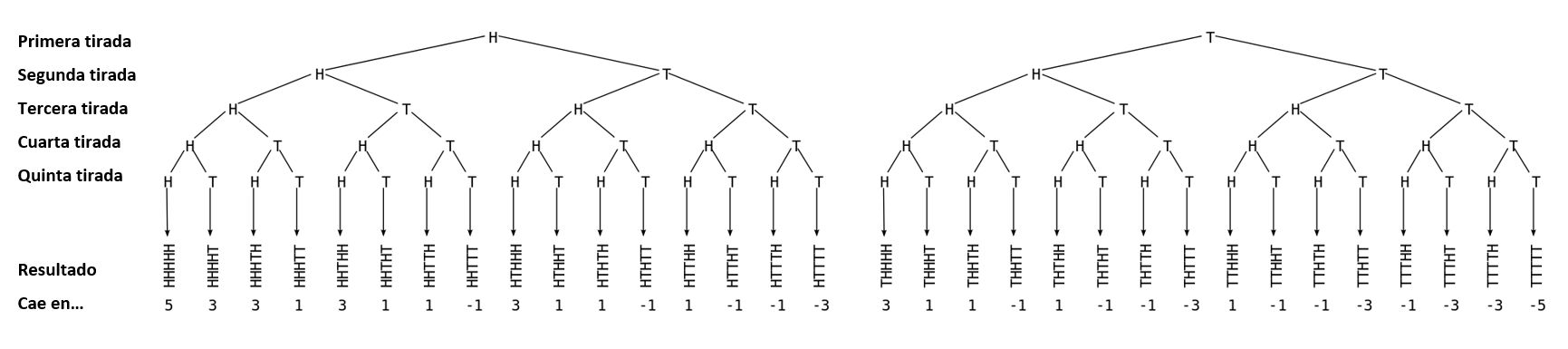
Pensemos en un suceso con dos posibles resultados, por ejemplo el de lanzar una moneda al aire. Si la moneda no está trucada, la probabilidad de que caiga cara o cruz es la misma, de 1/2. Si estudiamos la sucesión de resultados obtenidos al repetir sucesivamente este experimento –y que son estadísticamente independientes– obtenemos un camino o paseo aleatorio, en este caso, de dimensión 1. El paseo consistiría en dar un paso a la izquierda o a la derecha, dependiendo de que la moneda mostrara cara o cruz.

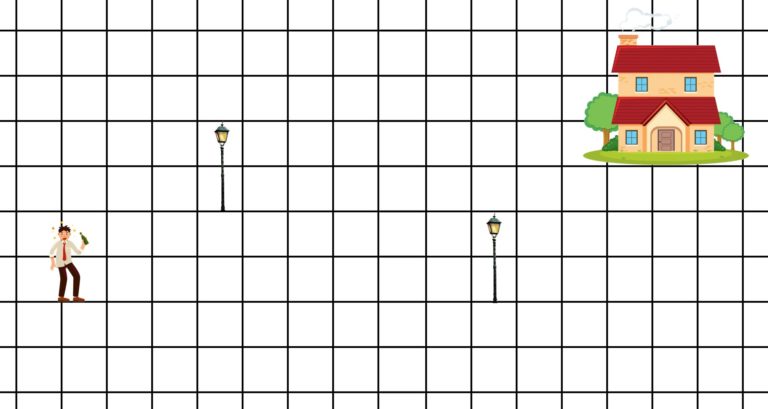
Añadamos ahora una dimensión más. Pensemos en Juan López, que intenta llegar a su casa tras una noche de fiesta en la que no ha moderado su consumo de alcohol. Debe recorrer la distancia entre el lugar en el que se encuentra y su casa, pero está bastante aturdido y va dando algún que otro traspiés, cambiando a veces la dirección de su marcha. Podemos imaginar que Juan está caminando aleatoriamente por su ciudad, cuyas calles forman un retículo de dimensión 2. En cada cruce, Juan decide –en realidad, con lo desorientado que está, es el azar el que decide por él– una de las cuatro posibles direcciones en cada cruce. Por supuesto, puede elegir también aquella dirección por la que ha venido; cualquier elección –norte, sur, este y oeste– tiene la misma probabilidad de 1/4. Este sería un paseo aleatorio bidimensional. La pregunta es: ¿conseguirá Juan a su casa?

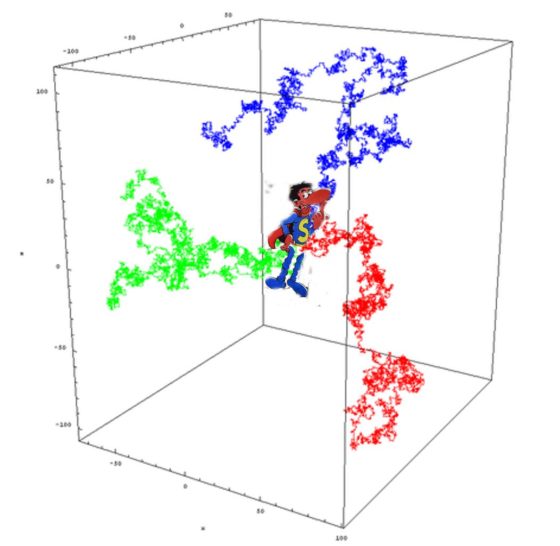
Imaginemos una última situación. Unas semanas más tarde Superlópez –el alter ego de Juan López– vuelve de una fiesta provisto con su traje de superhéroe. Tampoco ha sido capaz de moderarse. Intenta regresar a su casa para descansar. Pero esta vez, al poder volar, su recorrido es aún más complejo. Podemos imaginar a Superlópez volando aleatoriamente por un retículo de tres dimensiones; en cada cruce de cada cubo de vértices con coordenadas enteras, Superlópez tiene seis posibles caminos equiprobables a seguir. ¿Llegará el superhéroe ebrio y desorientado hasta su casa?

Obviamente, la noción de paseo aleatorio se puede generalizar a retículos de cualquier dimensión. En 1921, el matemático George Pólya demostró el siguiente resultado:

Sea p(d) la probabilidad de que un paseo aleatorio sobre un retículo de dimensión d regrese a su punto de partida. Se verifica que:

p(1) = p(2) = 1 y p(d) < 1 si d > 2.

Además, Watson (1939), McCrea y Whipple (1940), Domb (1954) y Glasser y Zucker (1977) demostraron que:

p(3) = 0,34053732955099914282627318443…

Al aumentar el número de dimensiones d del retículo, p(d) va disminuyendo, se hace más difícil regresar al punto de partida (Ver Sloane).

¿Qué enseñanza puede obtener Juan López de estos resultados? En primer lugar, que debe moderar su ingesta de alcohol. En el caso de que la fiesta se “desmadre” y sus facultades se vean afectadas, más vale que no saque su disfraz de Superlópez. ¿Por qué? Porque la probabilidad de llegar a su casa caminando –aunque sea con dificultad– como Juan López es de 1. Sin embargo, cuando cambia a su personalidad de Superlópez e intenta regresar volando, todo se complica. Realizando sus desplazamientos aleatorios en dimensión 3, la probabilidad de llegar a casa es menor de 0,35. Volando con su personalidad de superhéroe se arriesgaría a vagar al azar sin encontrar su añorada morada…

Referencias

Bruno Winckler, Recueil de blagues mathématiques et autres curiosités, Ellipses, 2011 (leído y adaptado de este libro)

Eric W Weisstein, Pólya’s Random Walk Constants, From MathWorld–A Wolfram Web Resource

N. J. A. Sloane, Decimal expansion of probability that a random walk on a 3-D lattice returns to the origin, The On-line Encyclopedia of Integer Sequences

G. Pólya, Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Straßennetz, Mathematische Annalen 84 (1921) 149-160

G. N. Watson, Three Triple Integrals, Quart. J. Math. 2 10 (1939) 266-276

W. H. McCrea and F. J. W. Whipple, Random Paths in Two and Three Dimensions, Proc. Roy. Soc. Edinburgh 60 (1940) 281-298

C. Domb, On Multiple Returns in the Random-Walk Problem, Proc. Cambridge Philos. Soc. 50 (1954) 586-591

M. L. Glasser and I. J. Zucker, Extended Watson Integrals for the Cubic Lattices, Proc. Nat. Acad. Sci. 74 (1977) 1800-1801

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.