Esta es la segunda entrega de esta pequeña serie de entradas del Cuaderno de Cultura Científica dedicadas al humor matemático que empezó con la entrada ¿Saben aquel que dice … matemáticas? (I).
Como decíamos en la entrega anterior, este tipo de humor no se define únicamente por el hecho de que se centre en las matemáticas o en las personas que desarrollamos esta ciencia, sino que el pensamiento matemático y la propia esencia de la ciencia de Pitágoras (investigación matemática, demostraciones, razonamiento matemático, áreas de las matemáticas, conceptos matemáticos, problemas, etc.) constituyen elementos fundamentales en el mismo.

Al igual que en la anterior entrada, vamos a empezar con algunos chistes cortos. El primero es un chiste sobre la esencia de las matemáticas.
Las matemáticas están formadas por un 50% de fórmulas, un 50% de demostraciones y un 50% de imaginación.
En la misma línea del chiste de la entrega anterior sobre el motivo por el cual se suicidó el libro de matemáticas, “porque tenía demasiados problemas”, tenemos los siguientes que responden a la pregunta “¿cuál es el colmo de …?” o “¿Qué es lo peor que le puede pasar a …?”.
a. ¿Cuál es el colmo de una matemática? Morir de cálculos.
b. ¿Qué es lo peor que le puede pasar a un matemático? Que no cuenten con él.
c. ¿Qué es lo peor que le puede pasar a una matemática? Que tenga los días contados.
d. ¿Cuál es el colmo de un matemático? Tener un hijo cateto.
e. ¿Cuál es el colmo de una profesora de matemáticas? Equivocarse cada dos por tres.
f. ¿Cuál es el colmo de un profesor de matemáticas? Que no pueda sacar la raíz de una planta.
El siguiente chiste corto está relacionado con la resta y los números negativos.
Era un hombre con una personalidad tan negativa, tan negativa, tan negativa, que cuando llegaba a una fiesta, los invitados empezaban a mirarse extrañados y se preguntaban quien se había ido.
O este chiste que he encontrado en la página Matemáticas en tu mundo, de Jose María Sorando.
Un filósofo, un biólogo, un físico y un matemático charlaban en la barra de un bar. A mitad de la conversación, 2 personas entran en una camioneta aparcada frente al bar y al cabo de un rato salen 3.
– “¡Pero esto es imposible!”, dice el filósofo. “Si la camioneta estaba vacía, ¿cómo es posible que entren 2 y salgan 3?”.
– “Claramente, nuestras mediciones son erróneas”, dice el físico.
– “Han debido reproducirse dentro de la camioneta”, comenta el biólogo.
– “No veo dónde está el problema”, interviene el matemático. “En cuanto entre una persona en la camioneta, esta volverá a estar vacía”.

Existe un chiste matemático basado en un chiste más o menos conocido (“¿Para qué cruzó la gallina la calle? Para llegar al otro lado”), que dice así:
– ¿Por qué la gallina cruzó la banda de Moebius?
– Para ir al otro… esto… eh…
Este chiste juega con una superficie muy peculiar que recibe el nombre de banda de Moebius, que solo tiene una cara, solo tiene un lado. De esta superficie ya hemos hablado en varias ocasiones en el Cuaderno de Cultura Científica, por ejemplo, en la entrada Guía matemática para el cómic Promethea, De menú para hoy, dos novelas gráficas negras con salsa matemática o Poesía retorcida sobre banda de Moebius.
Recordemos que una banda de Moebius es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal con dos caras, dos lados, pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara, un solo lado.
Es una sencilla construcción que puede realizarse con facilidad mientras se lee esta entrada del Cuaderno de Cultura Científica. ¿Cómo comprobar que, efectivamente, sólo tiene una cara? Si tenemos nuestra banda realizada con papel, podemos pintar con un rotulador, empezar en un punto y pintar en una dirección, y continuar pintando hasta llegar al punto en el que empezamos, entonces podemos comprobar que está pintada toda la banda, luego solo hay una cara. No ocurre lo mismo con una banda normal, ya que pintaremos la parte interior o la exterior, dependiendo de donde pongamos el rotulador, ya que tiene dos caras.
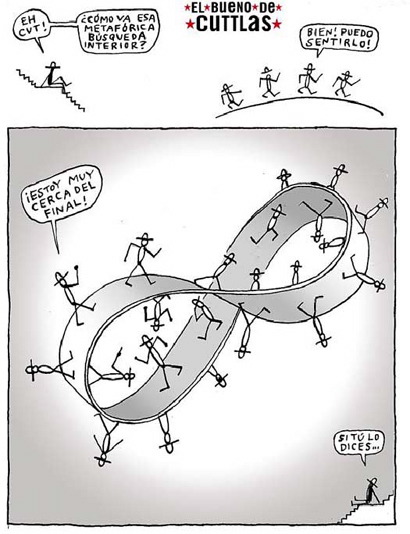
Siguiendo con la superficie de Moebius, podemos decir que en matemáticas se dice que una superficie es “orientable” cuando tiene dos caras y “no orientable” cuando tiene una cara, aunque en el lenguaje normal “orientar” tiene otro significado. Esto ha dado lugar a otro chiste.
– ¿Qué es no orientable y vive en el mar?
– Moebius Dick.
Otro juego de palabras tonto, es el siguiente.
– ¿Qué es un dilema?
– Un lema que prueba dos resultados.
Para quienes igual no lo sepan, un lema es un pequeño resultado matemático, normalmente técnico, que se demuestra antes para luego utilizarlo en la demostración de un teorema, que es un resultado matemático importante.
Seguimos con algún chiste corto más.
Las matemáticas son como el amor; una idea simple pero que a veces puede complicarse.
Incluso de bilbaínos.
Dos jóvenes de Bilbao a la salida de un examen de matemáticas:
– Oye, Patxi, ¿a ti que te ha dado en el segundo problema?
– Infinito
– ¿Solo?
Muchos resultados matemáticos consisten en demostrar algunas verdades que ocurren bajo unas determinadas hipótesis, obteniéndose así proposiciones y teoremas que podríamos expresar genéricamente como “si se dan estas condiciones, entonces esta propiedad es cierta”. Algunos chistes se ríen de esto, por ejemplo, desde la perspectiva de que no podemos asumir una hipótesis que no se ajuste al problema real que queremos resolver, como en el siguiente chiste. Aunque lo cierto es que normalmente la teoría matemática es un conocimiento que llega antes que la aplicación a un problema real concreto.
Una asociación de ganaderos quiere conseguir mejorar una raza de vacas para que den más leche, para lo cual reúnen a varios científicos y forman grupos independientes para que busquen varias soluciones, y luego adoptar la de mayor rendimiento.
Al cabo de un plazo preestablecido, empiezan a leer los resultados. Unos criadores de ganado proponen un plan de cruzamientos, y basándose en experiencias anteriores se comprometen a lograr una mejora del 3%.
El grupo de ingenieros genéticos propone introducir ciertos genes que deberían mejorar la productividad un 10%.
Un equipo de veterinarios propone unas modificaciones en los establos que harían que las vacas fuesen más felices, y producirían un 2% más de leche, que habría que sumar a las anteriores mejoras.
Otro equipo propone un cambio de dieta que mejoraría el rendimiento en un 7%, otros quieren suministrar hormonas a las vacas para subir un 8%.
Entonces aparece el equipo de los matemáticos, que dicen que son capaces de mejorar la producción en un 300%. Todo el mundo se pone muy contento, y se apresuran a leer el proyecto, que empieza diciendo: «Sea una vaca esférica …».
Un chiste en la línea de algunos de los mostrados en la entrada anterior sobre humor matemático, en relación al hecho de que los matemáticos debemos ser rigurosos y muy precisos en lo que afirmamos, es el siguiente.
Un grupo de científicas debaten sobre la cuestión “¿Qué es pi?”. Ante esta cuestión estas son sus respuestas:
La ingeniera dice “es aproximadamente 3 más 1/7”;
La física afirma “es 3,14159”;
Y la matemática, después de un buen rato pensando, concluye “pi es igual a pi”.

A continuación, vamos con uno de esos chistes en los cuales se compara la forma de trabajar, o de razonar, de diferentes ramas de la ciencia, o del conocimiento en general.
En un examen de cierta universidad para evaluar el conocimiento matemático de los estudiantes universitarios se pide demostrar que todo número impar, mayor que 2, es primo. Estas son algunas de las respuestas:
Estudiante de Matemáticas: “3 es primo, 5 es primo, 7 es primo, y por inducción, todos los números impares, mayores que 2, son primos.”
Estudiante de Físicas: “3 es primo, 5 es primo, 7 es primo, 9 no es primo –error experimental-, 11 es primo, 13 es primo, luego por inducción todos los números impares, mayores que 2, son primos.”
El estudiante de Ingeniería: “3 es primo, 5 es primo, 7 es primo, 9 es una aproximación de un primo, luego todos los impares, mayores que 2, son primos.”
Estudiante de Informática: “3 es primo, 5 es primo, 7 es primo, 7 es primo, 7 es primo, 7 es primo, …”
Estudiante de Biología: “3 es primo, 5 es primo, 7 es primo, 9 … los datos no han llegado todavía…”
Estudiante de Química: “¿Qué es un número primo?”
Estudiante de Psicología: “3 es primo, 5 es primo, 7 es primo, 9 es primo, pero trata de ocultarlo, …”
Estudiante de Ciencias Políticas: “Algunos números impares son primos … pero el objetivo es crear una sociedad más amable y agradable en la que todos los números impares sean primos”
Estudiante de Informática (de nuevo): “Creo que he encontrado un algoritmo de Knuth para la búsqueda de números primos … dadme un poco más de tiempo … he encontrado el anterior error … no, este no es … puede haber un error de compilación aquí … espera, casi lo tengo … estuve toda la noche trabajando en este programa, ya sabes … ahora si tuviese la nueva versión de este ordenador que se acaba de poner a la venta, seguro que ya lo tendría …”
Estudiante de Teología: “3 es primo, y por lo tanto todos los primos son impares. De donde se concluye la existencia de Dios, porque tal maravilla tiene que ser el resultado de una mente creadora superior; además, ¿cómo puede alguien creer en la primalidad de los números impares y negar la existencia de Dios?”
Estudiante 2 de Ciencias Políticas: “3 es primo, 7 es primo, y por tanto todos los números impares son primos de acuerdo con la doctrina del partido. Esta verdad ha sido revelada al Gran Lider y Administrador de la Paz en el Mundo. Aquellos que no estén de acuerdo son unos conspiradores contra-revolucionarios”
Estudiante de Medicina: “3 es primo, 5 es primo, 7 es primo, … al 9 y otros números como este se les aplica el mismo tratamiento hasta que se curen de su no primalidad”
El siguiente chiste está relacionado con algunas expresiones que puede utilizar el profesorado de matemáticas en clase. Por ejemplo, es muy típico que los estudiantes se quejen de que el profesor utilice la expresión “esto es trivial” en relación a un resultado matemático y no explique la razón de que se verifique, mientras que ellos no entienden por qué ocurre, luego no les parece que sea algo trivial.
Antes del chiste, podríamos recordar una interesante anécdota, relacionada con esto, que explican Claudi Alsina y Miguel de Guzmán en su libro Los matemáticos no son gente seria:
“David Hilbert marcó grandes líneas de investigación del siglo XX. Su aspecto afable, con gafas redondas, bigote y perilla blanca, constituye una de las imágenes más conocidas de la galería de matemáticos famosos. Sus anécdotas son cuantiosas. En cierta ocasión, tras una concienzuda exposición matemática, Hilbert sentenció: “lo cual es trivial”. Alguien preguntó por qué y Hilbert, tras unos segundos de reflexión, no encontró una buena respuesta. La dio al día siguiente al clamar de nuevo: “En efecto, era realmente trivial”, pero no entró en más detalles”.
Y ahora el chiste:
Qué dicen los profesores de Matemáticas, y lo que realmente quieren decir:
Claramente: No quiero pasar por todos los pasos intermedios.
Trivialmente: Si piensas que tengo que mostrarte el por qué, te equivocaste de clase.
Esto que me pregunta es obvio: Si estaba dormido cuando lo expliqué, no espere que repita la explicación.
Les doy una pista: La forma más difícil de hacerlo.
Podemos asumir que: Hay muchos casos, pero no sé cómo hacer éste.
Usando el Teorema «___»: No sé qué dice, pero sé que se resuelve por allí.
El resto es álgebra: Ésta es la parte aburrida; si no me creen, ¡háganlo!
Demostración hablada: Si la escribo, pueden encontrar los errores.
Brevemente: Ya se acaba la clase, así que escribiré y hablaré rápido (no breve).
La dejo como ejercicio: Estoy cansado.
Demostración breve: Ocupa la mitad de la hoja y cuatro veces el tiempo en entenderla.
Demostración elegante: No requiere conocimiento previo del tema y tiene menos de diez líneas de extensión.
Demostración en dos líneas: Dejaré todo de lado menos la conclusión, así no podéis poner en duda lo que no podéis ver.
Demostración formal: Yo tampoco la entiendo.
Esquema de la demostración: No pude verificar todos los detalles, así que lo dividiré en partes que no pude probar.
Fácilmente demostrable: Hasta ustedes, con sus conocimientos infinitesimales, pueden demostrarlo sin mi ayuda.
Demostración omitida: Confiad en mí, es verdad.
¿Quieren que repita la explicación?: Si ustedes la han entendido, se lo volveré a explicar hasta que no la entiendan.

Terminaremos esta segunda entrega de chistes matemáticos sobre cómo hacen el amor los matemáticos y las matemáticas en función del área de las matemáticas en el que trabajan. Por supuesto, los comentarios tienen mucho que ver con las características de esas áreas matemáticas.
– Los y las de Análisis Real lo hacen continuamente y diferencian bastante.
– Los y las de Análisis Complejo lo hacen enteramente y quedan conformes.
– Los y las de Topología Conjuntista lo hacen abiertamente, pero con tacto.
– Los y las de Combinatoria lo hacen discretamente.
– Los y las Estadísticos lo hacen aleatoriamente.
– Los y las Lógicos lo hacen de modo consistente.
– Los y las de Topología Diferencial lo hacen muuuuy suavemente.
– Los y las de Geometría Diferencial lo hacen con mucha variedad.
– Los y las de Análisis Numérico lo hacen con precisión arbitraria.
– Los y las de Teoría de la Medida lo hacen casi por doquier.
– Los y las de Teoría de Números no lo hacen y son primos.
– Los y las de Teoría de Grupos lo hacen simplemente.
– Los y las de Recursión no se deciden.
– Los y las Constructivistas lo hacen directamente.
– Los y las de Matemática Aplicada usan un ordenador para que lo haga por ellos.
– Los y las algebristas, categóricamente lo hacen.
– Los y las de Álgebra Lineal lo hacen sin discriminar.
– Los y las de Investigación Operativa maximizan las entradas y minimizan las salidas.
– Pitágoras lo hizo primero.
– Fermat lo hizo, pero no pudo probarlo.
– Gauss lo hizo mejor que nadie.
Yo que soy de geometría diferencial “lo hago con mucha variedad”. Este comentario viene del hecho de que los objetos matemáticos que se estudian en geometría diferencial son las “variedades”, que son espacios geométricos de dimensión n. O, la topología diferencial, que está muy relacionada con la geometría diferencial estudia las funciones diferenciables; pero “diferenciable” se dice también en inglés “smooth”, que es suave, por eso se dice que los de esta área lo hacen con suavidad.
Como nos recuerda Marta Macho en la entrada del Cuaderno de Cultura Científica ¿Cuántas bolas tiene el jarrón al mediodía?, el matemático británico John E. Littlewood decía:
Un buen chiste matemático es mejor, y mejor matemática, que una docena de mediocres artículos de investigación.
Bibliografía
1.- Chistes matemáticos, DivulgaMAT
2.- Andrej and Elena Cherkaev, Mathematical Jokes
3.- Rob Elliot, Si no te ríes es peor. El gran libro de los chistes, Alfaguara, 2016.
4.- Jose María Sorando, Matemáticas en tu mundo.
5.- Claudi Alsina, Miguel de Guzmán, Los matemáticos no son gente seria, Rubes, 1998.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Daniel Sanjurjo
Me ha encantado el cuidado que se ha puesto para ser inclusivo, aunque en algún caso, como en el de la matemática que fuma en pipa en la cama de la primera entrega, queda un poco raro (como raro, no imposible, es ver a una mujer fumando en pipa).