En mi anterior entrada del Cuaderno de Cultura Científica Rompecabezas matemáticos con números presentamos una serie de pasatiempos matemáticos con números relacionados con el sudoku, algunos de los cuales implicaban también las operaciones aritméticas básicas. Estos eran el sujiko, el suko, el KenKen, el Hitori y el conecta los números (o Numberlink).

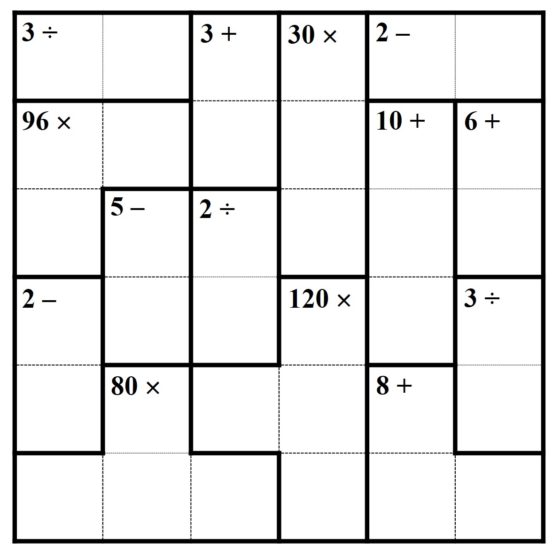
Antes de empezar con esta entrada, os dejo con uno de los rompecabezas que vimos en la anterior, por si queréis pasar un rato agradable resolviéndolo.

En esta entrada vamos a seguir presentando interesantes pasatiempos matemáticos con números. En particular, vamos a centrarnos en algunos de los rompecabezas lógicos de la editorial japonesa Nikoli, especializada en juegos y pasatiempos, de la que ya mostramos algunos en la anterior entrada, el sudoku, el Hitori y el conecta los números. Esta editorial tiene una revista de rompecabezas lógicos, que fue publicada por vez primera en agosto de 1980, llamada también Nikoli, aunque su nombre completo es Puzzle Communication Nikoli, que es una revista de pasatiempos muy importante en Japón, pero que adquirió fama mundial por el sudoku. Además, los rompecabezas de la editorial Nikoli son famosos en todo el mundo.

El primero de los juegos que vamos a presentar, denominado inshi no heya (que puede traducirse como Cajas de factorización), es una versión multiplicativa del KenKen, es decir, en todas las regiones que aparecen se considera la multiplicación. Este pasatiempo apareció por primera vez en el número 92 de la revista Puzzle Communication Nikoli.

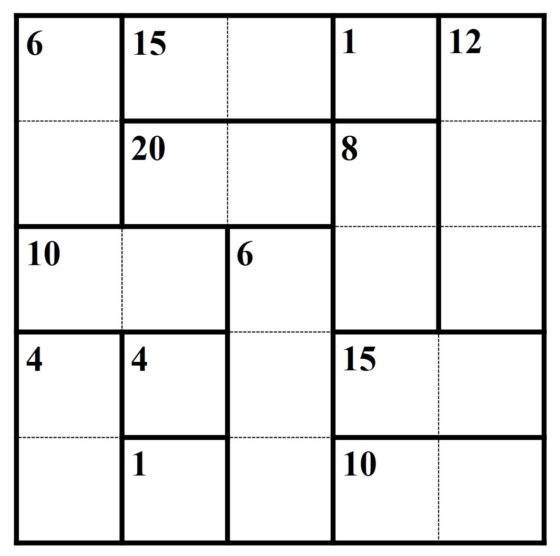
Por ejemplo, tomemos el pasatiempo inshi no heva anterior, que es el que aparece en la página web de la editorial Nikoli, entonces la solución, muy sencilla, es la que vemos a continuación.

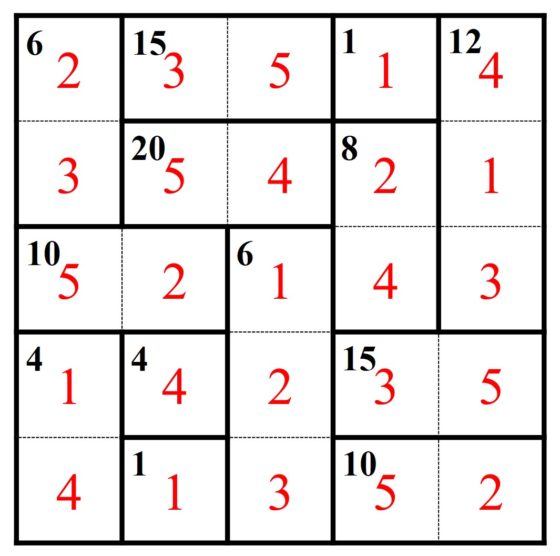
Observemos que el nombre “cajas de factorización” viene del hecho de que el número de cada región hay que factorizarlo y las entradas de las cajas son descomposiciones en producto de ese número. Por ejemplo, el 15 en una región con solo dos cajas nos dice que la factorización es 3 x 5 o el 10 es 2 x 5, mientras que en la región con un 8 y dos cajas las posibles factorizaciones son 1 x 8 y 2 x 4. Aunque con retículos más grandes la cosa se complica.

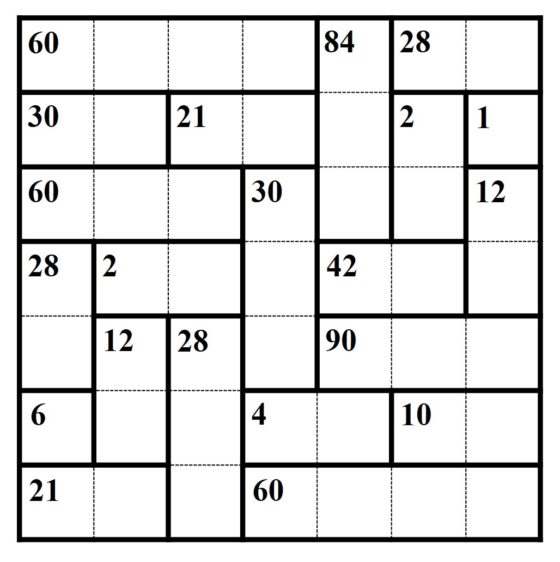
Como hemos hecho con los rompecabezas en la entrada anterior, os dejamos un inshi no heva un poco más grande para que lo resolváis. Tened en cuenta que el objetivo es disfrutar mientras lo resolvéis y sentir el placer del solitario resuelto. En algunas aplicaciones móviles con el juego KenKen se le puede pedir que solo aparezcan multiplicaciones en el rompecabezas, generando así un Inshi no heva.

El siguiente pasatiempo de la editorial Nikoli está relacionado con el rompecabezas matemático conecta los números. Es el hashiwokakero (que puede traducirse como ¡construye puentes!), que suele denominarse en inglés bridges (puentes) o chopsticks (palillos). El hashiwokakero apareció por primera vez en el número 31 (septiembre de 1990) de la revista Puzzle Communication Nikoli.

Este pasatiempo está formado por una retícula rectangular, donde algunas celdas tienen números, del 1 al 8, que normalmente están en un círculo y que reciben el nombre de islas, y el resto de celdas están vacías (como se observa en la imagen de abajo). El rompecabezas consiste en conectar las islas mediante una serie de líneas rectas (puentes) que satisfacen las siguientes condiciones:

1.- cada línea recta (puente) conecta dos islas distintas, esto es, empieza y termina en islas diferentes;

2.- cada puente no puede cruzar otro puente o pasar por encima de una isla;

3.- los puentes son horizontales o verticales, pero no diagonales;

4.- dos islas pueden estar conectadas por uno o dos puentes, pero no más;

5.- el número total de puentes que sale de cada isla es igual al número que se indica en la isla;

6.- todas las islas están conectadas en global, es decir, dadas dos islas cualesquiera se puede pasar de una a otra a través de distintos puentes e islas.

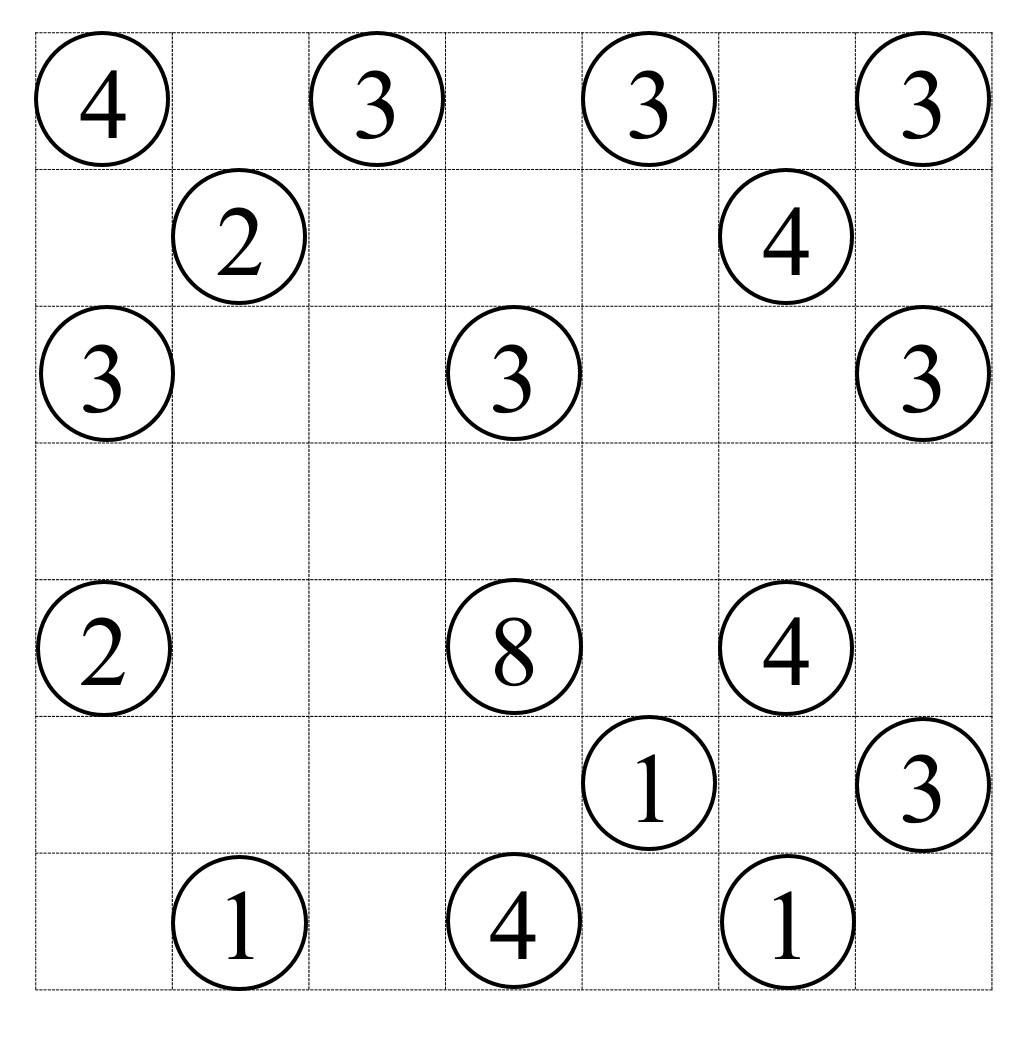
Para resolver este ejemplo podemos empezar por la isla de arriba a la izquierda que, al contener el número 4, debe tener dos puentes en horizontal (hacia la derecha) y dos puentes en vertical (hacia abajo). Por lo tanto, las islas que conectan esos puentes, que tienen ambas el número 3, deben de tener otro puente cada una. Claramente la isla con un 3 de arriba tiene que estar conectada con la siguiente isla en horizontal con un puente, ya que en vertical no hay opción. Sin embargo, la isla con un 3 que está a la izquierda, debajo del 4, puede conectarse a priori con un puente tanto en vertical (con otra isla con un 3), como en horizontal (con una isla con un 2), aunque esto último no va a ser posible porque esa isla con un 2 va a estar conectada con la isla con el 8, como vamos a comentar a continuación. Efectivamente, otra pista sencilla es la isla con un 8, que implica que tendrá dos puentes en cada una de las cuatro direcciones posibles. Y si seguimos poco a poco este razonamiento se obtiene la solución.

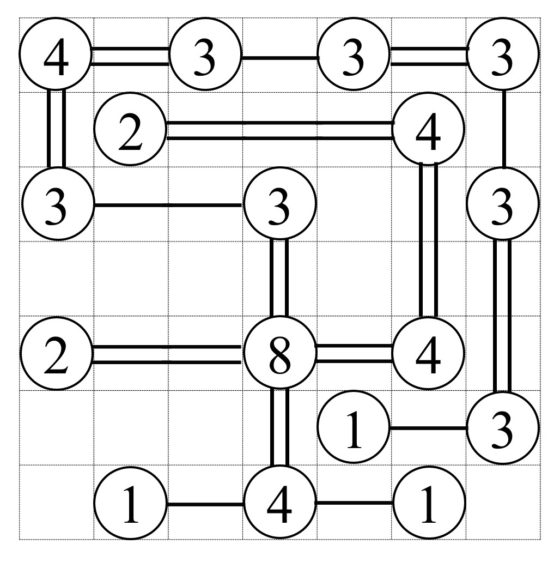
Una vez más, os dejo un pasatiempo de puentes para que lo disfrutéis, pero podéis encontrar más en algunas de las aplicaciones móviles que hay sobre rompecabezas matemáticos con números.

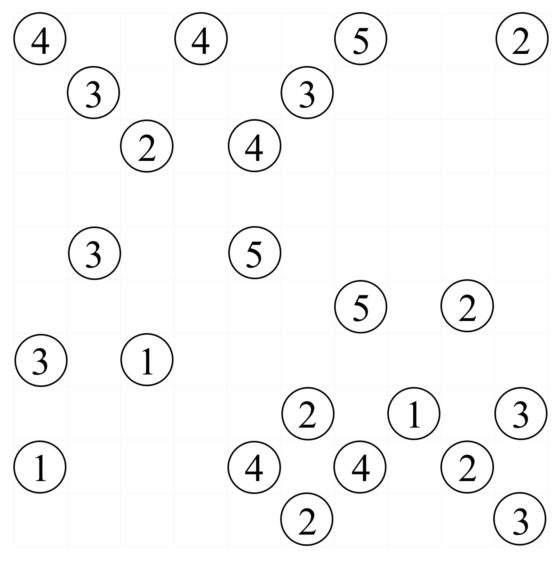
Más pasatiempos puentes, con diferentes tamaños y dificultades, los podéis encontrar en la página Puentes/Bridges.

Otro pasatiempo lógico muy interesante tanto para disfrutar resolviéndolo, como para utilizarlo en educación, como todos los que estoy presentando en estas dos entradas, es el Shikaku o divide por cajas. Por ejemplo, con el anterior pasatiempo, puentes, se trabaja tanto la parte lógica, de resolución de problemas, como la parte de factorización de números naturales, mientras que en el divide por cajas se puede trabajar además de la parte lógica, la cuestión de las áreas, pero realmente también trabaja la cuestión de la factorización, aunque más sencilla, ya que el área de un rectángulo es igual a la longitud de la base (número de cubitos de la base) por la de la altura (número de cubitos de la altura).

El rompecabezas shikaku está formado por una retícula, con números en algunas de sus celdas, de manera que hay que dividir la retícula en rectángulos de forma que cada rectángulo encierre un número y que la cantidad de celdas del rectángulo (su área) sea igual a ese número. En la imagen de abajo mostramos un ejemplo.

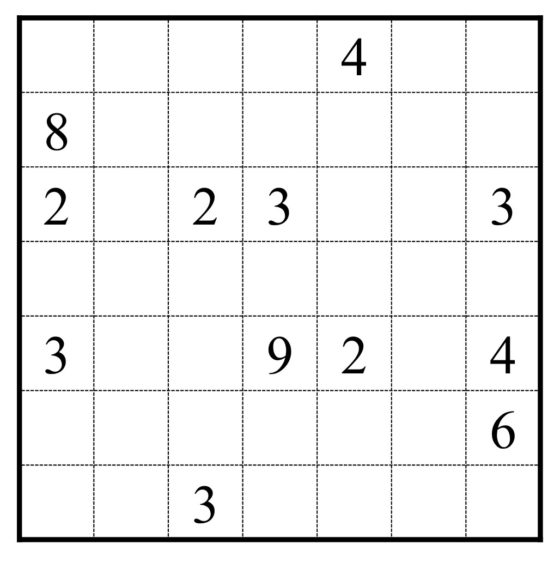
Veamos cómo resolver este sencillo ejemplo, que nos da una idea de qué tipo de razonamiento lógico hay que realizar. Por ejemplo, el 8 que está arriba a la izquierda debe de encerrar un rectángulo con 8 casillas, pero no hay más opción que el rectángulo 4 x 2 apoyado en la esquina superior izquierda, o el nueve que aparece tiene que corresponderse con un cuadrado de lado 3 casillas, pero solo hay un cuadrado posible con 9 casillas que contenga el número 9. Y poco a poco vamos obteniendo todos los rectángulos, como se ve en la siguiente imagen.

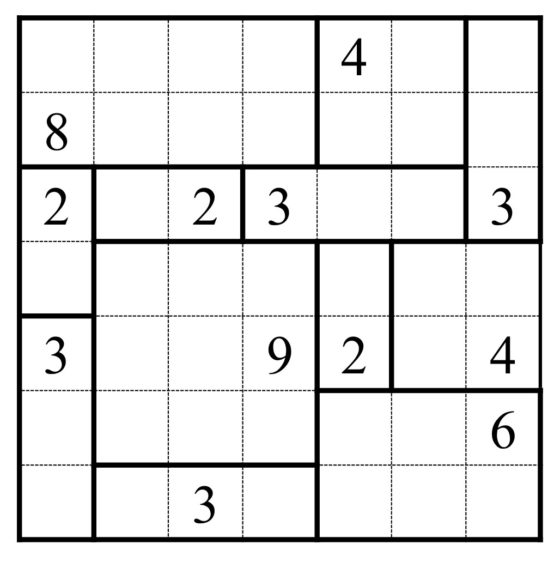
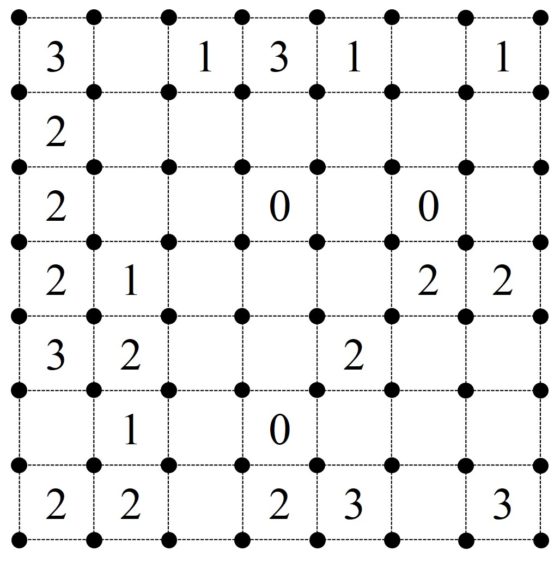
Os dejo un nuevo rompecabezas Shikaku, extraído de la página Shikaku.

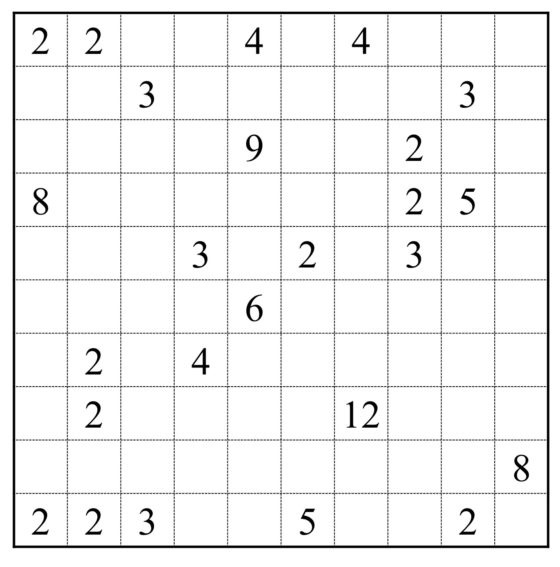
Otro de los rompecabezas lógicos de la editorial Nikoli es el Slitherlink, también conocido como Loop, es decir, lazo. Una vez más el pasatiempo consiste en una retícula en la que están marcados todos los vértices, como se ve en el siguiente ejemplo, y aparecen números en algunas casillas. Las reglas de este solitario son:

1.- el objetivo es construir un camino continuo y cerrado, un lazo, conectando los vértices adyacentes con líneas verticales y horizontales;

2.- los números indican la cantidad de segmentos pintados que hay alrededor del mismo y cuando no hay números puede ser cualquier cantidad, desde ninguna a cuatro líneas;

3.- el lazo no contiene intersecciones, ni ramificaciones.

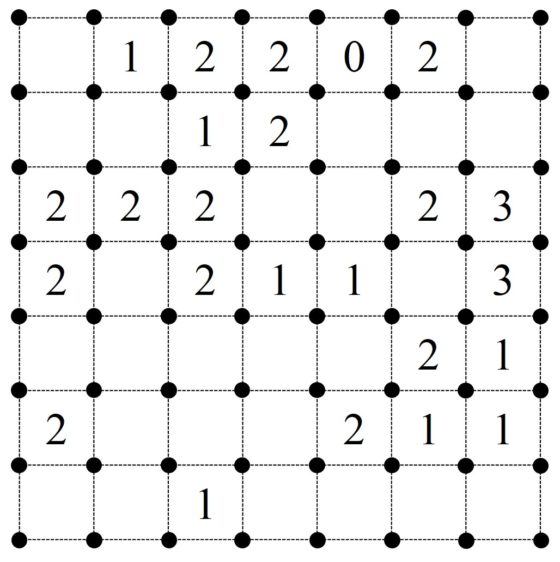
El punto de inicio nos lo da la casilla con un 0, ya que no solo no está ninguna de las cuatro líneas alrededor del mismo, sino que tampoco están la línea de encima del 2 de la izquierda, que al continuarla nos daría lugar a una línea alrededor del 0, ni la línea de encima del 2 de la derecha. Por lo tanto, las dos líneas alrededor de esos dos 2s están claras, y las pintamos. A partir de ahí se puede seguir un poco más de una forma lógica y sencilla, teniendo en cuenta que el lazo es un camino continuo. Por ejemplo, un punto intermedio al que se llega fácilmente es el que mostramos en la siguiente imagen.

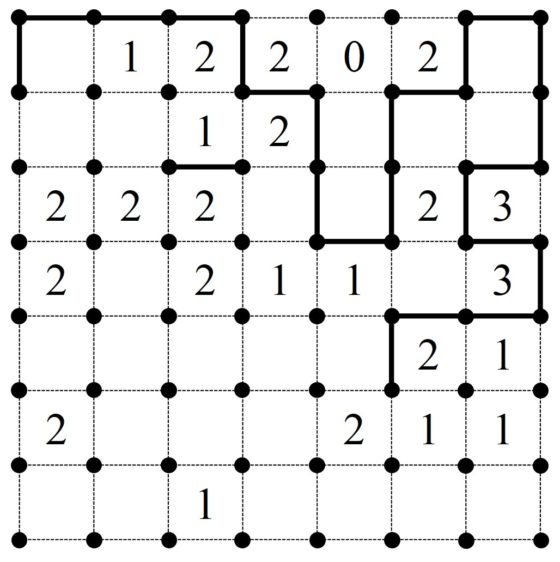
En este punto, podríamos razonar cómo seguir la línea vertical que está alrededor del 2, abajo a la derecha. No se puede seguir con una línea horizontal hacia la derecha ya que en ese caso el 2 de arriba tendría tres líneas a su alrededor y no se puede continuar con una línea vertical hacia abajo porque ese movimiento dejaría al 1 de la derecha sin líneas o a la línea encerrada en esa esquina sin poder continuarse, luego se continúa con una línea horizontal hacia la izquierda. Esa línea se debe de seguir hacia delante, horizontalmente, para que el 2 no tenga tres líneas a su alrededor, en esa casilla blanca tendremos tres segmentos pintamos y volveremos hacia la derecha para poder pasar por las dos casillas con un 1 en su interior.

Además, el 1 de la casilla central también nos da información para seguir. Para empezar la única línea que puede estar pintada a su alrededor es la vertical de la izquierda y podemos seguir un poco más. En este punto estaremos como se muestra en la siguiente imagen.

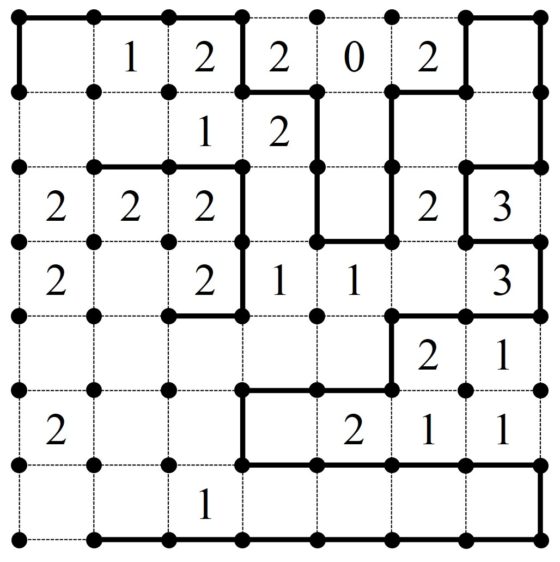
Y con un poco más de lógica, teniendo en cuenta las reglas del juego se concluye la solución.

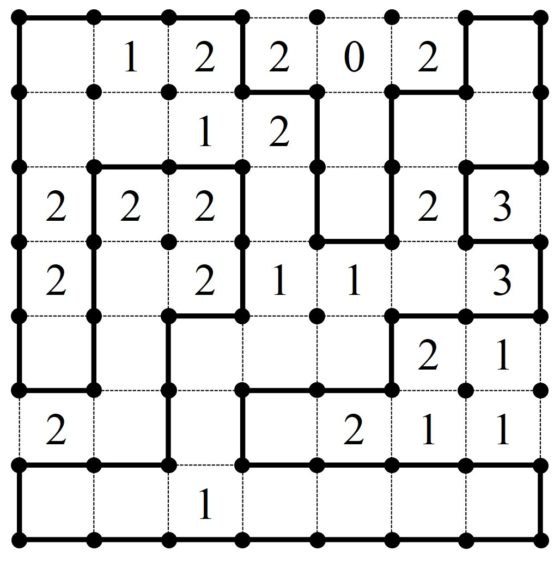
A continuación, os dejo un pasatiempo lazo más complicado que el anterior, que he cogido de la colección de rompecabezas de Simon Tatham.

Otro juego solitario de tipo lógico muy interesante, que fue desarrollado por la editorial Nikoli en 2001, es el akari, que en inglés se conoce como Light up, y en castellano, iluminar.

El pasatiempo iluminar consiste en una retícula rectangular con algunas celdas negras y el resto blancas; además, en algunas de las celdas negras hay números. El objetivo del solitario es colocar bombillas (circunferencias) en algunas de las casillas blancas respetando las siguientes reglas:

1.- el número de las casillas negras indica cuantas bombillas están en contacto, horizontal y verticalmente, con esa casilla negra;

2.- cada bombilla ilumina, en horizontal y vertical, todas las casillas que hay desde la bombilla hasta una casilla negra o el límite de la retícula;

3.- todas las casillas blancas tienen que estar iluminadas, pero ninguna bombilla puede iluminar a otra bombilla.

A continuación, mostramos un sencillo ejemplo, extraído de la página Light up, que nos permita entender mejor las reglas de este juego de ingenio.

Veamos cómo podemos resolverlo. Para empezar el número 3 de la casilla negra que está a la derecha, hacia abajo, nos dice que tres bombillas están en contacto, horizontal y verticalmente, con ella, pero solo hay tres opciones, luego colocamos esas tres bombillas. En la siguiente imagen mostramos las tres bombillas y las casillas blancas iluminadas por ellas.

Como las bombillas no pueden iluminarse unas a otras no podemos colocar bombillas en las casillas iluminadas por las anteriores bombillas, por lo tanto, como las dos casillas negras con el número 2 solo tienen dos casillas blancas adyacentes en las que se pueden colocar las bombillas, entonces está claro que debemos colocarlas en esas casillas. La situación entonces, teniendo en cuenta las casillas blancas que iluminan esas nuevas bombillas, es la siguiente.

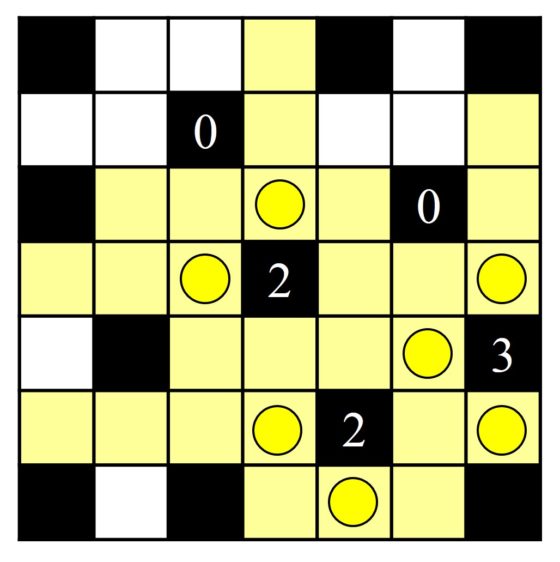
Ahora ya solo nos queda concluir el pasatiempo teniendo en cuenta además que alrededor de las casillas negras con un 0 no puede haber ninguna bombilla, en horizontal y vertical. La solución por lo tanto es la que mostramos.

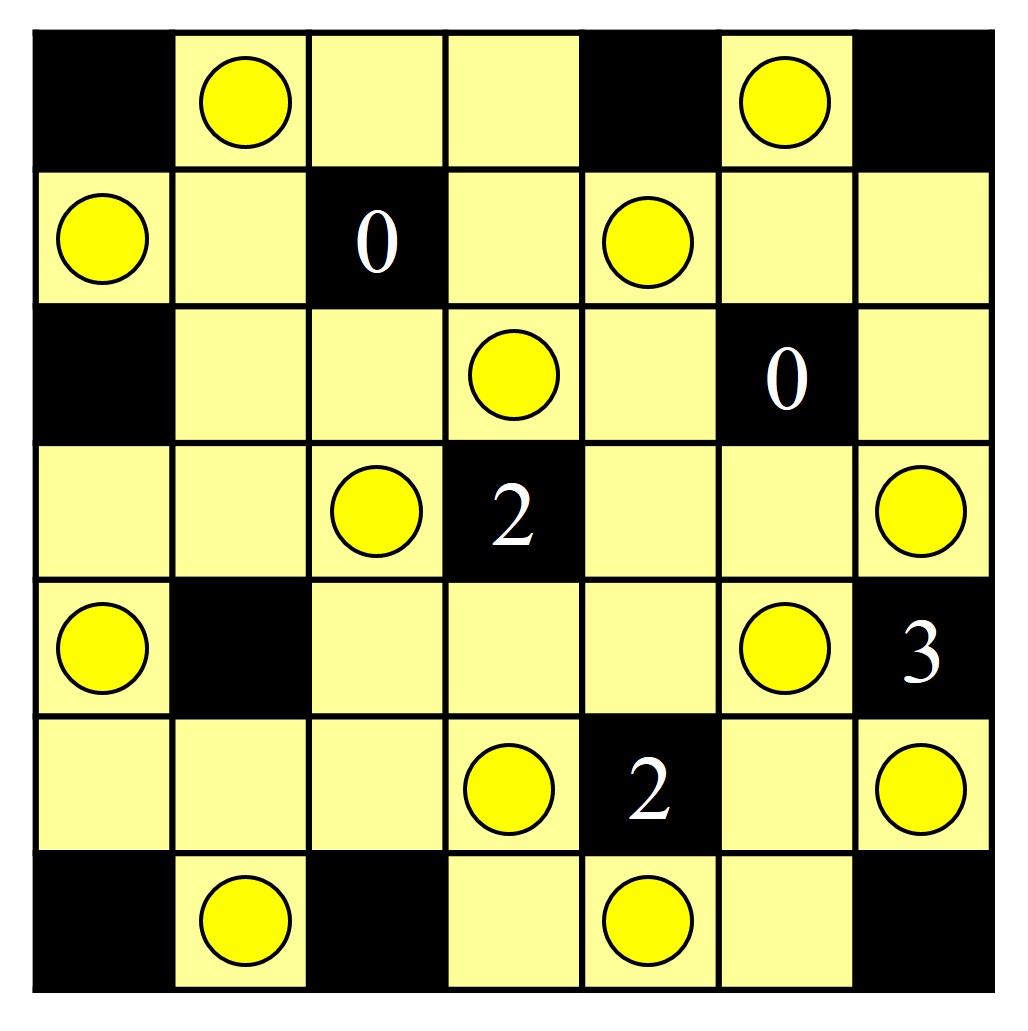
Y una propuesta para que os divirtáis, también de la página Light up.

Parafraseando a un matemático inglés que ha recibido el premio Abel de matemáticas por la demostración del teorema de Fermat, “creo que lo dejaré aquí”, aunque hay más rompecabezas matemáticos con números muy interesantes de la editorial Nikoli.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica