En enero de 2014 se publicó en el periódico New York Times, en su columna de juegos y crucigramas Wordplay, un problema de ingenio bajo el título El problema de la princesa, que nosotros hemos reescrito para esta entrada del Cuaderno de Cultura Científica como El problema de la matemática excéntrica.

El problema de la matemática excéntrica: Érase una vez una matemática que vivía en un enorme castillo. El ala este del edificio, en la que ella hacía su vida, disponía de un largo pasillo con diecisiete habitaciones, cada una de las cuales tenía una puerta que daba al pasillo, para entrar y salir de la misma, así como una puerta conectando con cada habitación contigua. La matemática era un poco excéntrica y no le gustaba dormir dos noches en la misma habitación. Por este motivo, cada noche cambiaba y dormía en una habitación adyacente a la que había dormido la noche anterior, elegida al azar.

La habitante del castillo era una prestigiosa matemática con la que muchas personas querían investigar. Por este motivo, cuando alguien le proponía colaborar con ella, invitaba a esa persona a pasar treinta días en su castillo, en el ala oeste para invitados, para que pasara dos pruebas. La primera era que durante esos treinta días demostrase tener los conocimientos necesarios para investigar con ella y la otra era un entretenido reto. La excéntrica matemática, tras explicar sus manías para dormir, proponía a su invitada que cada mañana llamara a una de las diecisiete puertas, si ella abría la puerta, porque había pasado la noche en esa habitación, el reto estaría superado, si no podría intentarlo al día siguiente. Si tú fueses la persona invitada al castillo, ¿podrías desarrollar una estrategia para encontrar a la matemática antes de que pasen los treinta días?

Este problema había aparecido, en 2010, en el hilo math puzzles for dinner (rompecabezas matemáticos para la cena) de Christian Blatter para MathOverflow, que en la propia página se describen como “una página web de preguntas y respuestas para matemáticos profesionales”.

Por otra parte, el matemático ruso Alexander Shapovalov en su página web [ashap.info/], en el apartado dedicado a “problemas para divertirse y para competiciones matemáticas” afirma que el problema fue presentado por el matemático ruso V. Shorin y él mismo en la competición internacional Tournaments of Towns, que es una especie de olimpiada internacional para educación primaria que se originó en Rusia, en la edición de 1999.

Dos años después de la publicación del problema de la búsqueda de la princesa en el hilo math puzzles for dinner (rompecabezas matemáticos para la cena) de MathOverflow, los matemáticos británicos John R. Britnell y Mark Wildon hicieron público su artículo Finding a princess in a palace: A pursuit-evasion problem (Buscando una princesa en un palacio: un problema de persecución-evasión) en el analizaban matemáticamente el problema de la princesa sobre un grafo, donde las habitaciones son los vértices del grafo y las aristas son las puertas que comunican dos habitaciones.

Recordemos que un grafo está formado simplemente por puntos –llamados vértices del grafo- y líneas que unen algunos de esos puntos –llamadas aristas del grafo- (véase, por ejemplo, El problema de los tres caballeros y los tres criados, El grafo de Marion (Gray) o El juego de Sim, entre otros), y que es una estructura matemática muy sencilla, pero a la vez muy versátil.

Como ya se indica en el título del artículo de Britnell y Wildon, este pasatiempo pertenece a la familia de problemas de tipo persecución-evasión (como el “juego de policías y ladrones”), que son aquellos en los cuales un grupo –en este caso quien intenta resolver el rompecabezas– intenta localizar a los miembros de otro grupo –en este caso la excéntrica matemática– en un entorno cerrado –las diecisiete habitaciones comunicadas de forma lineal–.

El estudio matemático de los problemas persecución-evasión sobre grafos se remonta a la década de 1970. Por ejemplo, en el artículo Pursuit-evasion in a graph se plantea ya la cuestión general: “Supongamos que una persona está perdida y vagando por una oscura cueva. Un grupo de rescate que conoce la cueva será enviado para buscarle. ¿Cuál es el mínimo número de personas en el grupo de rescate que se necesita para encontrarle independientemente de cómo se comporte?”.

Y seguía explicando: “Existen muchas formulaciones matemáticas, no equivalentes, de este problema, dependiendo de la naturaleza de la cueva y los posibles comportamientos de la persona perdida y de las personas del grupo de rescate. […] Un ejemplo es una cueva circular, que requiere un mínimo de dos personas en el grupo de recate: la persona perdida podría moverse siempre en la parte opuesta a una única persona de rescate”.

Pero regresemos al problema de la matemática excéntrica y planteemos cómo resolverlo. Lo primero que hay que hacer siempre es leer bien el rompecabezas e intentar entender todos los elementos que aparecen en el mismo. Además, en problemas como este, en el cual aparecen diecisiete habitaciones conectadas en línea, lo mejor es simplificar el problema, para comprender bien en qué consiste y analizar la solución en una situación sencilla, para luego ir complicándola hasta tener la idea de la solución del problema original. Por este motivo, imaginemos que en el pasillo del castillo solo hubiese tres habitaciones en línea, como en la siguiente imagen.

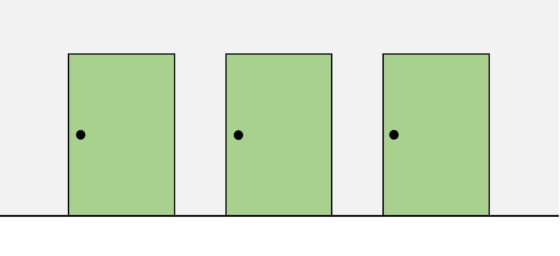
Antes de abrir ninguna puerta, la matemática puede estar en cualquier habitación, por este motivo hemos pintado de verde las puertas. ¿Qué puerta deberíamos abrir el primer día? La mejor opción es la puerta que está en el medio.

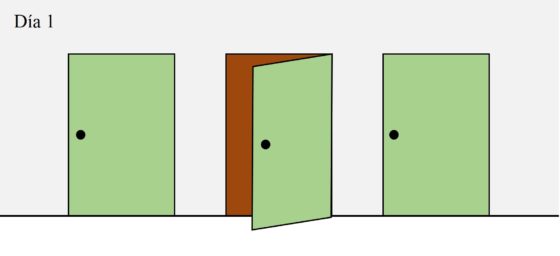
Si la matemática está en esa habitación, la hemos encontrado y se terminó. Pero si no está, entonces estará en cualquiera de las dos habitaciones, las de los extremos. Teniendo en cuenta la costumbre de la matemática de dormir cada noche en una habitación distinta, pero adyacente, la siguiente noche necesariamente dormirá en la habitación de en medio. Por lo tanto, si el segundo día abrimos la puerta de esa habitación la habremos encontrado.

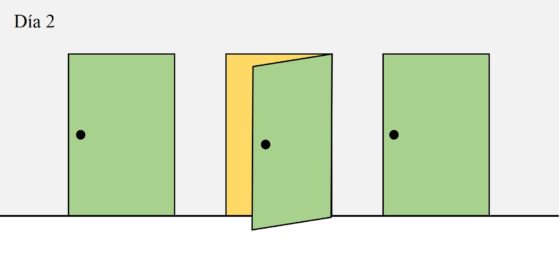
En conclusión, si seguimos esta estrategia como mucho tardaremos dos días en encontrarla, resolviendo en ese plazo el reto propuesto.

¿Qué habría pasado si el primer día hubiésemos abierto una de las puertas de los extremos? Si al abrir esa puerta la habitación estuviese vacía, al día siguiente la matemática podría estar de nuevo detrás de cualquiera de las tres puertas y sería otra vez una cuestión de suerte. Abrir alguna de las puertas de los extremos no aporta ninguna certeza sobre dónde puede estar, o no estar, la matemática.

Compliquemos un poco más el problema y consideremos ahora que en el pasillo hay cuatro puertas. ¿Cuál debe ser la estrategia para encontrar a la matemática en la menor cantidad de días posibles? Ahora hemos añadido un número encima de cada puerta para identificar mejor cada una de las habitaciones.

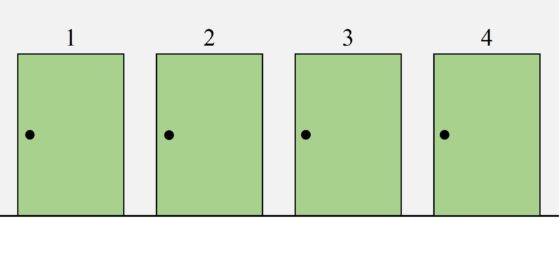
¿Qué ocurriría si empezamos abriendo, el primer día, la puerta número 2, siguiendo la misma idea del anterior caso?

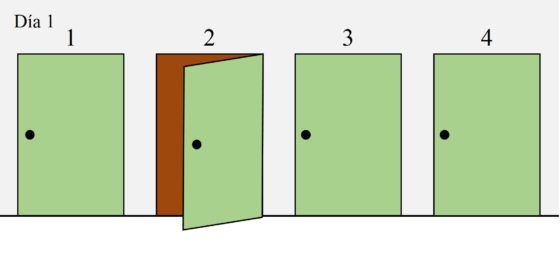
Si al abrir la puerta número 2 la matemática está ahí, entonces la hemos encontrado, aunque haya sido con un poco de suerte, ya que teníamos una probabilidad de 1 entre 4 de acertar. Pero si no hay nadie en esa habitación, al menos tenemos una pista para el siguiente día. No podrá estar en la habitación 1, puesto que para eso tendría que haber estado en la habitación 2 el día anterior, por su manía de trasladarse solo a habitaciones adyacentes.

La apertura de puertas debe estar pensada para obtener algunas certezas para el siguiente día e ir eliminando opciones. Por este motivo, el segundo día abriríamos la puerta 3.

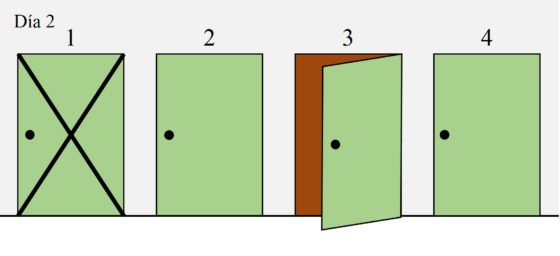
La probabilidad de que la matemática esté tras la puerta número 3 el segundo día es de un tercio. Pero si no está en esa habitación preguntémonos qué conclusiones podemos extraer para el siguiente día. Como la habitación 2 tiene a las habitaciones 1 y 3 como adyacentes y no estaba en esas habitaciones el segundo día, entonces el tercer día no va a poder estar en la habitación 2. Lo mismo pasa con la habitación 4, que tiene a la habitación 3 como única adyacente. Por lo tanto, solo tenemos dos opciones posibles para el tercer día, habitaciones 1 y 3.

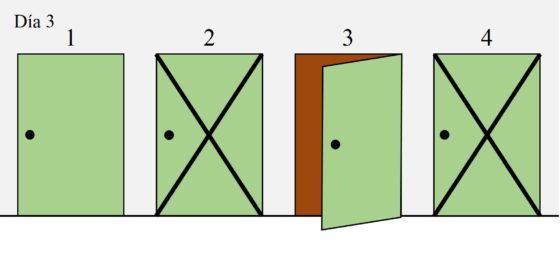
Por lo tanto, vamos a abrir la puerta 3. Si la científica no está detrás de esa puerta, al día siguiente solo podría estar en la habitación 2 y al cuarto día, como mucho, la habríamos encontrado.

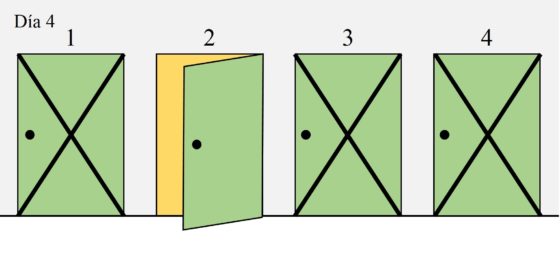
Por otra parte, si el primer día empezamos abriendo las puertas 1 o 4 no obtendremos ninguna información para el día siguiente, por lo tanto, no son opciones buenas para empezar a buscar a la matemática excéntrica.

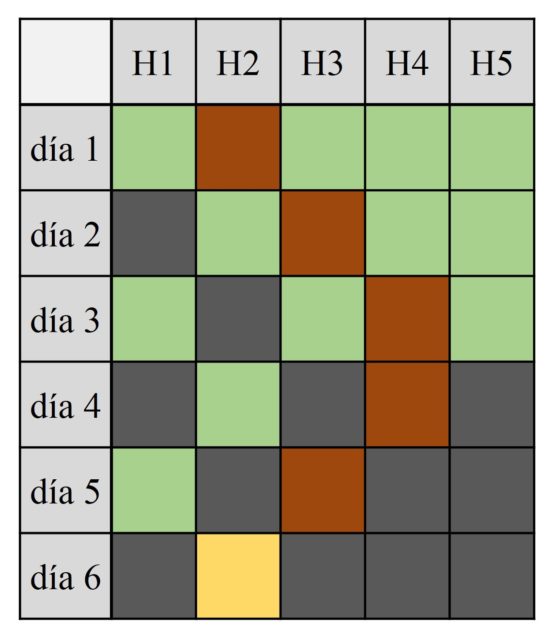
Podemos resumir nuestra estrategia para cuatro habitaciones, con las diferentes opciones, en la siguiente tabla. Cada columna es una habitación y cada fila un día. Además, las celdas verdes son las habitaciones en las que puede estar la matemática, las celdas marrones las que abrimos cada día, las celdas grises en las que no puede estar y la celda amarilla en la que va a estar finalmente, si no la hemos encontrado antes.

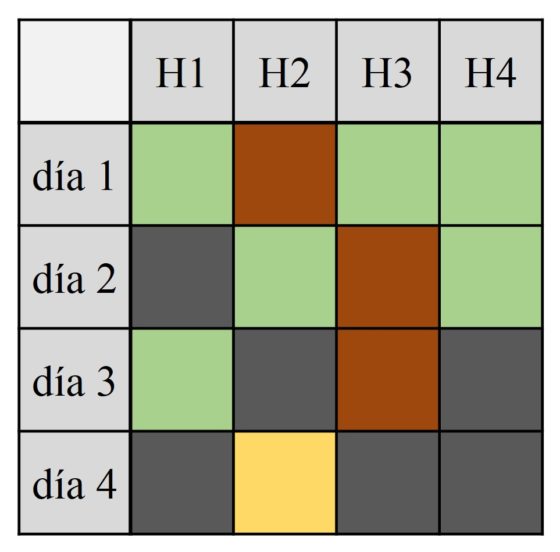
Por lo tanto, la secuencia de apertura de puertas [2, 3, 3, 2] es una estrategia ganadora para encontrar a la matemática. Así mismo, el razonamiento que hemos hecho nos dice que no podemos estar seguros de encontrarla en menos movimientos.

Si ahora analizamos el problema de la matemática excéntrica con cinco habitaciones, la estrategia ganadora es [2, 3, 4, 4, 3, 2] como queda explicada en la siguiente tabla. Es decir, se necesitan un mínimo de seis días para encontrar, con toda seguridad, a la persona buscada.

Si ahora volvemos al problema original, con diecisiete habitaciones, se podría dibujar una tabla similar a las anteriores y obtener que la estrategia ganadora es [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2]. Se necesitan, como mucho, treinta días para encontrar a la dueña del castillo.

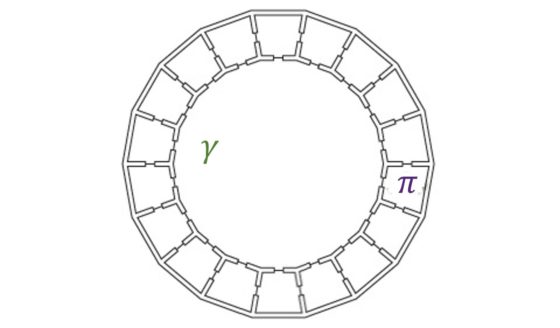
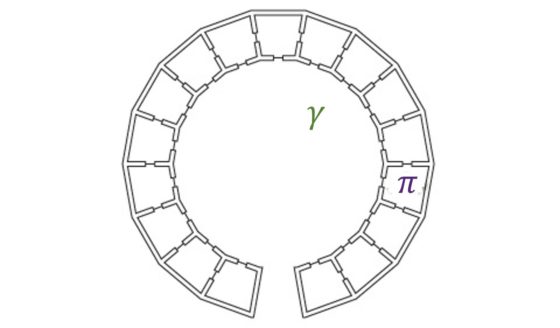
Si observamos la imagen que acompañaba al pasatiempo matemático en el New York Times nos podemos plantear claramente qué ocurriría si tuviésemos habitaciones, por ejemplo, dieciocho, distribuidas en un pasillo circular, como en la anterior imagen. Ahora no existe ninguna estrategia ganadora que nos asegure que podemos encontrar a la matemática. Podría pasar que siempre abriéramos una puerta en la que no está, incluso la que está en la posición diametralmente opuesta. En este caso todo se reduce al azar.

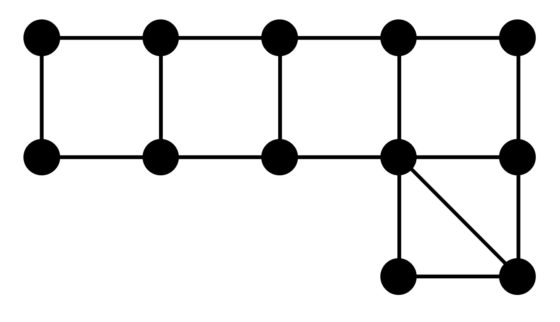
De hecho, nos podemos plantear si existen estrategias ganadoras dependiendo de la forma en la que están conectadas las habitaciones (matemáticamente, para diferentes grafos). Claramente, por lo comentado en el ejemplo circular, cualquier distribución/grafo que tenga ciclos, partes circulares, no va a tener estrategia ganadora. En el artículo Finding a princess in a palace: A pursuit-evasion problem (Buscando una princesa en un palacio: un problema de persecución-evasión) se mostraba el grafo más sencillo, sin partes circulares, en la cual la matemática podría no ser encontrada. Es la que mostramos en la siguiente imagen.

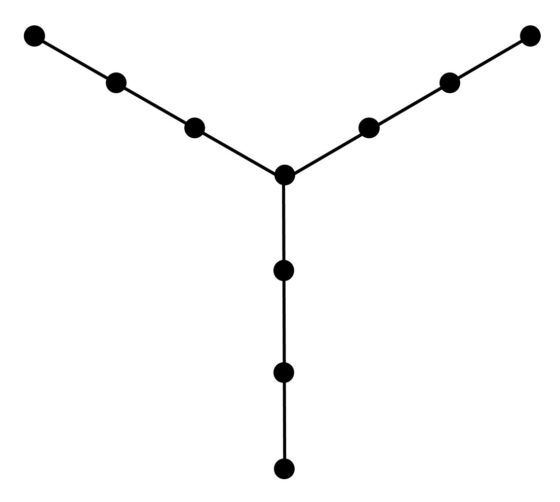
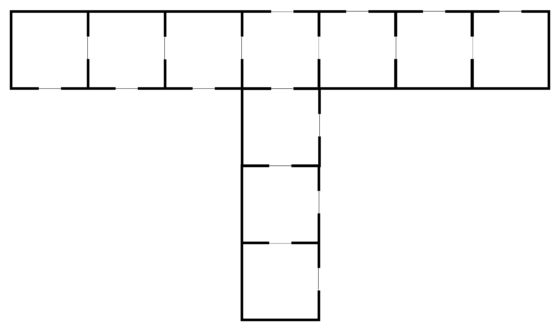
Como cada vértice se corresponde con una habitación y cada arista a una puerta entre habitaciones, la distribución de habitaciones relacionada con el anterior grafo es la que aparece en la siguiente imagen.

Un juego clásico de la familia de problemas de tipo persecución-evasión es el juego de policías y ladrones, del que ya hablaremos en alguna otra entrada del Cuaderno de Cultura Científica. Para abrir boca, vamos a terminar esta entrada con una versión sencilla de este juego.

Reglas del juego policías y ladrones:

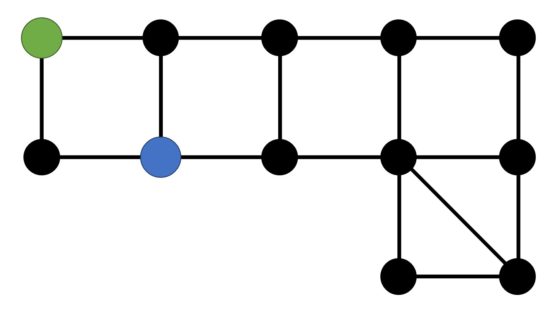
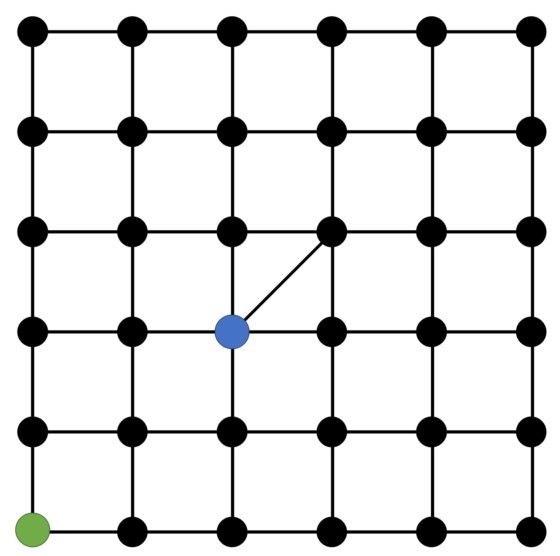
El tablero del juego consta de doce posiciones posibles –puntos negros– conectadas con líneas, como aparece en la imagen.

Es un juego para dos jugadores, el policía y el ladrón, cada uno con su ficha. La posición inicial de las fichas del policía (azul) y del ladrón (verde) es la que aparece en la imagen.

El objetivo del juego es doble. El policía debe intentar atrapar al ladrón, es decir, colocar su ficha en la posición en la que esté la ficha del ladrón; y el ladrón debe intentar no dejarse atrapar. Las reglas son las siguientes:

i) cada jugador, policía y ladrón, mueve su ficha obligatoriamente de una posición a otra que esté conectada con una línea;

ii) cada jugador, de forma alternada, realiza un solo movimiento por turno;

iii) empieza moviendo el policía.

El juego termina cuando el policía atrapa al ladrón o cuando desiste de hacerlo.

En el libro Matemáticas para divertirse de Martin Gardner se presenta este juego, pero con otro tablero y con un zorro y un ganso en lugar de un policía y un ladrón. El tablero es el de la siguiente imagen, con las posiciones iniciales que se muestran.

Bibliografía

1.- John R. Britnell, Mark Wildon, Finding a princess in a palace: A pursuit-evasion problem, The Electronic Journal of Combinatorics 20 (1), 2013.

2.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

3.- T. D. Parsons, Pursuit-evasion in a graph, en Theory and Applications in Graphs, Springer-Verlag, 1978, pp. 426-441.

4.- F.V. Fomin, D.M. Thilikos, An annotated bibliography on guaranteed graph searching, Theoret. Comput. Sci. 399, pp. 236-245, 2008.

5.- Tatjana V. Abramovskaya, Fedor V. Fomin, Petr A. Golovach, Michał Pilipczuk, How to hunt an invisible rabbit on a graph, European Journal of Combinatorics 52, pp. 12-26, 2016.

6.- Mohammed Ammar, Is it possible to catch the thief? , del canal de youtube Logically yours.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica