Pablo Rodríguez Sánchez
Este no es mi primer artículo de divulgación. De hecho, si las cuentas no me fallan, es mi centésimo décimo quinto. Sin embargo, es el primer artículo de divulgación en el que hablo de mi propia investigación. Para alguien con una verborrea como la mía, semejante timidez y silencio respecto a mi propio trabajo son, cuanto menos, llamativos. Sospechosos incluso. Pero todo tiene una explicación: he pasado tanto tiempo embarrado ocho horas diarias con estos problemas que para cuando les puse las guinda y fueron publicados… ya hacía meses que habían dejado de divertirme.
Un artículo científico, peor aún si trata sobre matemáticas, se acerca mucho a la antítesis de la diversión. Especialmente para el que lo lee. Hace falta mucha habilidad para hacerlo entretenido, habilidad que yo no tengo. Sin embargo, escribir un artículo científico es una actividad humana llena de altibajos, frustraciones y curiosidades. Ingredientes estos no muy diferentes de los que uno puede encontrar en algunas novelas, películas e incluso chistes.
Permítanme que les cuente aquí la intrahistoria de mi artículo, pues esta, al contrario que el frío y técnico contenido, es completamente inédita.

El arte, las matemáticas y yo
Lo reconozco. Hubo un tiempo en el que cada vez que escuchaba juntas las palabras “arte” y “matemáticas” me ponía en guardia. Será que he visto demasiadas películas infumables, demasiadas obras de arte pretenciosas (y a menudo feas), o simplemente que estoy hecho un gruñón.
Digo «hubo un tiempo», en pasado, porque actualmente veo la combinación “arte y matemáticas” con ojos más benévolos. Esto se debe a que este dueto me ha proporcionado muchos buenos momentos en los últimos años. Algunos ejemplos son mi colaboración con el videoartista Johan Rijpma, mis charlas en Naukas, o la historia que hoy les traigo.
Como pez fuera del agua
Permítanme que les ponga en antecedentes. En 2015 comencé un doctorado en matemáticas aplicadas en un departamento de ecología. Esto significaba, entre otras cosas, que tenía que escribir artículos sobre matemáticas que fuesen interesantes para la comunidad ecológica.
La mayoría de ecólogos se pueden clasificar en tres categorías: ecólogos de campo, ecólogos de laboratorio y ecólogos computacionales. O si lo prefieren, ecólogos de bota, de bata y de byte. Los ecólogos suelen tener formación en biología, y cualquier suposición sobre su interés por las matemáticas está abocada al fracaso: este puede ir desde casi nulo a altísimo.
Todo esto plantea una dificultad enorme desde el punto de vista de la comunicación: ¿cómo abordar los problemas matemáticos de la ecología sin perder ni aburrir a nadie? En este otro artículo, publicado en esta misma casa, ofrezco algunos consejos generales. Pero permítanme ir de lo general a lo particular, y explicar cómo el arte me echó una mano en cierta ocasión.
La estabilidad como paisaje
Uno de estos problemas de comunicación interdisciplinar es el siguiente: en ecología aparecen de forma bastante natural conceptos procedentes de la teoría de sistemas dinámicos. Hablo de conceptos como ecuación dinámica, clasificación de equilibrios o teoría de bifurcaciones.
Para los matemáticos, los sistemas dinámicos no son nada más (ni nada menos) que unas reglas, normalmente en forma de ecuaciones, que dictan cómo debe moverse un punto. Ese punto puede representar muchas cosas. Una temperatura a lo largo del año, los ahorros presentes en una cuenta bancaria, la cantidad de peces que viven en un lago, etcétera. En definitiva, cualquier cosa que pueda medirse y cambie en el tiempo. Si las reglas están bien fundadas, podemos usarlas nada menos que para predecir la evolución futura de la variable bajo estudio. Un buen ejemplo son los problemas de mecánica, donde conociendo las fuerzas que actúan sobre un objeto podemos calcular cómo se moverá este.
Estos puntos, según cual sea el problema, pueden moverse por una línea recta, por un plano, por el espacio tridimensional, o por inimaginables hiperespacios de cuatro o más dimensiones. Todo depende del número de variables que estemos estudiando (una temperatura, las poblaciones de dos especies de peces, las tres dimensiones de un objeto en movimiento, etc).
Una manera muy habitual de introducir estos conceptos, que ha demostrado su eficacia en innumerables ocasiones, es usando algo que la comunidad ecológica llama stability landscape o ball-in-a-cup diagram (lo que podríamos traducir libremente como «paisaje de estabilidad» o “diagrama de la bolita en el vaso»; no me miren así, yo no les he puesto esos nombres). La idea consiste en construir una curva sobre la cual una bolita se deja rodar, de modo que la forma de la curva, la forma del «paisaje», nos indica cómo ha de moverse1. Al fin y al cabo la teoría de sistemas dinámicos, recordemos, trata de describir cómo se mueve un punto… y dejar rodar una bolita es, en principio, una manera como otra cualquiera de mover un punto de acá para allá. La idea es muy gráfica y explota nuestra natural intuición respecto al movimiento. Ahí radica su fuerza.
Si, además, permitimos que la forma de los «paisajes» cambie en respuesta a condiciones externas (como temperatura, pH, salinidad, …), estas metáforas gráficas pueden usarse para ilustrar conceptos bastante avanzados, como los de estabilidad, bifurcación, o histéresis (ver ejemplo en la figura, y más aquí).
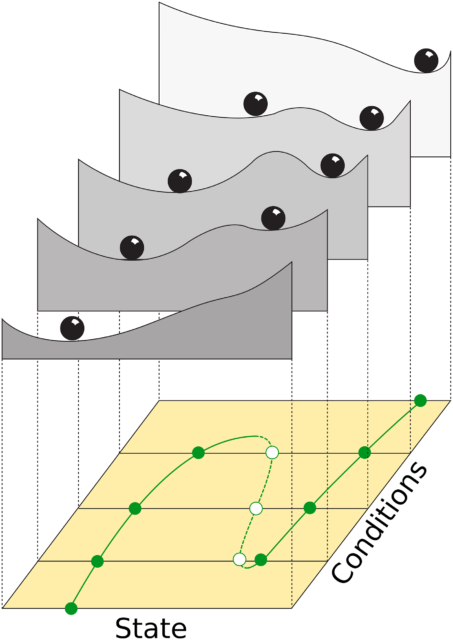
La parte superior de la figura muestra el «paisaje» correspondiente a un sistema dinámico para 5 valores diferentes de las condiciones externas. La parte de abajo muestra, en verde, el diagrama de bifurcación correspondiente, donde los puntos sólidos representan equilibrios estables (correspondientes al fondo de un «valle») y los vacíos equilibrios inestables (correspondientes a una «cresta»). Obsérvese como no sólo la posición, sino también el número de puntos de equilibrio varía con las condiciones externas. Una de las consecuencias de esto es que, para ciertas condiciones externas, el comportamiento del sistema puede cambiar de manera drástica.
Es posible que el lector se haya dado cuenta de que estos «paisajes» se parecen mucho al concepto de potencial en mecánica clásica. De hecho, son casi lo mismo2.
Pedir peras al olmo
Utilizar aproximaciones y analogías gráficas tiene sus ventajas y sus peligros. Algunos, incluso, son ventaja y peligro a la vez. El hecho de que las cosas parezcan más sencillas de lo que realmente son es una de estas ventajas peligrosas.
Muchos biólogos trabajan con sistemas dinámicos de dos variables. Por ejemplo, una coordenada x describiendo una especie de pez, y la coordenada y describiendo a otra. A menudo los peces x se comen a los peces y. ¿Y si usamos estos “paisajes de estabilidad” en modelos con dos (o más) variables? Si una bola rodando sobre curva nos sirve representar la dinámica de una variable, una bola rodando sobre una superficie nos servirá para representar la dinámica de dos variables, ¿no?
En principio no parece mala idea, pero cualquiera que lo intente no tardará en encontrarse en un callejón sin salida. Lo que funciona de maravilla para una variable se convierte en una pesadilla cuando se intenta aplicar a dos o más. En el mejor de los casos, el «paisaje» puede calcularse para algún subcaso muy concreto. En el peor, alguien propondrá un método nuevo, cada cual más complicado y difícil de interpretar que el anterior.
Y es que, aunque en principio usar superficies como “paisajes de estabilidad” puede parecer una buena idea, resulta no serlo. Los motivos últimos son sutiles, y requieren de herramientas con nombres tan poco atractivos como campo irrotacional o teorema del gradiente. Meterme en ese barrizal en un artículo de ecología hubiera sido de un mal gusto intolerable. Pero entonces, ¿cómo abordar el problema?
Aquí es dónde, por fin, el arte vino en mi ayuda. Imaginemos, me dije, un sistema dinámico con estas dos características:
- Tiene dos variables: nuestro punto (x,y) se mueve por un plano.
- Describe una oscilación: el punto describe una trayectoria cerrada, una y otra vez.
Tratemos ahora de imaginar una superficie tal que la bolita, en su constante descenso, dé vueltas y vueltas eternamente en una curva cerrada, sin dejar de rodar hacia abajo. ¿Qué aspecto tendría esa superficie? Intentemos imaginarla. A ojo, sin teoremas ni campos ni derivadas, ¡imaginación al poder! Y hete aquí que, por poder, podemos imaginarla. Y en gran medida, gracias a las extrañas superficies popularizadas por el artista M.C. Escher.
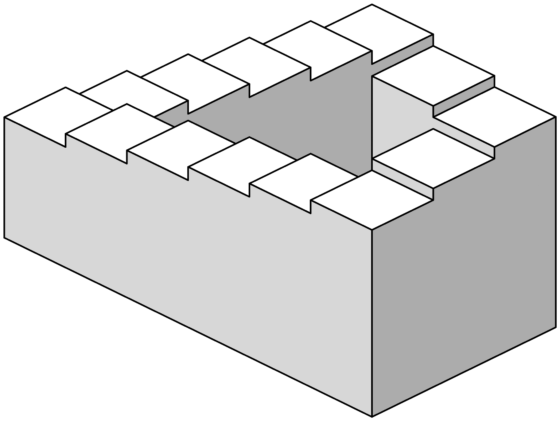
Podemos imaginarla, pero es una superficie que hace saltar todas nuestras alarmas. Algo tiene, algo le pasa, algo no cuadra, es una superficie… imposible. Y lo es, vaya si lo es. Resulta que desde el principio estábamos intentando pedirle peras al olmo. O subir las escaleras de Escher. ¡Con razón la cosa se ponía difícil!
¿Nada más?
Es posible que al lector más acostumbrado a la literatura científica el contenido de este post se le antoje corto para un artículo de investigación. Y llevará razón. El artículo original va más allá de lo que esta pequeña pieza de divulgación pretende (y debe) cubrir. Concretamente, añade un algoritmo para evaluar cuándo y dónde podemos usar estos paisajes de estabilidad en sistemas multidimensionales.
¿Algoritmo has dicho?, o sea, ¡que al final sí que te metiste en berenjenales matemáticos! En efecto… no me quedó más remedio. Diré en mi defensa que, esta parte, la de métodos, intenté hacerla lo más digerible posible. En este caso no fue el arte, sino la ingeniería de software quien vino en mi ayuda. Me explico: además de detallar cómo funciona el algoritmo, lo programé lo mejor que pude, lo empaqueté y lo puse pública y abiertamente a disposición de quien quiera usarlo, mejorarlo o incluso poner a prueba que lo que digo en mi artículo es correcto.
En mi opinión esto es una buena idea por muchos motivos. Además de los obvios (reproducibilidad, comodidad, …) también aporta una ventaja desde el punto de vista de la comunicación: permite a los lectores menos afines a las matemáticas utilizar el algoritmo sin necesidad de bucear demasiado en los detalles.
Para acabar, una reflexión suelta
Escribiendo este artículo tuve el raro honor de citar una publicación antiquísima, concretamente del año 1777. Cuando pensamos en investigación multidisciplinar, tendemos a dar por sentado que los «puentes» que quedan por tender entre disciplinas serán pocos y seguramente muy recientes. Sin embargo, queda claro que aún quedan puentes por tender, incluso, desde los fundamentos.
Y esta es la historia de mi artículo. La parte interesante. Creo. Es, en fin, lo que ningún editor de una revista académica aceptaría. Es también lo que le contaría a un amigo si me insistiese en que hablase del tema durante una cena o tomando unas cervezas.
Notas:
1 En esta otra entrada mostramos algunos ejemplos.
2 ¿Por qué casi?, pues porque el potencial mecánico se relaciona con la derivada segunda del estado, mientras que aquí estamos vinculando los “potenciales” a la derivada primera. Aún así, existe otra analogía mecánica, esta sí, impecable: el movimiento de una bolita en un potencial mecánico al sumergida en un medio viscoso.
Sobre el autor: Pablo Rodríguez Sánchez es doctor en matemáticas aplicadas e ingeniero de software de investigación en el Netherlands eScience Center (Amsterdam, Países Bajos)
