En mi anterior entrada del Cuaderno de Cultura Científica, titulada Exposiciones matemáticas en el metro de Bilbao (I), estuvimos hablando del Día Internacional de las matemáticas, del proyecto Marzo, mes de las matemáticas, realizado en colaboración con toda la comunidad matemática española y con la colaboración de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia e Innovación (FECYT), de las actividades que se están organizando dentro de este proyecto y de los excelentes e interesantes materiales que se están creando (a los cuales podéis acceder a través de la página web del proyecto), de cómo en el País Vasco (contando con el apoyo y colaboración de la Universidad del País Vasco/Euskal Herriko Unibertsitatea y el Basque Center for Applied Mathematics-BCAM, así como el Ayuntamiento de Bilbao y Metro Bilbao) se están organizando una serie de actividades, entre ellas, dos exposiciones matemáticas en el metro de Bilbao, Geometría Natural y Matemáticas para un mundo mejor, a la primera de las cuales dedicamos gran parte de la anterior entrada.

En esta entrada hablaremos de la otra exposición expuesta en el metro de Bilbao, que finalmente titulamos Matemáticas para un mundo mejor, aunque se podría haber titulado Sabías que … las matemáticas, puesto que surge a partir de las tarjetas matemáticas Sabías que desarrolladas dentro del proyecto Marzo, mes de las matemáticas.

Por lo tanto, empecemos hablando de la actividad de las tarjetas matemáticas. Mi compañero Pedro Alegría y yo mismo, asumimos la responsabilidad de la organización de la actividad de estas tarjetas. Primero montamos una comisión para la creación de los tres tipos de tarjetas matemáticas que habíamos planteado: Matemáticas + Literatura; Pasatiempos matemáticos; y ¿Sabías que…?. En esta comisión estabamos las siguientes personas: Marithania Silvero (Andalucía), José Muñoz Santuja (Andalucía), Julio Bernués (Aragón), Ignacio García (Canarias), Diego Alonso Santamaría (Castilla y León), Claudi Alsina (Cataluña), Dolores Gómez (Galicia), Pedro Alegría (responsable, País Vasco), Raúl Ibáñez (responsable, País Vasco), Alberto Magreñán (Rioja), Lara Orcos (Rioja), Manuel de León (Madrid), Alejandro Miralles (Valencia). A todas ellas quiero agradecerles su colaboración y el magnífico trabajo que han realizado.

La idea de esta actividad era la creación de una serie de materiales que podrían utilizarse como tarjetas para repartir, carteles para colocar en paredes o paneles de exposiciones, en función de las ideas que se desarrollasen en cada nodo del proyecto. Por ejemplo, en el País Vasco hemos impreso 15 tarjetas, de tamaño A5, de cada uno de los tres tipos (en castellano y euskera) para repartir en librerías, bares y comercios; hemos desarrollado la exposición Matemáticas para un mundo mejor en el metro de Bilbao, con algunas de las tarjetas del tipo ¿Sabías que…?; y vamos a realizar una exposición en la Biblioteca de Bidebarrieta (Bilbao) con algunas de las tarjetas del tipo Matemáticas + Literatura. O en Canarias se ha firmado un convenio con el Cabildo de Tenerife para mostrar las tarjetas en las pantallas del transporte público de la isla.

En el primer tipo de tarjetas matemáticas, que decidimos denominar Matemáticas + Literatura, se trataba de incluir en cada tarjeta una cita de una novela contemporánea en la que aparecieran reflejadas, de alguna forma, las matemáticas. Por ejemplo, en la siguiente imagen se muestra la tarjeta que lleva el título Las matemáticas ¿se inventan o se descubren? cuyo texto hemos extraído de la novela La fórmula preferida del profesor, de la escritora japonesa Yoko Ogawa.

Incluyo, a continuación, la cita:

—¿Qué especialidad de las matemáticas investigó usted en la universidad? —le pregunté, con la intención de hablar sobre algo relacionado con las matemáticas, en señal de agradecimiento por haber atendido a mi ruego y salido a la calle.

—Es un campo que suele llamarse la reina de las matemáticas —me comentó, después de un ruidoso trago de café—. Es tan hermoso como una reina, noble y al mismo tiempo cruel como un demonio. Es fácil de explicar en pocas palabras, pues son los números enteros que todo el mundo conoce. Estaba investigando la relación de los números 1, 2, 3, 4, 5, 6…

No esperaba que el profesor utilizara una palabra como “reina”, que parecía salida de un cuento. Se oía el ruido de una pelota de tenis botando a lo lejos […].

—¿Así que está usted descubriendo esa relación?

—Efectivamente, es un descubrimiento. No es una invención. Es como excavar y sacar de debajo de la tierra teoremas que ya existían mucho antes de que naciera, sin que nadie haya detectado su existencia. Es como transcribir línea tras línea una verdad que sólo está escrita en el cuaderno de Dios. Nadie sabe dónde está ese cuaderno ni cuándo se abre.

Al decir “teoremas que ya existían…”, señaló el punto en el espacio que siempre fijaba cuando estaba “pensando”.

Otro ejemplo es la tarjeta titulada Investigación policial versus investigación matemática, de la novela Los crímenes de Oxford, del escritor argentino Guillermo Martínez.

La cita contenida en esta tarjeta es la siguiente:

Hay una diferencia entre la verdad y la parte de verdad que puede demostrarse: ése es en realidad un corolario de Tarski sobre el teorema de Gödel – dijo Seldom-. Por supuesto, los jueces, los forenses, los arqueólogos, sabían esto mucho antes que los matemáticos. Pensemos en cualquier crimen con sólo dos posibles sospechosos.

Cualquiera de ellos sabe toda la verdad que interesa: yo fui o yo no fui. Pero la justicia no puede acceder directamente a esa verdad y tiene que recorrer un penoso camino indirecto para reunir pruebas: interrogatorios, coartadas, huellas digitales… Demasiadas veces las evidencias que se encuentran no alcanzan para probar ni la culpabilidad de uno ni la inocencia del otro. En el fondo, lo que mostró Gödel en 1930 con su teorema de incompletitud es que exactamente lo mismo ocurre en la matemática. El mecanismo de corroboración de la verdad que se remonta a Aristóteles y Euclides, la orgullosa maquinaria que a partir de afirmaciones verdaderas, de primeros principios irrebatibles, avanza por pasos estrictamente lógicos hacia la tesis, lo que llamamos, en una palabra, el método axiomático, puede ser a veces tan insuficiente como los criterios precarios de aproximación de la justicia. […] Gödel mostró que aun en los niveles más elementales de la aritmética hay enunciados que no pueden ser ni demostrados ni refutados a partir de los axiomas, que están más allá del alcance de estos mecanismos formales, enunciados sobre los que ningún juez podría dictaminar su verdad o falsedad, su culpabilidad o inocencia.

Las diecinueve tarjetas pertenecientes a la clase Matemáticas + Literatura las podéis encontrar en la página del proyecto Marzo, mes de las matemáticas, en concreto aquí.

Este es un material que se puede utilizar en diferentes formatos y lugares. Como tarjetas se pueden repartir en librerías (por ejemplo, se están repartiendo en algunas librerías de Bilbao, como la Librería Cámara o la Librería Louise Michel), en bibliotecas públicas (se están repartiendo tarjetas y colocando carteles en distintas bibliotecas de España), en centros culturales o en bares; como carteles pueden colocarse en medios de transporte, ya sea en el propio medio de transporte, en las instalaciones relacionadas o en las pantallas informativas en versión digital o en centros escolares; y son ideales como pósteres para una exposición (como la exposición que estamos organizando en la Biblioteca de Bidebarrieta y otras bibliotecas de Bilbao); o para todo lo que se nos pueda ocurrir, el límite es nuestra imaginación. Más aún, ese material, como el resto de materiales que se han subido a la página del proyecto Marzo, mes de las matemáticas, está ahí para que lo podáis utilizar.

En el segundo tipo de tarjetas matemáticas, que denominados Pasatiempos matemáticos, se trataba de incluir problemas de ingenio de diferentes dificultades. En una de las caras de la tarjeta se incluye el enunciado del pasatiempo matemático, acompañado de una ilustración, mientras que en la otra cara se incluye información relacionada con ese pasatiempo matemático. Por ejemplo, en las siguientes imágenes vemos un problema de ingenio cuyo título es Aquí hay gato encerrado.

El enunciado del problema Aquí hay gato encerrado, es el siguiente:

Hay 5 cajas numeradas del 1 al 5. Cada noche el gato duerme en una caja adyacente a la de la noche anterior. Cada mañana puedes abrir una caja y mirar si el gato está dentro. ¿Cuántos días necesitas para asegurarte de encontrar al gato?

Y el comentario que aparece en la otra cara es:

Este pasatiempo pertenece a la familia de problemas de tipo persecución-evasión (como el juego policías y ladrones), que son aquellos en los cuales un grupo –en este caso quien juega– intenta localizar a los miembros de otro grupo –el gato– en un entorno cerrado –las cinco cajas–. El rompecabezas fue presentado en 1999 por dos matemáticos rusos en el entorno de las olimpiadas matemáticas, aunque el estudio matemático de los problemas persecución-evasión se remonta a la década de 1970. En 2014 este pasatiempo se hizo famoso a raíz de su aparición, en una versión más general, en el periódico New York Times.

Sobre este problema en concreto escribí no hace mucho en el Cuaderno de Cultura Científica, podéis leer la entrada aquí: Buscando una matemática en el castillo.

Las diecinueve tarjetas pertenecientes a la clase Pasatiempos matemáticos las podéis encontrar en la página del proyecto Marzo, mes de las matemáticas, en concreto aquí. Además, ahí mismo podéis encontrar las soluciones a los diferentes pasatiempos.

De nuevo, este es un material que se puede utilizar en diferentes formatos y lugares. Por mencionar un par de ejemplos, en Bilbao estamos repartiéndolas en diferentes bares, librerías y comercios o en Tenerife se están mostrando en las pantallas del transporte público.

El problema que aparece en esa pantalla de La Laguna es Con todas las cifras, que dice así:

Con todas las cifras, del 1 al 9, en orden creciente, intercalar los signos «+» y » –» de forma que el resultado de la operación sea 100. Por ejemplo, 1 + 2 + 3 – 4 + 5 + 6 + 78 + 9 = 100.

El tercer tipo de tarjetas es el denominado ¿Sabías que?, que recoge aplicaciones, más o menos actuales, de las matemáticas. Por ejemplo, en la siguiente imagen se incluyen las dos caras de la tarjeta ¿Sabías que … tus deportivas se diseñan utilizando matemáticas?.

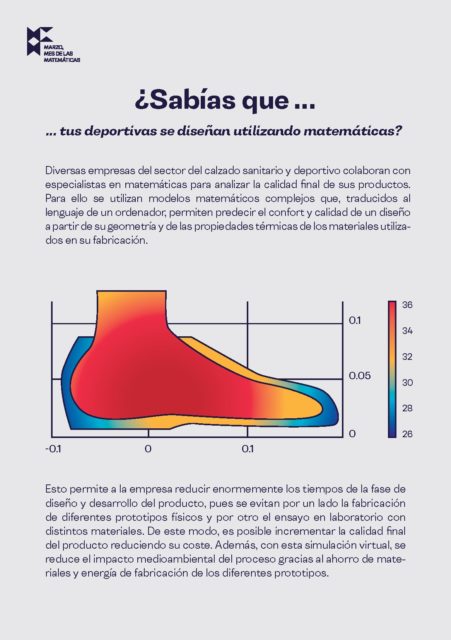
El texto de esta tarjeta es el siguiente:

Diversas empresas del sector del calzado sanitario y deportivo colaboran con especialistas en matemáticas para analizar la calidad final de sus productos. Para ello se utilizan modelos matemáticos complejos que traducidos al lenguaje de un ordenador permiten predecir el confort y calidad de un diseño a partir de su geometría y de las propiedades térmicas de los materiales utilizados en su fabricación.

Esto permite a la empresa reducir enormemente los tiempos de la fase de diseño y desarrollo del producto, pues se evitan por un lado la fabricación de diferentes prototipos físicos y por otro el ensayo en laboratorio con distintos materiales. De este modo, es posible incrementar la calidad final del producto reduciendo su coste. Además, con esta simulación virtual, se reduce el impacto medioambiental del proceso gracias al ahorro de materiales y energía de fabricación de los diferentes prototipos.

El texto de esta tarjeta está basado en una investigación de los profesores J. Durany, L. Poceiro y F. Varas, de la Universidad de Vigo, a quienes agradecemos su generosidad. Además, quien quiera saber más sobre el tema puede leer este artículo.

Las dieciocho tarjetas pertenecientes a la clase ¿Sabías que…? las podéis encontrar en la página del proyecto Marzo, mes de las matemáticas, en concreto aquí. Y una vez más, este es un material que se puede utilizar en diferentes formatos y lugares. El ejemplo que traemos a esta entrada del Cuaderno de Cultura Científica son los paneles de la exposición Matemáticas para un mundo mejor, que se puede ver en el metro de Bilbao.

Finalmente, el diseño de las tarjetas matemáticas es un magnífico trabajo de la diseñadora canaria Carla Garrido.

Antes de empezar con la exposición del metro de Bilbao me gustaría dar las gracias a los profesores Jose Ignacio Royo y Alex Aginagalde por traducir al euskera los textos de las tarjetas.

Empezaremos por el panel de presentación de la exposición, que fue colocada en la estación de metro Moyua del metro de Bilbao el pasado 1 de marzo, que podéis ver en la siguiente imagen.

El texto de ese panel de presentación es el siguiente:

Esta exposición, cuyo título corresponde al lema elegido para conmemorar el Día Internacional de las Matemáticas del año 2021, ofrece un pequeño recorrido por algunas cuestiones relacionadas con aplicaciones actuales de las matemáticas al mundo que nos rodea, en áreas tan diversas como la industria, ingeniería, tecnología, sanidad, economía y deporte.

Empecemos nuestro paseo por la exposición Matemáticas para un mundo mejor, que físicamente estará en la estación de Moyua de Metro Bilbao durante el mes de marzo y en la estación de Portugalete durante el mes de abril, por el panel ¿Sabías que … se puede cambiar la válvula aórtica usando matemáticas?.

El texto que acompaña a este panel, que es una versión reducida del texto de la correspondiente tarjeta y que está basado en una investigación de Marcos Loureiro, de la Universidade de Vigo (más información en la página web de Marcos Loureiro), es el siguiente:

La estenosis aórtica es una enfermedad que provoca un funcionamiento incorrecto de esa válvula coronaria, obligando en casos graves a su recambio. Además de la operación a corazón abierto, se puede cambiar la válvula accediendo a los órganos interiores a través de un catéter (técnica TAVI).

Gracias a técnicas de simulación numérica es posible realizar virtualmente varias TAVI a un mismo paciente. Así pueden predecirse posibles complicaciones durante la intervención, modificaciones en la válvula o las tensiones a las que estará expuesto el anillo aórtico durante el procedimiento.

Otro de los paneles de la exposición es ¿Sabías que … Suiza ganó la Copa América de vela gracias al uso de las matemáticas?, cuyo texto recoge una investigación dirigida por el matemático italiano Alfio Quarteroni (Politecnico di Milano, Italia y EPFL, Suiza) y sobre la que podéis más en la página de Alfio Quarteroni.

El texto de este panel es el siguiente:

Hace pocos años, la manera de probar el rendimiento de un barco era exponerlo a situaciones de flujo realistas en túneles de viento. Utilizando modelos matemáticos se puede simular en un ordenador la respuesta del barco bajo distintas condiciones. Por ejemplo, se puede mejorar el diseño del yate para que navegue con la menor resistencia posible u obtener nuevas formas de velas que interactúen mejor con el aire, o crear modelos para ayudar al navegante a tomar decisiones. Estas técnicas se aplicaron al barco suizo Alinghi, que ganó la Copa América en 2003 y 2007.

Otro de los paneles es ¿Sabías que … multitud de paisajes de películas se generan por ordenador usando fractales?

El texto de este panel es:

Los fractales son objetos matemáticos cuya estructura se repite a distintas escalas o que son extremadamente rugosos. Tienen aplicaciones en medicina, biología, geología, telecomunicaciones, economía o compresión de imágenes digitales, entre otras. Han sido utilizados incluso en el cine, como en Star Trek 2: La ira de Khan (1982) para generar un paisaje realista, en Guardianes de la galaxia, vol. 2 (2017) para crear el planeta de Ego o en Aniquilación (2018) para representar a un alienígena.

Otro interesante panel de la exposición es el que corresponde al tema ¿Sabías que … escuchas música gracias a la transformación matemática de los sonidos?

Y el texto del panel es el siguiente:

Cuando se graba digitalmente música, los sonidos se descomponen en frecuencias (notas musicales) y amplitudes (volumen). Los sonidos se transforman y almacenan como un listado de números. Esa transformación, llamada transformada de Fourier, permite distintas manipulaciones sobre la señal (el listado de números almacenados): comprimirla, filtrarla, quitar ruidos, añadir efectos, elaborar apps de reconocimiento de canciones, etc. Luego la operación inversa de la transformada permite su reproducción en cualquier dispositivo digital.

Otro panel basado en una investigación actual es ¿Sabías que … las matemáticas son fundamentales en la predicción de tsunamis?, en concreto, la investigación del grupo EDANYA de la Universidad de Málaga, a quienes agradecemos su colaboración.

Cuyo texto, reducido del texto de la tarjeta correspondiente como en los demás paneles, es:

Las matemáticas son la base de los modelos usados para la simulación numérica de flujos geofísicos. A partir de datos precisos del terreno, estos modelos muestran desde la inundación que puede producir el desbordamiento de un río hasta la dinámica del mar de una zona costera. Incluso pueden predecir el tiempo de impacto de una onda de tsunami y la altura con que la ola va a alcanzar la costa. Para ello combinan algoritmos numéricos y hardware gráfico que simulan el tsunami y sus efectos en pocos minutos; así dotan a las autoridades de importantes herramientas de prevención.

E incluimos un panel más como muestra de esta exposición, el panel ¿Sabías que … los nudos pueden ayudar a curar enfermedades?

Cuyo texto es el siguiente:

El ADN es la molécula que almacena nuestro código genético. Consiste en dos cadenas que se enrollan en forma de doble hélice y una serie de “peldaños” que las conectan. A veces el ADN está superenrollado, lo que hace difícil que tengan lugar ciertos procesos indispensables para la vida, aunque el organismo dispone de topoisomerasas, enzimas que manipulan y desenredan las cadenas. La teoría matemática de nudos ayuda a entender la acción de estas enzimas y a decidir cómo llevar el ADN a su estado normal.

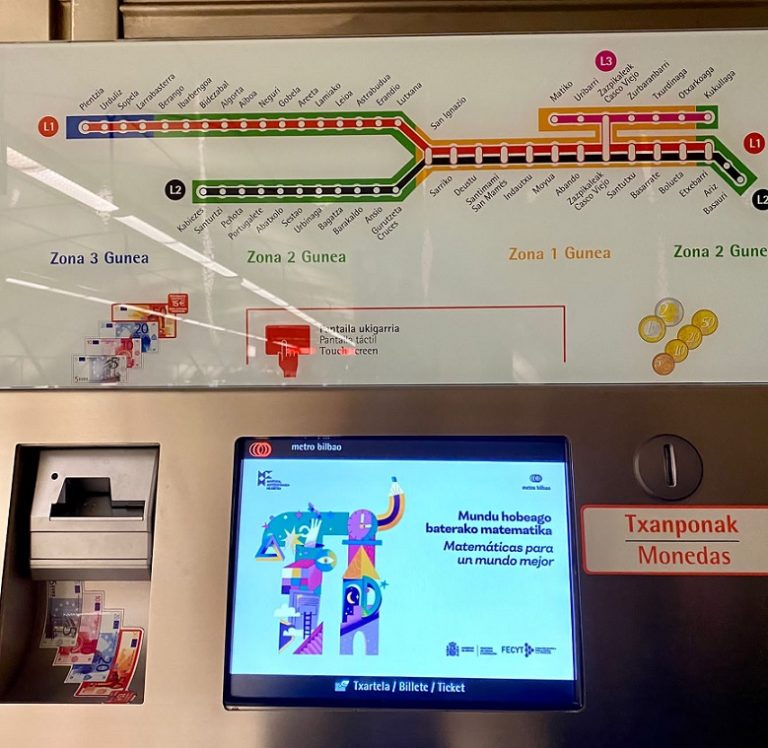
Terminamos con la imagen que durante unos días ha estado colocada en las máquinas expendedoras de Metro Bilbao, anunciando las exposiciones.

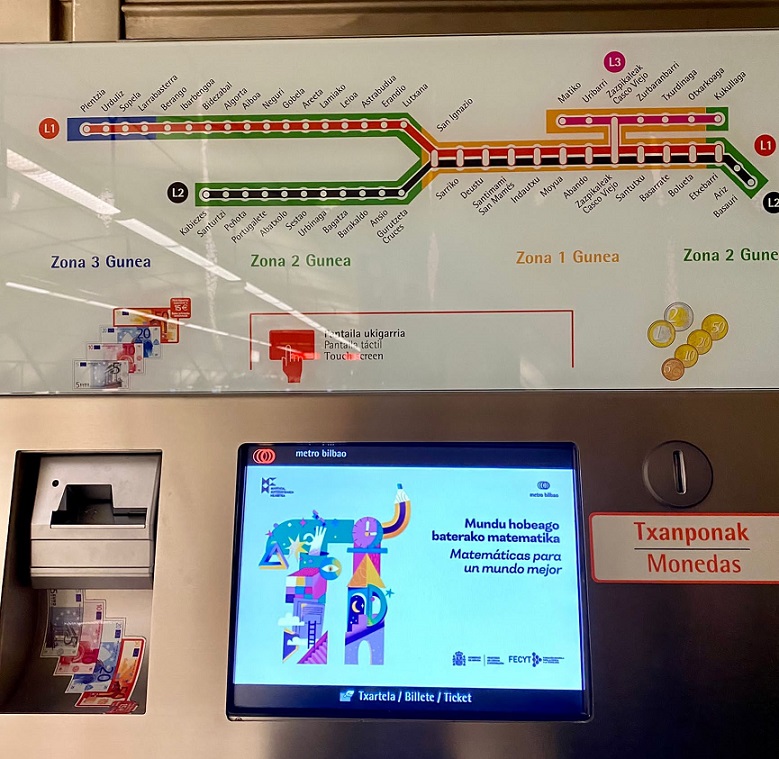
Para terminar, una vez más, agradecer a Metro Bilbao que haya colaborado con el proyecto Marzo, mes de las matemáticas y que nos haya brindado la oportunidad de realizar estas dos exposiciones, Geometría Natural y Matemáticas para un mundo mejor, en un espacio tan especial como son las estaciones del metro.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica