En el primer capítulo de mi libro Del ajedrez a los grafos, la seriedad matemática de los juegos, cuyo título era Pensamiento matemático, abordaba diferentes estrategias para la resolución de problemas matemáticos, así como la obtención de estrategias ganadoras en diferentes juegos. Una de las herramientas que quedó fuera en la versión final del libro fue la utilización de la simetría, que hoy abordaremos en esta entrada del Cuaderno de Cultura Científica.

La simetría es una herramienta muy útil en las demostraciones matemáticas, en la resolución de problemas, incluidos los juegos de ingenio, y en la obtención de estrategias ganadoras en los juegos de competición.
Aunque cuando hablamos de estrategias ganadoras basadas en la simetría en este contexto solemos referimos a que uno de los dos jugadores, normalmente el segundo, realiza movimientos simétricos a los del jugador rival. En esta entrada vamos a mostrar y analizar dos juegos sencillos, la margarita y bloqueado.
La margarita es un juego para dos personas que se juega con un cierto número de fichas, por ejemplo, dieciséis, formando una circunferencia, como muestra la siguiente imagen. Los jugadores, por turnos, deberán retirar o bien una ficha o bien dos, pero en tal caso que estén una junto a la otra, sin hueco entre ellas. Gana el jugador que retira la última ficha.

Inspirado en el conocido juego infantil “me quiere, no me quiere” mientras se deshoja una margarita, fue inventado por el matemático recreativo y ajedrecista estadounidense Sam Loyd (1841-1911) a finales del siglo XIX. Publicó este juego en 1896 en su columna de rompecabezas del periódico The Brooklyn Daily Eagle, y posteriormente, en la revista británica Tits-Bits en 1897.

Sam Loyd es uno de los grandes de la matemática recreativa. No solo creaba rompecabezas o problemas de ingenio, o adaptaba algunos ya existentes (con polémicas incluidas sobre su autoría), sino que los vestía con una narrativa fantástica y cautivadora, o los acompañaba de toda clase de trucos publicitarios, como la creación de impactantes premios (un ejemplo fueron los 1.000 dólares que ofreció a quien resolviera el rompecabezas 14-15, que acabaría alcanzando una gran popularidad).
Durante la educación secundaria se aficionó al ajedrez y a la creación de problemas para este juego. Después empezó a estudiar ingeniería, pero descubrió que se podía vivir de la creación de rompecabezas matemáticos y problemas de ajedrez. A lo largo de su vida realizó trabajos muy variados, como contratista de fontanería, grabador de madera, caricaturista o compró una cadena de tiendas de música, pero sobre todo dedicó su tiempo a la creación y publicación de problemas de ingenio.
Escribió columnas en periódicos y revistas, como The Brooklyn Daily Eagle, Tits-Bits (donde colaboró con el británico Henry E. Dudeney) o Scientific American, y editó sus propias revistas, como Sam Loyd’s puzzle magazine.
Entre sus rompecabezas más famosos están el problema de los burros, el puzzle 14-15, de regreso a Klondike o Fuera de la Tierra. Tras su muerte, su hijo publicaría su libro Sam Loyd’s Cyclopedia of 5000 Puzzles, Tricks and Conundrums with Answers (1914).

La margarita, también conocido con el nombre la cadena, admite una estrategia ganadora para el segundo jugador basada en la simetría. Si el jugador que inicia la partida retira una ficha (respectivamente, dos), la respuesta del otro jugador será retirar la ficha (respectivamente, las dos fichas) que está en la posición diametralmente opuesta en la circunferencia, generando así dos partes aisladas simétricas (para la margarita de dieciséis fichas, o cualquier cantidad par de fichas).
A partir de la posición inicial de las fichas del juego, como en la imagen que está más arriba, mostramos la primera jugada de los dos jugadores, si el primero quita una de las fichas y el segundo la diametralmente opuesta, quedando efectivamente dos partes aisladas con la misma cantidad de fichas.


A partir de ese momento, el segundo jugador aplicará la simetría, retirando en cada movimiento las mismas fichas que haya quitado el primero, pero en la parte contraria a la de su oponente. Mostramos las siguientes jugadas del juego iniciado en las anteriores imágenes. Si el primer jugador quita dos fichas de la parte derecha, como muestra la imagen.

El segundo jugador quitará las dos en la parte contraria.

Y así con las demás jugadas, en las que el segundo jugador quita las fichas simétricas a las retiradas por el primer jugador, de manera que así se asegura que será este jugador el que será el último en retirar fichas.






Si el juego empieza con un número impar de fichas, el primer movimiento del segundo jugador consistirá en retirar una cantidad distinta de fichas a la del primer jugador, dos si este ha quitado una y una si han sido dos, con el objetivo de dejar de nuevo las fichas restantes divididas en dos partes simétricas aisladas.
Bloqueado es otro juego para dos personas cuya estrategia ganadora está basada en la simetría. El tablero, que puede pintarse sobre una hoja de papel o construirse con más encanto en madera, consta de dos filas de 10 casillas contiguas. Al iniciarse la partida, cada jugador dispondrá de dos fichas colocadas en un extremo de las dos filas, como se muestra en la imagen.

Las reglas del juego son las siguientes:
i) cada jugador mueve, por turnos, una de sus fichas, con las que avanzará (hacia la derecha o izquierda, dependiendo de su posición inicial), o retrocederá, tantas casillas como desee, sin saltar por encima de las fichas del contrario;
ii) gana el jugador que consiga que su oponente quede bloqueado, es decir, que no pueda mover ninguna de sus dos fichas.
Más allá de las reglas, será jugando cuando nos percataremos de cómo funciona el juego. Una de las primeras observaciones que podemos hacer es que, si un jugador cierra una de las filas, el otro deberá cerrar la otra, obligándole al primero a retroceder hasta que quede bloqueado

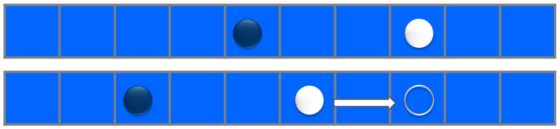
Luego la estrategia es obligar al jugador contrario a que cierre una fila, evitando a su vez ser quien la cierra primero. Así, si un jugador (fichas oscuras en la imagen de abajo) cierra una de las filas, el otro jugador (fichas blancas) cerrará inmediatamente la otra fila, obligando a su rival a retroceder movimiento a movimiento hasta quedar bloqueado, y perder.

En este juego, existe una estrategia ganadora para el segundo jugador que consiste en no ser el primero en cerrar alguna de las filas y obligar al adversario a hacerlo. Pero, ¿cómo conseguirlo? La clave está, de nuevo, en la simetría.
Para evitar bloquear una de las líneas, el segundo jugador deberá conseguir en cada movimiento que la distancia entre fichas –el número de casillas que las separan- en las dos filas sea la misma (distancia de simetría), así no cerrará ninguna fila, salvo cuando cierre las dos. Por otra parte, será el primer jugador quien rompa la simetría en cada movimiento.
Y para forzar al primer jugador para que sea quien cierre primero una de las dos filas el segundo jugador deberá conseguir que la distancia de simetría entre las fichas sea cada vez más pequeña. Esto va a ser posible ya que cuando el primer jugador rompe la simetría pueden ocurrir dos cosas:
i) si ha hecho avanzar una de sus fichas (las fichas oscuras hacia la derecha, las blancas hacia la izquierda), la distancia ahora entre las fichas de esa fila será más pequeña que la distancia de simetría anterior, con lo cual el segundo jugador podrá mover su ficha en la otra fila para disminuir la distancia de simetría;
ii) si ha retrocedido una de sus fichas, de forma que la distancia entre las fichas de esa fila sea mayor que la distancia de simetría, el segundo jugador avanzará su ficha en esa fila para mantener la distancia de simetría, con la diferencia de que al retroceder el primer jugador va perdiendo terreno, casillas para mover, y llegará el momento que no tendrá más opción que cerrar una de las filas, y perderá.
Una variante de este juego consiste en que las longitudes de las filas sean distintas. ¿Sigue siendo válida la estrategia ganadora?

Bibliografía
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, RBA, 2015.
2.- Sam Loyd’s Cyclopedia of 5000 Puzzles, Tricks and Conundrums with Answers [http://www.mathpuzzle.com/loyd/], publicado en 1914.
3.- Luis Ferrero, El juego y la matemática, Ed. La Muralla, 2001.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Horacio
Hola Raúl,
Enhorabuena por el artículo.
He estado buscando tu libro Del ajedrez a los grafos, pero imagino que, no solo está más que descatalogado, si no que es imposible conseguirlo en cualquier sitio.
¿Hay alguna manera de hacerme con el libro?
Muchas gracias