Un grupo de N estudiantes de lógica se somete a una prueba para verificar sus habilidades en esta materia. Deben situarse en fila mirando hacia la derecha. Sin que ellos puedan verlo, se coloca al azar un sombrero rojo o azul sobre cada cabeza.

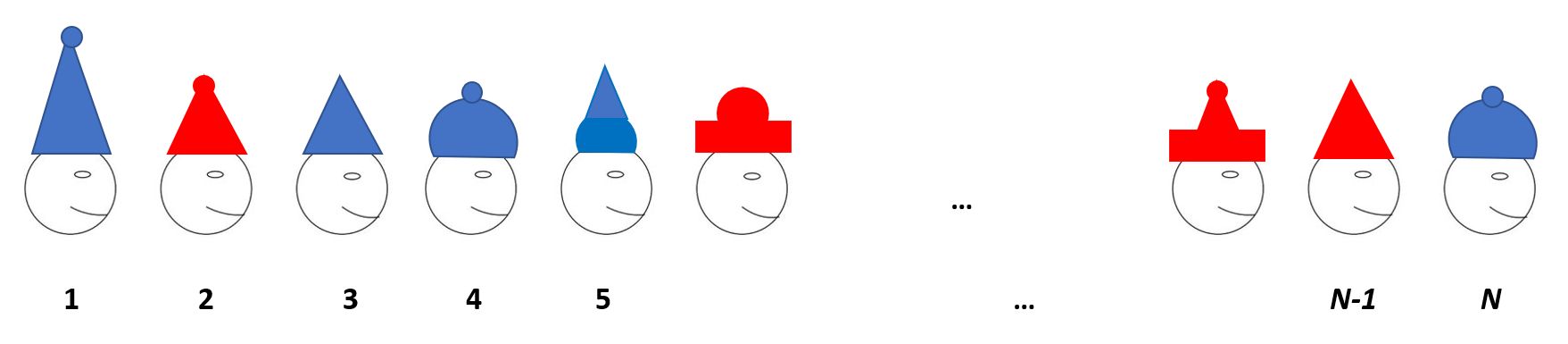
El estudiante situado más a la izquierda (en la posición 1) puede ver todos los gorros menos el suyo. El compañero situado delante de él (en la posición 2) divisa todos los sombreros excepto el suyo y el del estudiante colocado detrás de él (en la posición 1). En general, la persona situada en la posición k puede ver (solo) los gorros de sus compañeros colocados en los lugares k+1, k+2, etc. hasta N.

A cada estudiante se le preguntará por el color que piensa que tiene su sombrero. Tras finalizar esta ronda de preguntas y respuestas, se entregará al grupo tantas tablets como el número de aciertos. El propio grupo se encargará después de repartir “su botín”. Es decir, a los estudiantes les interesa colaborar.

Antes de ponerse en fila, los estudiantes pueden pactar una estrategia para responder a la pregunta de manera más certera. Pero, una vez colocados en línea, los sombreros se colocan al azar y los estudiantes ya no pueden interactuar. Las preguntas y las respuestas se realizarán en voz alta. Se empezará interrogando al estudiante más a la izquierda (en la posición 1) y se continuará en orden hasta terminar con el situado más a la derecha (en la posición N).

Buscando una buena estrategia

Si los estudiantes responden al azar ganarán, en media, N/2 tablets ya que la probabilidad de acertar de ese modo es de 1/2.

Bertrand, uno de los estudiantes del grupo, propone el siguiente método de juego:

· El estudiante 1 (el situado más a la izquierda) responderá diciendo el color del gorro del estudiante 2, que de este modo conocerá de manera certera el color de su sombrero.

· El estudiante 2 repetirá lo que le ha dicho el jugador 1 y, por lo tanto, acertará.

· El estudiante 3 responderá diciendo el color del gorro del estudiante 4.

· El estudiante 4 repetirá lo que le ha dicho el estudiante 3, y por lo tanto ganará.

Y siguen respondiendo de este modo. Esta manera de proceder garantiza al menos N/2 respuestas exactas. Además, en media, los estudiantes responderán correctamente 3N/4 (= N/2 + N/4) veces, ya que las personas colocadas en lugares impares acertarán (por azar) aproximadamente una de cada dos veces.

La mayor parte de los estudiantes, convencidos, aplauden la estrategia de Bertrand. Sin embargo, Helena —una “fuera de serie” en lógica— está en desacuerdo. Y dice a sus compañeros: «Tengo otra idea mejor. Con ella ganaremos todos una tablet… salvo quizás uno de nosotros».

¿Cuál puede ser la estrategia de Helena? Piensa un poco antes de mirar la respuesta propuesta…

La estrategia de Helena

Helena (ver [2]) propone que cada persona del grupo debe transmitir información sobre la paridad (par o impar) del número de sombreros rojos colocados a partir de él (contando su sombrero). Es decir, la forma de actuar es la siguiente:

• El estudiante 1 (el situado más a la izquierda) dice “rojo” como respuesta al color de su sombrero si el número de gorros rojos que ve es par y contesta con azul en caso contrario. Tiene una posibilidad sobre dos de acertar.

• Si el estudiante 2 ve que a partir de él hay una cantidad de gorros rojos de la misma paridad que la indicada por el estudiante 1 (recordemos que las respuestas se dan en voz alta), sabe que él tiene un gorro de color azul. Y si la paridad no coincide, sabe que su gorro es de color rojo. Responde siguiendo la estrategia de Helena, así que su respuesta es necesariamente correcta.

• El estudiante colocado en el lugar 3 conoce la paridad de los sombreros rojos desde el 2 hasta el N (por la información dada por su colega situado en la posición 1) y sabe si el estudiante 2 tiene un gorro rojo o azul (ya que ha oído su respuesta y todos saben que es la correcta). Así, conoce la paridad del número de sombreros rojos desde el 3 hasta el N. Como ve todos los gorros desde el 4 hasta el N, deduce el color de su sombrero sin temor a equivocarse.

El proceso continúa de este modo respondiendo cada estudiante turno por turno. Todos, excepto quizás el primero, dan la respuesta correcta. ¡Así que Helena tenía razón! Con su estrategia ganarán al menos N-1 tablets…

En el peor de los casos, quedaría por decidir quien se queda sin tablet… pero esa es otra historia.

Referencias

[1] Jean-Paul Delahaye, Rubrique des paradoxes: Les chapeaux alignés, Accromath. Volume 15.1 – hiver-printemps 2020

[2] Jean-Paul Delahaye, Solution du paradoxe précédent: Les chapeaux alignés, Accromath. Volume 15.2 – été-automne 2020

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad