El matemático y lógico inglés John Venn (1834-1923) nació un 4 de agosto. Es fundamentalmente conocido por su famoso método de representación gráfica conocida como diagramas de Venn.

Profesor en la Universidad de Cambridge, publicó tres textos sobre lógica, su área de mayor interés: The Logic of Chance (1866), Symbolic Logic (1881) –en el que introdujo los diagramas de Venn– y The Principles of Empirical Logic (1889). En 1883, fue elegido miembro de la prestigiosa Royal Society.
El 4 de agosto de 2014, con motivo del 180 aniversario de su nacimiento, Google le dedicó un divertido Doodle interactivo con el que se puede jugar encontrando intersecciones entre diferentes conjuntos.

Vamos a usar precisamente diagramas de Venn para resolver el siguiente juego de lógica.
Los plinks,los plonks y los plunks son los miembros de tres sociedades científicas. Se sabe que todos los plinks son plonks y que algunos plunks son plinks. ¿Cuál de las siguientes afirmaciones es cierta?
1. Todos los plinks son plunks.
2. Algunos plonks son plunks.
3. Algunos plinks no son plunks.
Para solucionar este problema, recurrimos a un diagrama de Venn que representa los tres conjuntos –el de los plinks en azul, el de los plonks en rojo y el de los plunks en verde–en el que aparecen indicadas las distintas regiones del diagrama con las letras A, B, C, D y E.
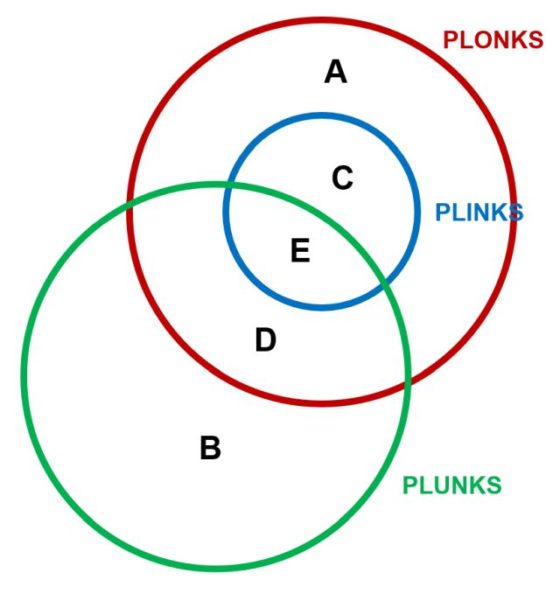
-
A es el conjunto de los que son plonks que no son ni plinks ni plunks.
-
B es el conjunto de los que son plunks que no son plonks (y, por lo tanto, tampoco plinks).
-
C es el conjunto de los que son plinks que no son plunks.
-
D es el conjunto de los que son plonks y plunks que no son plinks.
-
E es el conjunto de los que son plinks, plonks y plunks a la vez.
Observar que el conjunto de los plinks es la unión de C y E, el conjunto de los plonks es la unión de A, C, D y E (es decir, la unión del conjunto de los plinks con A y D; recordar que todos los plinks son plonks) y el conjunto de los plunks es la unión de B, D y E. Alguna de las zonas A, B, C, D y E podría ser vacía (desconocemos este dato de momento) con lo que el diagrama de Venn podría cambiar su forma.
Se nos dice que “todos los plinks son plonks” –ya hemos usado esta información a la hora de dibujar el diagrama de Venn– y que “algunos plunks son plinks”, de donde se deduce que la región E no puede ser vacía.
Analicemos ahora las tres afirmaciones cuya veracidad o falsedad debemos decidir.
1. Todos los plinks son plunks.
Si la afirmación 1. fuera cierta, la región C sería vacía. Pero desconocemos lo que sucede con la región C, por lo que, de momento, no podemos concluir si esta afirmación es cierta o falsa.
2. Algunos plonks son plunks.
La declaración 2. dice que la unión de las regiones E y D no puede ser vacía. Ya sabemos que la región E es no vacía, por lo que esta afirmación es cierta.
3. Algunos plinks no son plunks.
La afirmación 3. implica que la región C es no vacía. Pero desconocemos lo que sucede en la región C, por lo que, de momento, no podemos concluir si esta afirmación es cierta o falsa.
Por tanto, con los datos que tenemos, la única afirmación que con toda seguridad es verdadera es la 2. Para que 1. fuera cierta, la zona C no debería tener elementos. Y para que 3. fuera cierta, esta región C debería ser no vacía. Así que una, y solo una, de las afirmaciones 1. y 3. es verdadera; pero no sabemos cuál es. Por cierto, con los datos proporcionados, desconocemos si las zonas A, B, C y D son o no vacías.
Referencia:
Euphony, Futility Closet, 27 octubre 2020
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

Celebrando a John Venn con un juego de ló…
[…] El matemático y lógico inglés John Venn (1834-1923) nació un 4 de agosto. Es fundamentalmente conocido por su famoso método de representación gráfica conocida como diagramas de Venn. Profesor en la Universidad de Cambridge, publicó tres textos sobre lógica, su área de mayor interés: The Logic of Chance (1866), Symbolic Logic (1881) –en el que introdujo los diagramas … […]